Playing with Generative Flow Matching Model
Previously, we were playing with score-based diffusion model, which generates data from noise prior by predicting the scores, \(\nabla_x\log p(x)\), and trained using forward SDE. Flow-based model, on the other hand, generates the data by predicting the flow vector fields that warps any prior distribution to the unknown data distribution and is a more general formalism and easier to train in practice. I will explore flow matching in 2 parts, continuous and discrete.
In the continuous case, flow matching model aims to construct a time-dependent vector field \(v: [0, 1] \times \mathbf{R}^d \to \mathbf{R}^d\) to reshape a simple (or known sample-able) prior distribution \(p_0\) into a more complicated and unknown distribution \(p_1\). Typically, \(p_0\) and \(p_1\) are noise and data distributions respectively but \(p_0\) can actually be any prior. We let \(p_t(x)\) be the probability density path at time \(t\) and \(u_t(x)\) be the corresponding vector field, which generates \(p_t(x)\). Once we know \(u_t(x)\), we can generate a sample from prior \(x_0\), use \(u_0(x_0)\) to find \(x_t\) and use \(u_t(x_t)\) to find \(x_{2t}\) etc until we recover the data \(x_1\). So the flow matching objective is
\[\mathcal{L}_{FM}(\theta) = \mathbf{E}_{t,p_t(x)}||v_{t, \theta}(x) - u_t(x)||^2\]where \(v_{t, \theta}(x)\) is a neural network regressing on the flow vector field \(u_t(x)\) at all time \(t\).
We don’t have a close form of \(u_t\) but we can construct \(p_t\) and \(u_t\) per sample \(x_1 \sim q(x_1) \sim p_1\) (conditioned on a data sample), i.e. the conditional probability path \(p_t(x|x_1)\) will satisfy the following conditions at the boundaries of time: \(t=0\) and \(t=1\)
- \[p_0(x|x_1) \sim \text{prior or noise} \sim p_0(x) \sim \mathcal{N}(x|0, I)\]
- \[p_1(x|x_1) \sim \delta(x_1) \sim \mathcal{N}(x|x_1, \sigma^2I), \sigma\approx0\]
From these conditional probability endpoints, we can construct conditional probability path \(p_t(x|x_1)\) and conditional vector field \(u_t(x|x_1)\). The conditional flow matching objective is then
\[\mathcal{L}_{CFM}(\theta) = \mathbf{E}_{t, q(x_1), p_t(x|x1)}||v_{t,\theta}(x) - u_t(x|x_1)||^2\]where \(v_{t, \theta}(x)\) is a neural network. Previous work has shown that these 2 objectives or loss functions are equivalent in the sense that optimizing them will result in the same weight, or they have the same gradient, i.e.
\[\nabla_\theta \mathcal{L}_{FM}(\theta) = \nabla_\theta \mathcal{L}_{CFM}(\theta)\]At training time, given \(p_0\) and training data from \(p_1\), we do the following:
- Sample \(t\in[0, 1]\)
- Sample data point \(x_1\sim p_1(x) \sim q(x)\)
- Sample \(x \sim p_t(x \mid x_1)\)
- Compute corresponding conditional vector field \(u_t(x \mid x_1)\)
- Use neural network \(v_{t,\theta}(x)\) to regress on the conditional vector field.
So what is this conditional probability path \(p_t(x \mid x_1)\) and conditional vector field \(u_t(x \mid x_1)\)?
The conditional flow matching objective works with ANY choice of conditional path and conditional vector field. One way to construct \(p_t(x \mid x_1)\) is to use Gaussian distribution with time-varying mean and variances:
\[p_t(x \mid x_1) = \mathcal{N}(x \mid \mu_t(x_1), \sigma_t(x_1)^2 I)\]where \(\mu_t(x_1)\) satisfies
\[\begin{align*} \mu_0(x_1) = 0 \\ \mu_1(x_1) = x_1 \end{align*}\]and \(\sigma_t(x_1)\) satisfies
\[\begin{align*} \sigma_0(x_1) = 1 \\ \sigma_1(x_1) = \sigma_{min} \end{align*}\]And the unique vector field we are trying to regress to is
\[u_t(x \mid x_1) = \frac{\sigma'_t(x_1)}{\sigma_t(x_1)}[x - \mu_t(x_1)] + \mu'_t(x_1)\]If we choose or design the conditional probability path to be Gaussian, then we can easily sample \(p_t(x \mid x_1)\) and \(u_t(x \mid x_1)\) will have exact form. Other formulations of \(p_t(x \mid x_1)\) will also work but might not have easy-to-compute \(u_t(x \mid x_1)\). Let’s look at some examples.
Example 1: Diffusion Conditional Vector Fields
In the previous diffusion post, I looked into the variance exploding (VE), variance preserving (VP) and sub-VP SDEs, mapping from data to noise distributions.
- VE conditional path
For VE, we kept adding noise until the signal got destroyed:
\[p_t(x|x_1) = \mathcal{N}(x|x_1, \sigma_{1-t}^2I)\]The conditional vector field is then
\[u_t(x|x_1) = -\frac{\sigma'_{1-t}}{\sigma_{1-t}}(x-x_1)\]- VP conditional path
For VP, while addiing noise, we also attenuate the signal:
\[p_t(x|x_1) = \mathcal{N}(x|\alpha_{1-t}x_1, (1 - \alpha_{1-t}^2)I)\]The conditional vector field is then:
\[u_t(x|x_1) = \frac{\alpha_{1-t}'}{1 - \alpha_{1-t}^2}(\alpha_{1-t}x - x_1)\]Note that this \(\alpha_t\) is decreasing with time \(t\) and parametrized by \(\beta(s)\):
\[\alpha_t = e^{-\frac{1}{2}\int_0^t\beta(s)ds}\]Example 2: Optimal Transport Conditional Vector Fields
One natural choice for this conditional probability path is to to define mean and std to be linear in time:
\[\mu_t(x|x_1) = tx_1\] \[\sigma_t(x|x_1) = 1 - (1 - \sigma_{min})t\]The the conditional vector field is then:
\[u_t(x|x_1) = \frac{x_1 - (1 - \sigma_{min})x}{1 - (1 - \sigma_{min})t}\]So far, the conditional probability path and conditional vector field are conditioned on the data \(x_1\) , which is similar to the setup of diffusion modeling. However, the conditioning variable can be general, \(z = (x_1)\) or \(z = (x_1, x_0)\) by coupling the samples of prior and data distribution:
\[q(z) = q(x_0, x_1)\]Example 3: Independent CFM
For independent coupling, \(x_0\) and \(x_1\) are independent:
\[q(z) = q(x_0)q(x_1) = p_0(x_0)p_1(x_1)\]We can use a simple choice of conditional probability path:
\[p_t(x|z) = p_t(x|x_0, x_1) = \mathcal{N}(x| tx_1+(1-t)x_0, \sigma^2)\]For this case
\[\begin{align*} \mu_t(z) = \mu_t(x_0, x_1) = tx_1 + (1-t)x_0 \\ \sigma_t(z) = \sigma_t(x_0, x_1) = \sigma^2 \end{align*}\]Then the conditional vector field is then:
\[u_t(x|z) = u_t(x|x_0, x_1) = x_1 - x_0\]which is the simplest form of flow matching and is quite neat.
The following is the sample code snippet that shapes a Gaussian noisy distribution \(p_0\) into a data distribution \(p_1\), which is a moon distribution.
## Imports
import torch
from torch import nn, Tensor
from sklearn.datasets import make_moons
## Flow class
class Flow(nn.Module):
def __init__(self, dim: int = 2, h: int = 64):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim + 1, h), nn.ELU(),
nn.Linear(h, h), nn.ELU(),
nn.Linear(h, h), nn.ELU(),
nn.Linear(h, dim))
# This is v_{t, \theta}(x) that regress the vector field u_t
def forward(self, t: Tensor, x_t: Tensor) -> Tensor:
return self.net(torch.cat((t, x_t), -1))
# This is for midpoint sampling and we will take a look later
def step(self, x_t: Tensor, t_start: Tensor, t_end: Tensor) -> Tensor:
t_start = t_start.view(1, 1).expand(x_t.shape[0], 1)
return x_t + (t_end - t_start) * self(t=t_start + (t_end - t_start) / 2, x_t= x_t + self(x_t=x_t, t=t_start) * (t_end - t_start) / 2)
## Training
flow = Flow()
optimizer = torch.optim.Adam(flow.parameters(), 1e-2)
loss_fn = nn.MSELoss()
for _ in range(10000):
# Sample t \in [0, 1]
t = torch.rand(len(x_1), 1)
# sample x_1 ~ q
x_1 = Tensor(make_moons(256, noise=0.05)[0])
# sample x_0 ~ p
x_0 = torch.randn_like(x_1)
# compute x_t given sigma_t = 0
x_t = (1 - t) * x_0 + t * x_1
# compute vector field u_t
dx_t = x_1 - x_0
# regress on the vector field
optimizer.zero_grad()
loss_fn(flow(t=t, x_t=x_t), dx_t).backward()
optimizer.step()
What about sampling?
Once we get or approximate the ground truth vector field \(u_t(x_t \mid z)\) we can used it to transform a sampled point anywhere and if we do this iteratively (integrate) from \(t=0\) to \(t=1\), we can recover the data. This can be done using any ODE solver like RK or Euler methods etc.
In the Flow.step function of above code, we used the midpoint method. Say we have an odinary differential equation:
We can use the first order approximation to find \(y(t_0+\Delta t)\):
\[y(t_0+\Delta t) = y(t_0) + \Delta ty'(t_0)\]This can be better approximated using the derivative at the midpoint, namely \(y’(t_0 + \frac{\Delta t}{2})\):
\[y(t_0 + \Delta t) = y(t_0) + \Delta ty'(t_0 + \frac{\Delta t}{2}) = y(t_0) + \Delta tf(t_0 + \frac{\Delta t}{2}, y(t_0+\frac{\Delta t}{2}))\]And the midpoint can be computed
\[y(t_0 + \frac{\Delta t}{2}) = \frac{1}{2}(y(t_0) + y(t_0 + \Delta t))\]But we’re now trying to find \(y(t_0+\Delta t)\). So we need to approximate the midpoint using first order:
\[y(t_0 + \frac{\Delta t}{2}) = y(t_0) + \frac{\Delta t}{2}y'(t_0) = y(t_0) + \frac{\Delta t}{2}f(t_0, y(t_0))\]Finally, we have
\[y(t_0 + \Delta t) = y(t_0) + \Delta tf(t_0 + \frac{\Delta t}{2}, y(t_0) + \frac{\Delta t}{2}f(t_0, y(t_0)))\]So for our samples at \(t\), \(x_t\) given \(u_t(x_t)\)
\[x_{t+dt} = x_t + u_{t+dt/2}\left(x_t + \frac{dt}{2}u_t(x_t)\right)\]For sampling:
x = torch.randn(300, 2)
n_steps = 8
time_steps = torch.linspace(0, 1.0, n_steps + 1)
for i in range(n_steps):
# the distribution path gor pushed forward <-> The data x got transformed by flow
x = flow.step(x_t=x, t_start=time_steps[i], t_end=time_steps[i + 1])
Example 4: Minibatch Optimal Transport CFM
Typically these flow matching (or diffusion) models are trained using minibatch:
- Sample time \(t\in [0, 1]\)
- Sample data \(x_1 \sim p_1 \sim q\) and \(x_0\sim p_0\)
- Compute the noised data \(x_t\) in terms of \(x_0\) and \(x_1\)
- Use the model \(f_{t,\theta}(x_t)\) to regress on the flow vector fields, noises or scores, etc.
The issue for the flow matching model is that these flow vector fields might cross if we sample randomly from \(p_0\) and \(p_1\). This means that at a given noised data \(x_t\) there might exist NON-UNIQUE flow vector field \(u_t(x_t \mid x_0,x_1)\), making the training difficult because the neural net model is one-to-one. It can be mitigated by re-shuffling the minibatch samples via optimal transport.
So at train time we do the following:
- Sample \(t\in[0,1]\)
- Sample data point \(x_1\sim q(x) = p_1(x)\)
- Sample data point \(x_0 \sim p_0(x)\)
- Reshuffle / rearrange minibatch via optimal transport
- Sample \(x_t \sim p_t(x \mid x_0, x_1)\)
- Compute corresponding vector field \(u_t(x_t \mid x_0, x_1)\)
- Use neural network \(v_{t,\theta}(x_t)\) to regress on the vector field \(u_t(x_t \mid x_0, x_1)\)
Example 5: Schrodinger Bridge
The Schrodinger Bridge is trying to vary the conditional variance in the conditional probability path, \(\sigma_t(z) = \sigma_t(x_0, x_1)\) such that \(p_0\) and \(p_1\) respect the prior/data distributions more faithfully.
\[\begin{align*} \mu_t(x_0, x_1) = tx_1 + (1-t)x_0 \\ \sigma_t(x_0, x_1) = \sqrt{t(1-t)}\sigma \end{align*}\]Then the conditional vector field is then:
\[u_t(x|z) = u_t(x|x_0, x_1) = \frac{1-2t}{2t(1-t)}\left[ x-(tx_1 + (1-t)x_0) \right] + (x_1 - x_0)\]It is also possible to train flow and score models at the same time, which is the SF2M model, generating stochastic trajectories in the sampling.
Likelihood calculation?
One benefit of using flow generative model is that they allow the tractable computation of the EXACT likelihood \(\log{p_1(x)}\) for all \(x\). Start from the flow ODE:
\[\frac{d}{dt}\psi_t(x) = u_t(\psi_t(x)); \psi_0(x) = x\]We can use the instantaneous change of variable theorem:
Let \(\mathbf{z}(t)\) be finite continuous random variable with probability \(p(\mathbf{z}(t))\) dependent on time. Let
\[\frac{d\mathbf{z}}{dt} = f(\mathbf{z}(t), t)\]be an ODE that describe a time-dependent transformation. Then the the log likelihood of \(\mathbf{z}\) follows the ODE:
\[\frac{\partial \log{p(\mathbf{z}(t))}}{\partial t} = -\text{tr}\left[\frac{d\mathbf{f}}{d\mathbf{z(t)}} \right] = -(\nabla\cdot\mathbf{f})(\mathbf{z}(t))\]Here \(\mathbf{z} \in \mathbf{R}^d\), \(p: \mathbf{R}^d \to \mathbf{R}\), \(\mathbf{f}: \mathbf{R}^d \times t \to \mathbf{R}^d\).
\[\mathbf{f}(z_1, z_2, ..., z_d, t) = (f_1, f_2, ..., f_d)\] \[\frac{d\mathbf{f}}{d\mathbf{z}} = \begin{bmatrix} \frac{\partial f_1}{\partial z_1} & \frac{\partial f_1}{\partial z_2} & \frac{\partial f_1}{\partial z_3} & \dots & \frac{\partial f_1}{\partial z_d} \\ \frac{\partial f_2}{\partial z_1} & \frac{\partial f_2}{\partial z_2} & \frac{\partial f_2}{\partial z_3} & \dots & \frac{\partial f_2}{\partial z_d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_d}{\partial z_1} & \frac{\partial f_3}{\partial z_2} & \frac{\partial f_d}{\partial z_3} & \dots & \frac{\partial f_d}{\partial z_d} \end{bmatrix}\]Now \(\mathbf{f} \to u_t\) and \(\mathbf{z} \to \psi_t(x)\) we have
\[\frac{\partial \log p_t(\psi_t(x))}{\partial t} = -\text{tr}\left[\frac{\partial u_t}{\partial x}(\psi_t(x)) \right] = -(\nabla\cdot u_t)(\psi_t(x))\]The divergence can be computed using the Hutchinson’s trace estimator
\[\text{tr}(M) = \mathbf{E}_Z\text{tr}[Z^TMZ]\]where \(\mathbf{E}[Z]=0\) and \(\text{Cov}(Z, Z) = I\) for a fixed sample of \(Z\).
Let’s call \(\psi_t(x) = f(t)\) and \(\log{p_t(\psi_t(x))} = g(t)\) and we have access to \(u_t\). Computing an unbiased estimate of \(\log{p_1(x)}\) involves simulating the following set of ODEs back in time:
\[\begin{align} \frac{df}{dt} = u_t(f(t)) \\ \frac{dg}{dt} = -\text{tr}\left[Z^T\frac{\partial u_t}{\partial x}(f(t)) Z \right] \end{align}\]with \(f(1) = x\) and \(g(1) = 0\)
\[\log{p_1(x)} = \log{p_0(f(0))} - g(0)\]def compute_likelihood(
self,
x_1: Tensor,
log_p0: Callable[[Tensor], Tensor],
step_size: Optional[float],
method: str = "euler",
atol: float = 1e-5,
rtol: float = 1e-5,
time_grid: Tensor = torch.tensor([1.0, 0.0]),
return_intermediates: bool = False,
exact_divergence: bool = False,
enable_grad: bool = False,
**model_extras,
) -> Union[Tuple[Tensor, Tensor], Tuple[Sequence[Tensor], Tensor]]:
r"""Solve for log likelihood given a target sample at :math:`t=0`.
Works similarly to sample, but solves the ODE in reverse to compute the log-likelihood. The velocity model must be differentiable with respect to x.
The function assumes log_p0 is the log probability of the source distribution at :math:`t=0`.
Args:
x_1 (Tensor): target sample (e.g., samples :math:`X_1 \sim p_1`).
log_p0 (Callable[[Tensor], Tensor]): Log probability function of the source distribution.
step_size (Optional[float]): The step size. Must be None for adaptive step solvers.
method (str): A method supported by torchdiffeq. Defaults to "euler". Other commonly used solvers are "dopri5", "midpoint" and "heun3". For a complete list, see torchdiffeq.
atol (float): Absolute tolerance, used for adaptive step solvers.
rtol (float): Relative tolerance, used for adaptive step solvers.
time_grid (Tensor): If step_size is None then time discretization is set by the time grid. Must start at 1.0 and end at 0.0, otherwise the likelihood computation is not valid. Defaults to torch.tensor([1.0, 0.0]).
return_intermediates (bool, optional): If True then return intermediate time steps according to time_grid. Otherwise only return the final sample. Defaults to False.
exact_divergence (bool): Whether to compute the exact divergence or use the Hutchinson estimator.
enable_grad (bool, optional): Whether to compute gradients during sampling. Defaults to False.
**model_extras: Additional input for the model.
Returns:
Union[Tuple[Tensor, Tensor], Tuple[Sequence[Tensor], Tensor]]: Samples at time_grid and log likelihood values of given x_1.
"""
assert (
time_grid[0] == 1.0 and time_grid[-1] == 0.0
), f"Time grid must start at 1.0 and end at 0.0. Got {time_grid}"
# Fix the random projection for the Hutchinson divergence estimator
if not exact_divergence:
z = (torch.randn_like(x_1).to(x_1.device) < 0) * 2.0 - 1.0
def ode_func(x, t):
return self.velocity_model(x=x, t=t, **model_extras)
def dynamics_func(t, states):
xt = states[0]
with torch.set_grad_enabled(True):
xt.requires_grad_()
ut = ode_func(xt, t)
if exact_divergence:
# Compute exact divergence
div = 0
for i in range(ut.flatten(1).shape[1]):
div += gradient(ut[:, i], xt, create_graph=True)[:, i]
else:
# Compute Hutchinson divergence estimator E[z^T D_x(ut) z]
ut_dot_z = torch.einsum(
"ij,ij->i", ut.flatten(start_dim=1), z.flatten(start_dim=1)
)
grad_ut_dot_z = gradient(ut_dot_z, xt)
div = torch.einsum(
"ij,ij->i",
grad_ut_dot_z.flatten(start_dim=1),
z.flatten(start_dim=1),
)
return ut.detach(), div.detach()
y_init = (x_1, torch.zeros(x_1.shape[0], device=x_1.device))
ode_opts = {"step_size": step_size} if step_size is not None else {}
with torch.set_grad_enabled(enable_grad):
sol, log_det = odeint(
dynamics_func,
y_init,
time_grid,
method=method,
options=ode_opts,
atol=atol,
rtol=rtol,
)
x_source = sol[-1]
source_log_p = log_p0(x_source)
if return_intermediates:
return sol, source_log_p + log_det[-1]
else:
return sol[-1], source_log_p + log_det[-1]
Implementation of 2D Case
Here, we are going to implement the I-CFM, OT-CFM, Schrodinger Bridge CFM and SF2M for the following generative examples:
- Generating moon from 8 Gaussians
- Generating moon from noises
- Generating checkerboard from noises
- Generating 8 gaussains from noises And compute the corresponding likelihoods.
Some library imports:
import os, math, torch, time, copy
import ot as pot
import numpy as np
import matplotlib.pyplot as plt
assert torch.cuda.is_available()
print(torch.cuda.device_count())
DEVICE = torch.device('cuda')
from tqdm import tqdm
from functools import partial
# torchdyn libraries
from torchdyn.core import NeuralODE
from torchdyn.datasets import generate_moons
# for likelihood computation
import torchdiffeq
from typing import Optional
from torch import Tensor
from torch.distributions import Independent, Normal
Some utils functions and distributions
# Important utils functions
def sample_conditional_pt(x0, x1, t, sigma):
'''
Draw a sample from N(mu_t(x0, x1), sigma), where
mu_t(x0, x1) = t * x1 + (1 - t) * x0 being the interpolation between x0 and x1
'''
assert x0.shape == x1.shape
assert t.shape[0] == x0.shape[0]
t = t[..., None]
mu_t = t * x1 + (1. - t) * x0
epsilon = torch.randn_like(x0)
return mu_t + sigma * epsilon
# conditional vector field
def conditional_vector_field(x0, x1, t, xt):
'''
Compute the conditional vector fields u_t(x| x0, x1) = sigma_t' (x - mu_t) / sigma_t + mu_t'
Since sigma_t = sigma is a constant, sigma_t' = 0 in the above scenerio
u_t(x| x0, x1) = mu_t' = x1 - x0
'''
return x1 - x0
# functions for the data utils
# sample 8 gaussians
def eight_normal_sample(n, dim, scale=1, var=1):
m = torch.distributions.multivariate_normal.MultivariateNormal(torch.zeros(dim), math.sqrt(var) * torch.eye(dim))
centers = [(1, 0),
(-1, 0),
(0, 1),
(0, -1),
(1.0 / np.sqrt(2), 1.0 / np.sqrt(2)),
(1.0 / np.sqrt(2), -1.0 / np.sqrt(2)),
(-1.0 / np.sqrt(2), 1.0 / np.sqrt(2)),
(-1.0 / np.sqrt(2), -1.0 / np.sqrt(2))]
centers = torch.tensor(centers) * scale
noise = m.sample((n,))
multi = torch.multinomial(torch.ones(8), n, replacement=True)
data = []
for i in range(n): data.append(centers[multi[i]] + noise[i])
data = torch.stack(data)
return data
def sample_8_gaussians(batch_size):
return eight_normal_sample(batch_size, 2, scale=5, var=0.1).float()
# sample moons
def sample_moons(batch_size):
x0, _ = generate_moons(batch_size, noise=0.2)
return x0 * 3 - 1
# sample Gaussians
def sample_noise(batch_size, dim=2):
return torch.randn(batch_size, dim)
def sample_checkerboard_data(n_points, n_squares=4, noise=0.01, scale=5):
# Create a grid
x = np.linspace(0, 1, n_squares + 1)
y = np.linspace(0, 1, n_squares + 1)
xx, yy = np.meshgrid(x[:-1], y[:-1])
# Create the checkerboard pattern
pattern = np.zeros((n_squares, n_squares))
pattern[::2, ::2] = 1
pattern[1::2, 1::2] = 1
# Generate points
points = []
for i in range(n_squares):
for j in range(n_squares):
if pattern[i, j] == 1:
n = n_points // (n_squares * n_squares // 2)
x = np.random.uniform(xx[i,j], xx[i,j] + 1/n_squares, n)
y = np.random.uniform(yy[i,j], yy[i,j] + 1/n_squares, n)
points.extend(list(zip(x, y)))
# Convert to numpy array and add noise
points = np.array(points)
points += np.random.normal(0, noise, points.shape) - np.ones(2) * 0.5
points = torch.from_numpy(points).to(torch.float)
return points * scale
# plot the trajs
def plot_trajs(trajs, n_steps, flow_line=True):
n_traj = len(trajs)
fig, ax = plt.subplots(1, n_traj, figsize=(25, 5), dpi=150)
for i, traj in enumerate(trajs):
if flow_line:
ax[i].scatter(traj[:, :, 0], traj[:, :, 1], s=0.2, alpha=0.2, c='olive')
ax[i].scatter(traj[0, :, 0], traj[0, :, 1], s=10, alpha=0.8, c='black')
ax[i].scatter(traj[-1, :, 0], traj[-1, :, 1], s=4, alpha=1, c='tab:red')
legend = ['Flow'] if flow_line else []
legend += ['Prior sample ~ p0', 'Data sample ~ p1']
ax[i].legend(legend)
ax[i].set_xticks([])
ax[i].set_yticks([])
ax[i].set_title(f'checkpoint at step {(i + 1) * (n_steps // n_traj)}')
plt.show()
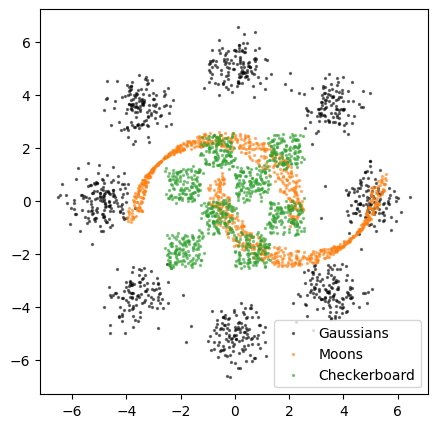
Let’s take a look at what kind of data we are dealing with:
batch_size = 1000
g8, mn, cb = sample_8_gaussians(batch_size), sample_moons(batch_size), sample_checkerboard_data(batch_size)
fig, ax = plt.subplots(1, figsize=(5, 5))
ax.scatter(g8[:, 0], g8[:, 1], alpha=0.5, color='black', s=2, label='Gaussians')
ax.scatter(mn[:, 0], mn[:, 1], alpha=0.5, color='tab:orange', s=2, label='Moons')
ax.scatter(cb[:, 0], cb[:, 1], alpha=0.5, color='tab:green', s=2, label='Checkerboard')
plt.legend()
plt.show()
Ok, now to the model, which is just a shallow MLP, taking \((x, t)\) and outputting the conditional vector fields.
class MLP(torch.nn.Module):
def __init__(self, dim, out_dim=None, hidden_dim=128, time_varying=False):
super(MLP, self).__init__()
self.time_varying = time_varying
if out_dim is None: out_dim = dim
self.net = torch.nn.Sequential(torch.nn.Linear(dim + int(time_varying), hidden_dim),
torch.nn.SELU(),
torch.nn.Linear(hidden_dim, hidden_dim),
torch.nn.SELU(),
torch.nn.Linear(hidden_dim, hidden_dim),
torch.nn.SELU(),
torch.nn.Linear(hidden_dim, out_dim))
def forward(self, x): return self.net(x)
class torch_wrapper(torch.nn.Module):
'''Wraps model to torchdyn compatible format.'''
def __init__(self, model):
super(torch_wrapper, self).__init__()
self.model = model
def forward(self, t, x, *args, **kwargs):
return self.model(torch.cat([x, t.repeat(x.shape[0])[..., None]], 1))
The first 3 cases can be wrapped in a function, since they only differ in the design of \(p_t\) and \(u_t\).
# sampling wrapper
def sampling(prior_samples, checkpoints):
trajs = []
for checkpoint in tqdm(checkpoints, desc='sampling from checkpoint'):
node = NeuralODE(torch_wrapper(checkpoint), solver="dopri5", sensitivity="adjoint", atol=1e-4, rtol=1e-4)
with torch.no_grad():
traj = node.trajectory(prior_samples, t_span=torch.linspace(0, 1, 100)) # integrating from 0 to 1 in 100 steps
trajs.append(traj.cpu().numpy())
return trajs
# cfm training wrapper:
def cfm_wrapper(p0_sampler, p1_sampler, pt_sampler, vector_field, ot_sampler=None, batch_size=2048, n_steps=20000, likelihood=False):
sigma = 0.01
dim = 2
n_checkpoints = 5
model = MLP(dim=dim, time_varying=True).to(DEVICE)
optimizer = torch.optim.AdamW(model.parameters())
checkpoints = []
pbar = tqdm(range(n_steps + 1))
for k in pbar:
# sample x0 ~ p0 and x1 ~ p1
x0 = p0_sampler(batch_size).to(DEVICE)
x1 = p1_sampler(batch_size).to(DEVICE)
# minibatch Optimal Transport
# match rows using OT plan
if ot_sampler is not None:
x0, x1 = ot_sampler.sample_plan(x0, x1)
# sample time
t = torch.rand(x0.shape[0], dtype=x0.dtype, device=DEVICE)
# sample xt ~ pt conditional probability path
xt = pt_sampler(x0, x1, t, sigma=sigma)
# compute the conditional vector field
ut = vector_field(x0, x1, t, xt)
# the model input is the noisy point xt and time
# the model output is the flow to matching that of ut
vt = model(torch.cat([xt, t[..., None]], dim=-1))
# loss is the conditional flow matching loss, L_CFM
loss = ((vt - ut) ** 2).mean()
optimizer.zero_grad()
loss.backward()
optimizer.step()
if k % 100 == 0: pbar.set_description(f'Training step {k:06d}, loss = {loss.item():.3f}')
if (k > 0) and (k % (n_steps // n_checkpoints) == 0): checkpoints.append(copy.deepcopy(model))
# sampling
# Generating samples x0' ~ p0
prior_samples = p0_sampler(batch_size).to(DEVICE)
# use the model to get estimate of ut and use it to transform the x0' iteratively (integrate)
trajs = sampling(prior_samples, checkpoints)
# plotting
plot_trajs(trajs, n_steps=n_steps, flow_line=True)
# compute likelihood
if likelihood:
x_1, lls = compute_likelihood_checkpoints(checkpoints, exact_divergence=False)
plot_likelihood(x_1, lls, n_steps)
return None
Here we will define the compute_likelihood_checkpoints and plot_likelihood functions:
# compute the gradient for the divergence calculation
def gradient(output: Tensor, x: Tensor, grad_outputs: Optional[Tensor] = None, create_graph: bool = False) -> Tensor:
"""
Compute the gradient of the inner product of output and grad_outputs w.r.t :math:`x`.
Args:
output (Tensor): [N, D] Output of the function.
x (Tensor): [N, d_1, d_2, ... ] input
grad_outputs (Optional[Tensor]): [N, D] Gradient of outputs, if `None`,
then will use a tensor of ones
create_graph (bool): If True, graph of the derivative will be constructed, allowing
to compute higher order derivative products. Defaults to False.
Returns:
Tensor: [N, d_1, d_2, ... ]. the gradient w.r.t x.
"""
if grad_outputs is None: grad_outputs = torch.ones_like(output).detach()
grad = torch.autograd.grad(output, x, grad_outputs=grad_outputs, create_graph=create_graph)[0]
return grad
def compute_likelihood(x_1, model, log_p0, exact_divergence=False, n_evals=25, solver_method='dopri5', solver_opts={}):
assert x_1.device == next(model.parameters()).device
device = x_1.device
# fixed time range from 1.0 to 0.0
time_range = torch.tensor([1.0, 0.0], device=device)
# random projection vectors for the Hutchinson divergence, constant w.r.t x
# we should use the same z at any given time point, faster doing so as well
z = (torch.randn_like(x_1) < 0) * 2.0 - 1.0 if not exact_divergence else None
# === ODE System ===
# set up the ODE equations for the likelihood calculation
def ode_system(t, states):
'''
states = (x_t, log p_t(x_t))
'''
x_t = states[0]
with torch.set_grad_enabled(True):
x_t.requires_grad_()
u_t = model(t, x_t)
# compute the exact divergence one by one
if exact_divergence:
assert z is None
div = 0
for i in range(u_t.flatten(1).shape[1]):
# definition of divergence of a neural network
# using autograd through NN and sum over du_i/dx_i
div += gradient(u_t[:, i], x_t, create_graph=True)[:, i]
# compute the divergence estimator using Hutchinson's formula
else:
assert z is not None
# ut * z
ut_dot_z = torch.einsum('ij,ij->i', u_t.flatten(start_dim=1), z.flatten(start_dim=1))
# [d (ut)/ dx] * z = d (ut * z) / dx
grad_ut_dot_z = gradient(ut_dot_z, x_t)
# z^T * [d (ut)/ dx] * z = z^T * d (ut * z) / dx
div = torch.einsum('ij,ij->i', grad_ut_dot_z.flatten(start_dim=1), z.flatten(start_dim=1))
# just keep the values not the computational graph
return u_t.detach(), div.detach()
# === End of ODE System ===
# init state
state_init = (x_1, torch.zeros(x_1.shape[0], device=device))
# doing the integration back in time from 1.0 to 0.0
likelihoods = []
for _ in range(n_evals):
# do reverse in time
with torch.set_grad_enabled(False):
sol, log_det = torchdiffeq.odeint(ode_system, state_init, time_range,
method=solver_method,
options=solver_opts,
atol=1e-5,
rtol=1e-5)
# x_0 and g_0
x_0, g_0 = sol[-1], log_det[-1]
log_p0_x0 = log_p0(x_0)
log_p1_x1 = log_p0_x0 + g_0
likelihood = torch.exp(log_p1_x1).detach().cpu().numpy()
likelihoods.append(likelihood)
return np.stack(likelihoods).mean(0)
# compute likelihood for all checkpoints:
def compute_likelihood_checkpoints(checkpoints, xy=5, grid_size=200, exact_divergence=False, n_evals=25, solver_method='dopri5', solver_opts={}):
# compute likelihood for the grid x_1
x_1 = torch.meshgrid(torch.linspace(-xy, xy, grid_size), torch.linspace(-xy, xy, grid_size))
x_1 = torch.stack([x_1[0].flatten(), x_1[1].flatten()], dim=1).to(DEVICE)
# log_p0
log_p0 = Independent(Normal(torch.zeros(2, device=DEVICE), torch.ones(2, device=DEVICE)), 1).log_prob
# likelihoods
likelihoods = [compute_likelihood(x_1, torch_wrapper(checkpoint), log_p0, exact_divergence=exact_divergence, n_evals=n_evals, solver_method=solver_method, solver_opts=solver_opts) for checkpoint in tqdm(checkpoints, desc='Computing Likelihood')]
return x_1.detach().cpu().numpy(), likelihoods
# plot the likelihoods
def plot_likelihood(x_1, likelihoods, n_steps):
n_likelihoods = len(likelihoods)
fig, ax = plt.subplots(1, n_likelihoods, figsize=(25, 5), dpi=150)
for i, ll in enumerate(likelihoods):
vmin, vmax = 0.0, ll.max() * 0.8
ax[i].scatter(x_1[:, 0], x_1[:, 1], c=ll, cmap='coolwarm', vmin=vmin, vmax=vmax)
ax[i].set_xticks([])
ax[i].set_yticks([])
ax[i].set_title(f'checkpoint at step {(i + 1) * (n_steps // n_likelihoods)}')
plt.show()
1. I-CFM
1-1. 8-Gaussian to Moon:
cfm_wrapper(sample_8_gaussians, sample_moons, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=None)
# loss ~ 7.572
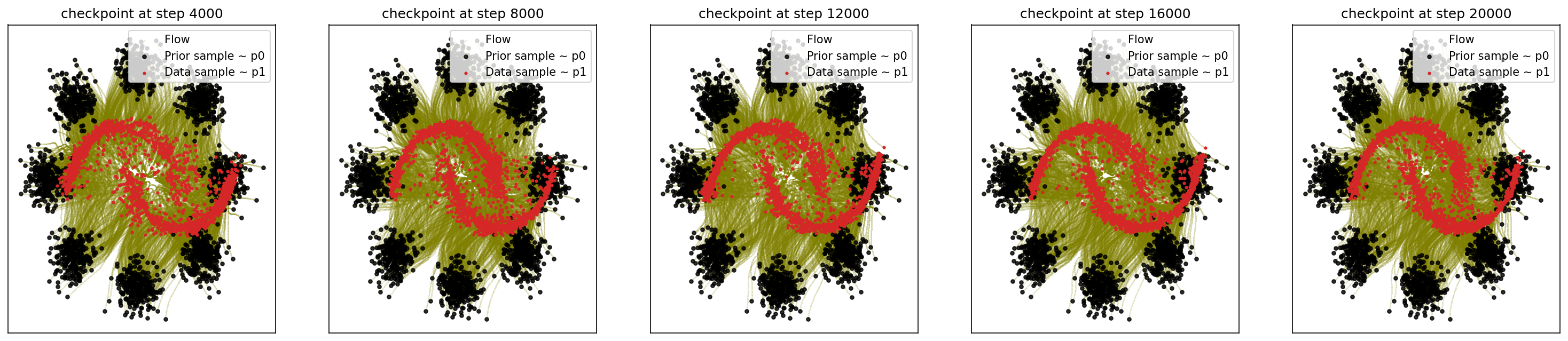
1-2. Generating Moon
cfm_wrapper(sample_noise, sample_moons, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=None, likelihood=True)
# loss ~ 2.839
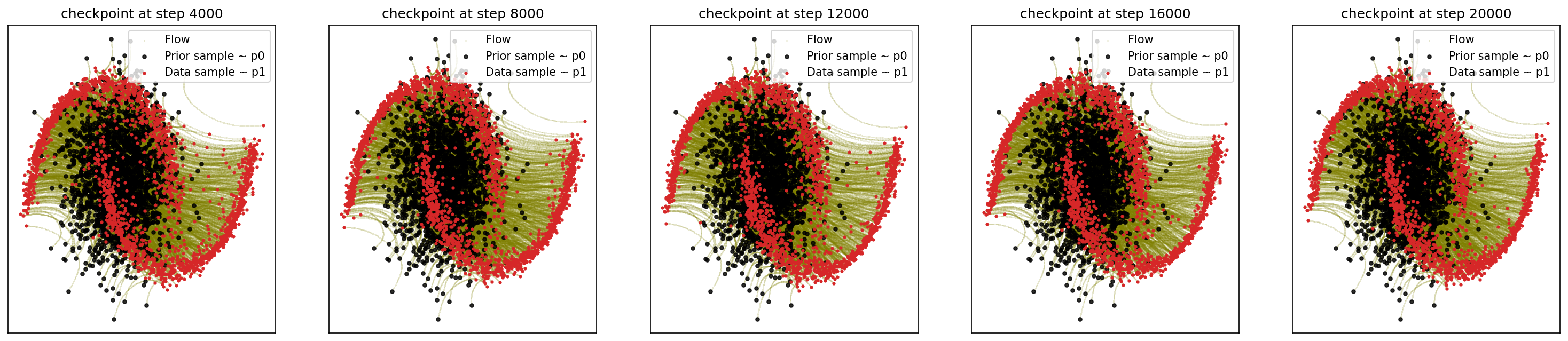
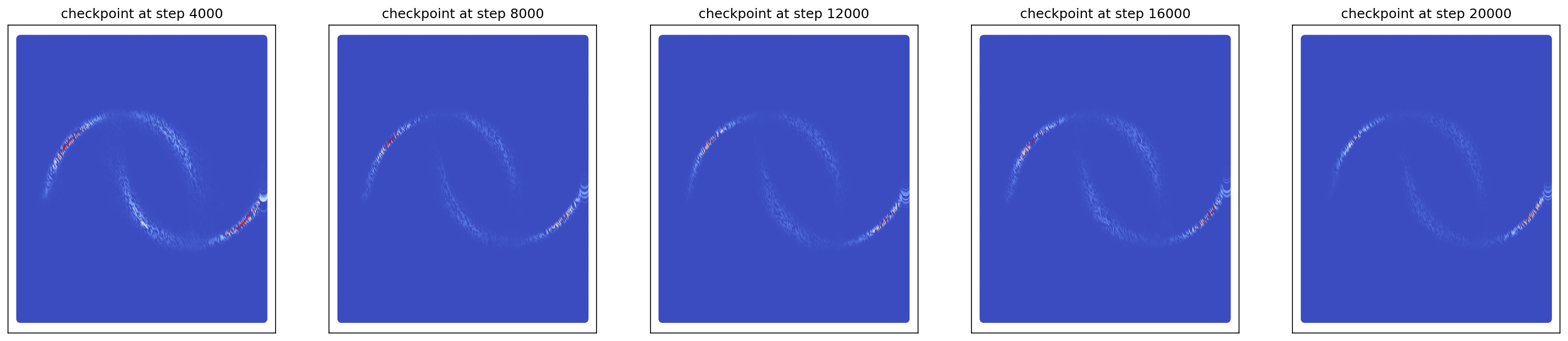
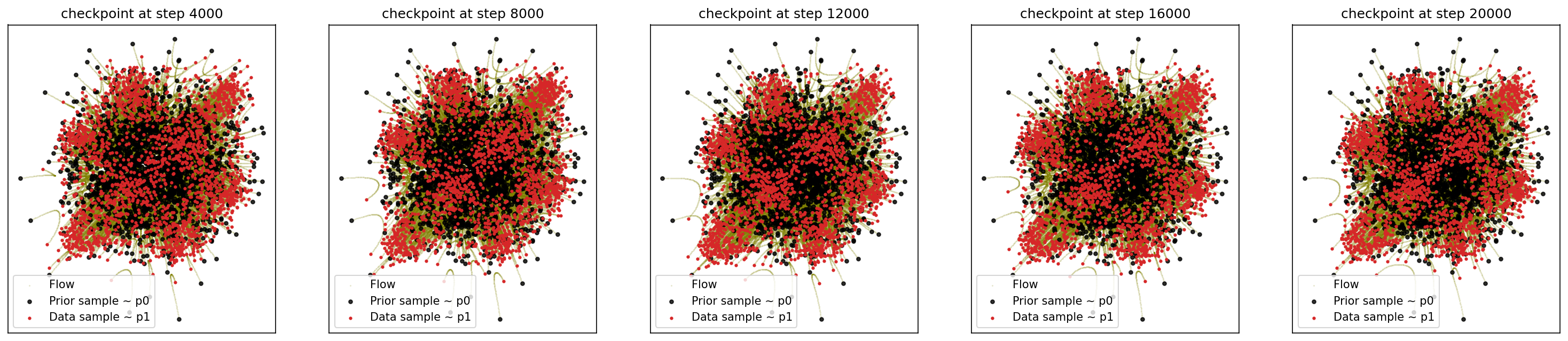
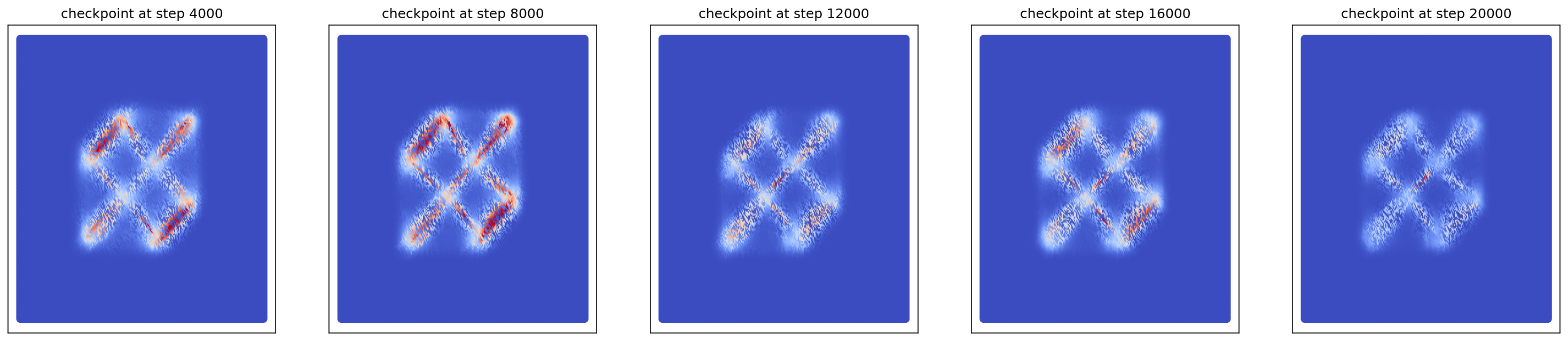
1-3. Generating Checkerboard
cfm_wrapper(sample_noise, sample_checkerboard_data, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=None, likelihood=True)
# loss ~ 2.113
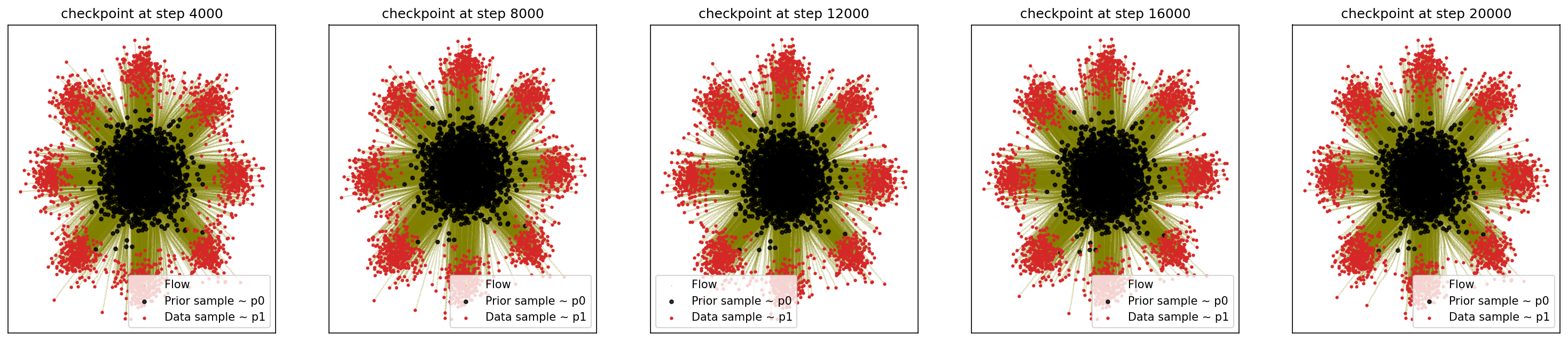
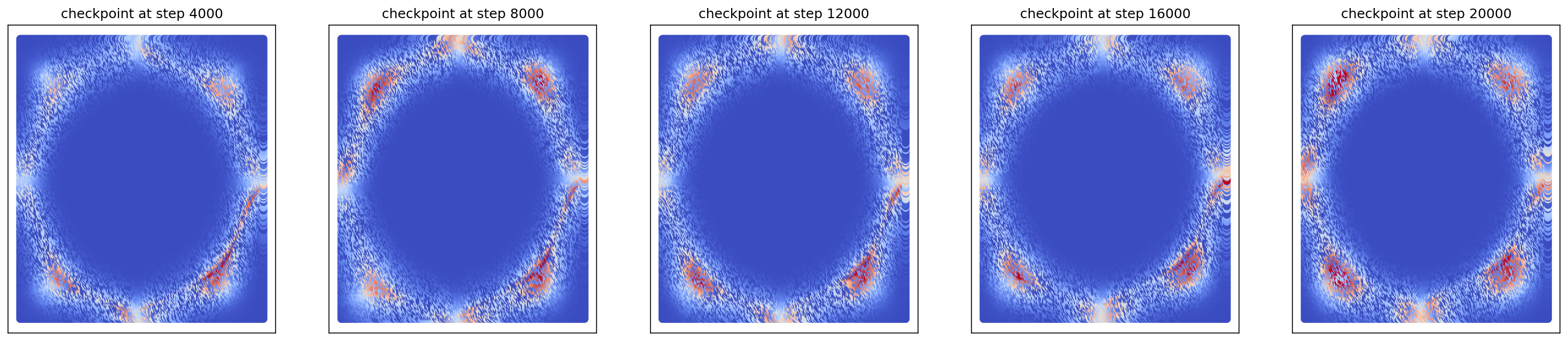
1-4. Generating 8-Gaussians
cfm_wrapper(sample_noise, sample_8_gaussians, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=None, likelihood=True)
# loss ~ 4.999
2. Minibatch OT-CFM
For Minibatch OT, we aim to straighten or tidy up the flow line so that they don’t cross for that specific minibatch to make the learning easily
class OTPlanSampler:
def __init__(self, method='exact', normalize_cost=False, num_threads=1):
if method == 'exact': self.ot_fn = partial(pot.emd, numThreads=num_threads)
elif method == 'sinkhorn': self.ot_fn = partial(pot.sinkhorn, reg=0.05)
else: raise NotImplementedError()
self.normalize_cost = normalize_cost
def get_map(self, x0, x1):
a, b = pot.unif(x0.shape[0]), pot.unif(x1.shape[0])
if x0.dim() > 2: x0 = x0.reshape(x0.shape[0], -1)
if x1.dim() > 2: x1 = x1.reshape(x1.shape[0], -1)
x1 = x1.reshape(x1.shape[0], -1)
M = torch.cdist(x0, x1) ** 2
if self.normalize_cost: M = M / M.max() # should not be normalized when using minibatches
p = self.ot_fn(a, b, M.detach().cpu().numpy())
if not np.all(np.isfinite(p)):
print("ERROR: p is not finite")
print(p)
print("Cost mean, max", M.mean(), M.max())
print(x0, x1)
if np.abs(p.sum()) < 1e-8: p = np.ones_like(p) / p.size
return p
def sample_map(self, pi, batch_size, replace=True):
p = pi.flatten()
p = p / p.sum()
choices = np.random.choice(pi.shape[0] * pi.shape[1], p=p, size=batch_size, replace=replace)
return np.divmod(choices, pi.shape[1])
def sample_plan(self, x0, x1, replace=True):
pi = self.get_map(x0, x1)
i, j = self.sample_map(pi, x0.shape[0], replace=replace)
return x0[i], x1[j]
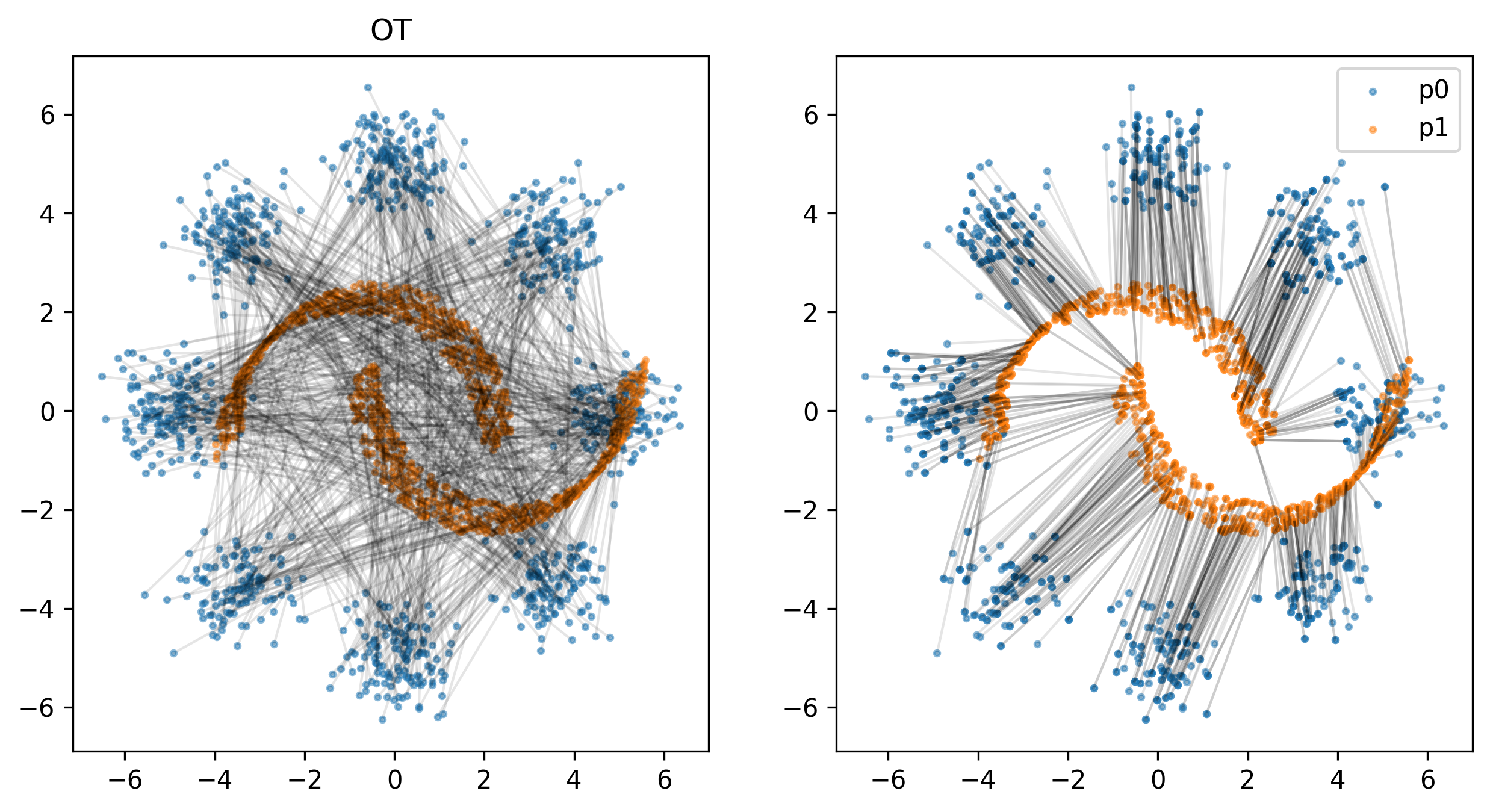
Let’s see what OT did for the data:
# generate samples from p0 and p1
tmp0, tmp1 = sample_8_gaussians(batch_size), sample_moons(batch_size)
# the data p0 and p1 is generated randomly, so in minibatch, we try to match first row of p0 to first row of p1
# this results in crossing of the flow paths or the vector fields
ot_sampler = OTPlanSampler()
tmp0ot, tmp1ot = ot_sampler.sample_plan(tmp0, tmp1)
fig, axes = plt.subplots(1, 2, figsize=(10, 5), dpi=300)
axes[0].scatter(tmp0[:, 0], tmp0[:, 1], s=5, alpha=0.5, label='p0')
axes[0].scatter(tmp1[:, 0], tmp1[:, 1], s=5, alpha=0.5, label='p1')
for i in range(batch_size): axes[0].plot([tmp0[i, 0], tmp1[i, 0]], [tmp0[i, 1], tmp1[i, 1]], color='black', alpha=0.1, lw=1)
axes[0].set_title('Original')
axes[1].scatter(tmp0ot[:, 0], tmp0ot[:, 1], s=5, alpha=0.5, label='p0')
axes[1].scatter(tmp1ot[:, 0], tmp1ot[:, 1], s=5, alpha=0.5, label='p1')
for i in range(batch_size): axes[1].plot([tmp0ot[i, 0], tmp1ot[i, 0]], [tmp0ot[i, 1], tmp1ot[i, 1]], color='black', alpha=0.1, lw=1)
axes[0].set_title('OT')
plt.legend()
plt.show()
2-1. 8-Gaussian to Moon:
cfm_wrapper(sample_8_gaussians, sample_moons, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=OTPlanSampler(), n_steps=10000)
# loss ~ 0.053

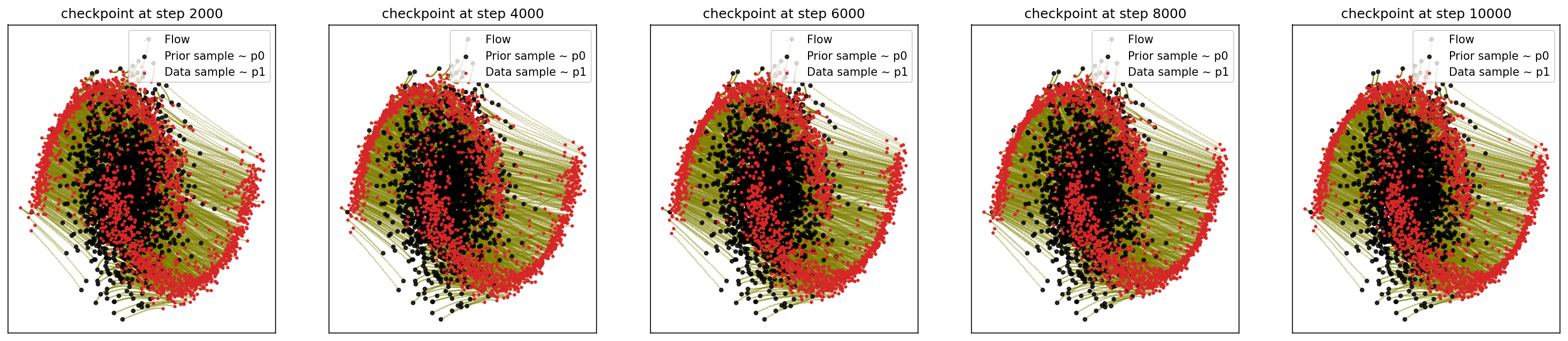
2-2. Generating Moon
cfm_wrapper(sample_noise, sample_moons, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=OTPlanSampler(), n_steps=10000, likelihood=True)
# loss ~ 0.014
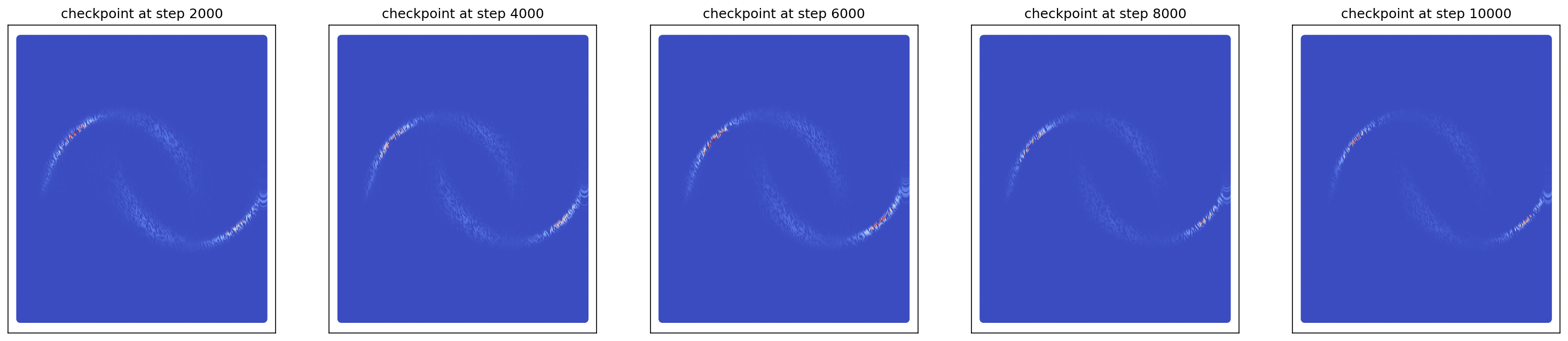
2-3. Generating Checkerboard
cfm_wrapper(sample_noise, sample_checkerboard_data, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=OTPlanSampler(), n_steps=10000, likelihood=True)
# loss ~ 0.013
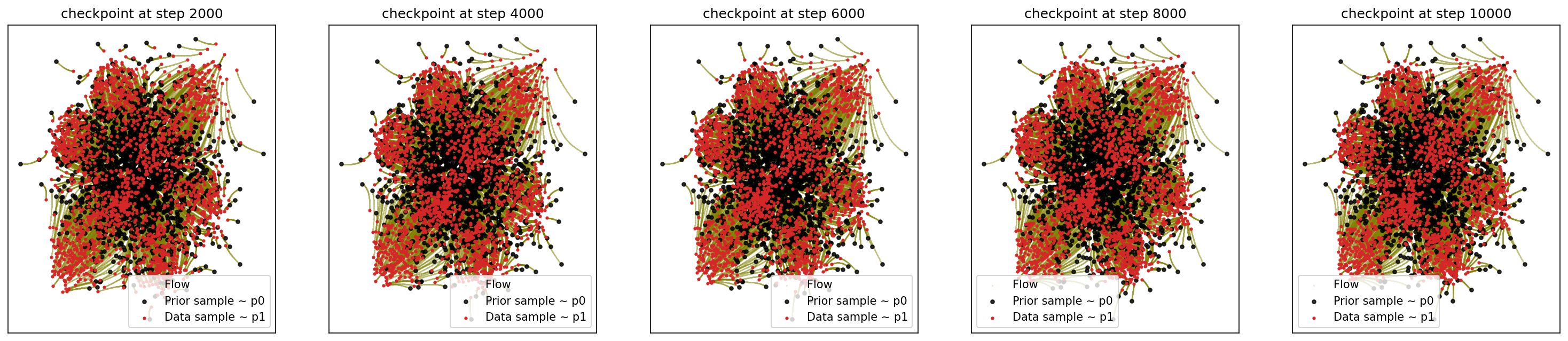
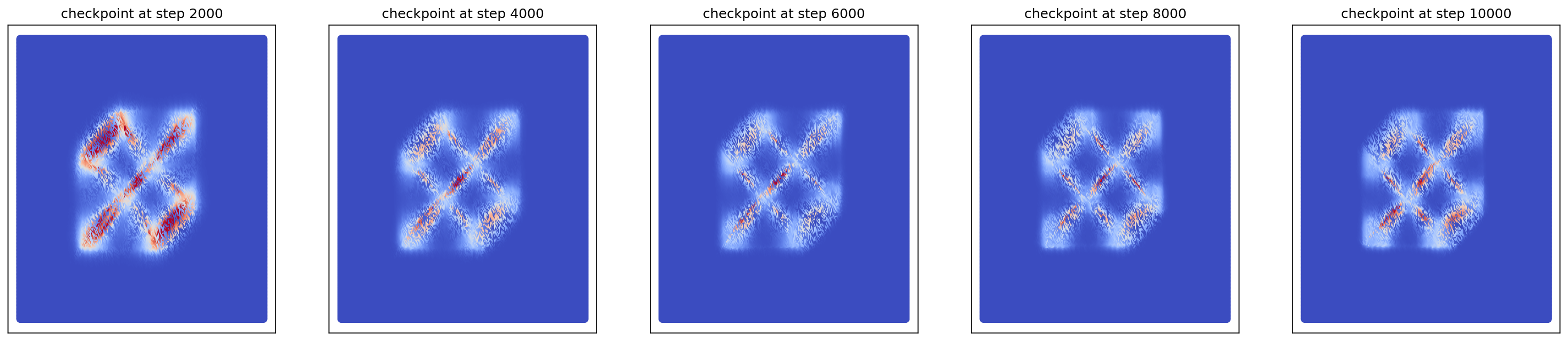
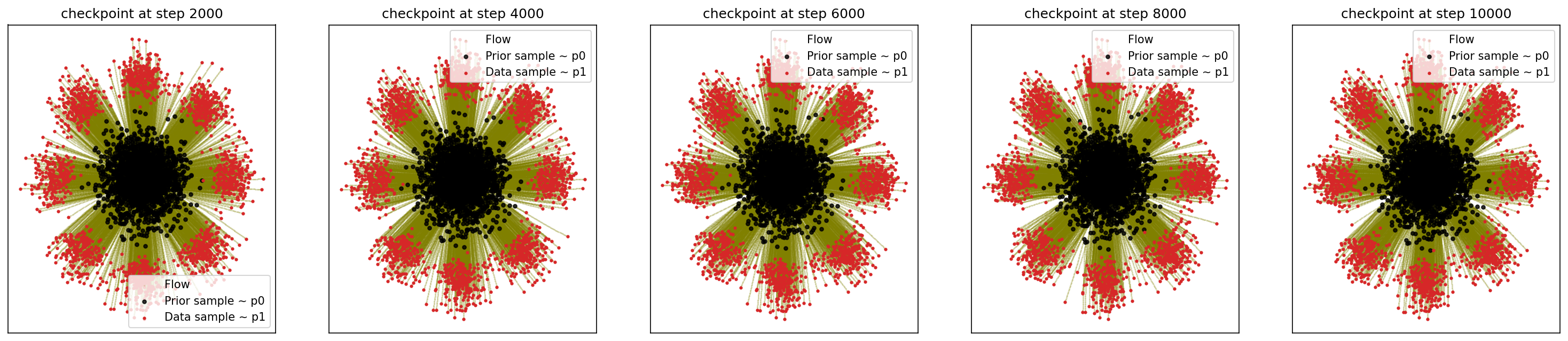
2-4. Generating 8-Gaussians
cfm_wrapper(sample_noise, sample_8_gaussians, pt_sampler=sample_conditional_pt, vector_field=conditional_vector_field, ot_sampler=OTPlanSampler(), n_steps=10000, likelihood=True)
# loss ~ 0.020

3. Schrodinger Bridge
# Let's try using Schrodinger Bridge
# for SB, We keep the mu as previous but change variance to be time-dependent: var = t(1-t)sigma^2
# this changes the flow vector field so we need to rewrite "sample_conditional_pt" and "conditional_vector_field" functions
def sample_conditional_pt_SB(x0, x1, t, sigma=1.0):
'''
Draw a sample from N(mu_t(x0, x1), sigma), where
mu_t(x0, x1) = t * x1 + (1 - t) * x0 being the interpolation between x0 and x1
sigma_t^2 = t * (1-t) * sigma^2
'''
assert x0.shape == x1.shape
assert t.shape[0] == x0.shape[0]
t = t[..., None]
mu_t = t * x1 + (1. - t) * x0
sigma_t = sigma * torch.sqrt(t * (1. - t))
epsilon = torch.randn_like(x0)
return mu_t + sigma_t * epsilon
def conditional_vector_field_SB(x0, x1, t, xt):
'''
Compute the conditional vector fields u_t(x| x0, x1) = sigma_t' (x - mu_t) / sigma_t + mu_t'
Since sigma_t = sigma is a constant, sigma_t' = 0 in the above scenerio
u_t(x| x0, x1) = mu_t' = x1 - x0
'''
assert x0.shape == x1.shape == xt.shape
assert t.shape[0] == x0.shape[0]
t = t[..., None]
mu_t = t * x1 + (1. - t) * x0
sigma_t_prime_over_sigma_t = (1 - 2 * t) / (2 * t * (1 - t) + 1e-8)
ut = sigma_t_prime_over_sigma_t * (xt - mu_t) + x1 - x0
return ut
3-1. 8-Gaussian to Moon:
cfm_wrapper(sample_8_gaussians, sample_moons, pt_sampler=sample_conditional_pt_SB, vector_field=conditional_vector_field_SB, ot_sampler=OTPlanSampler(), n_steps=10000)
# loss ~ 0.044
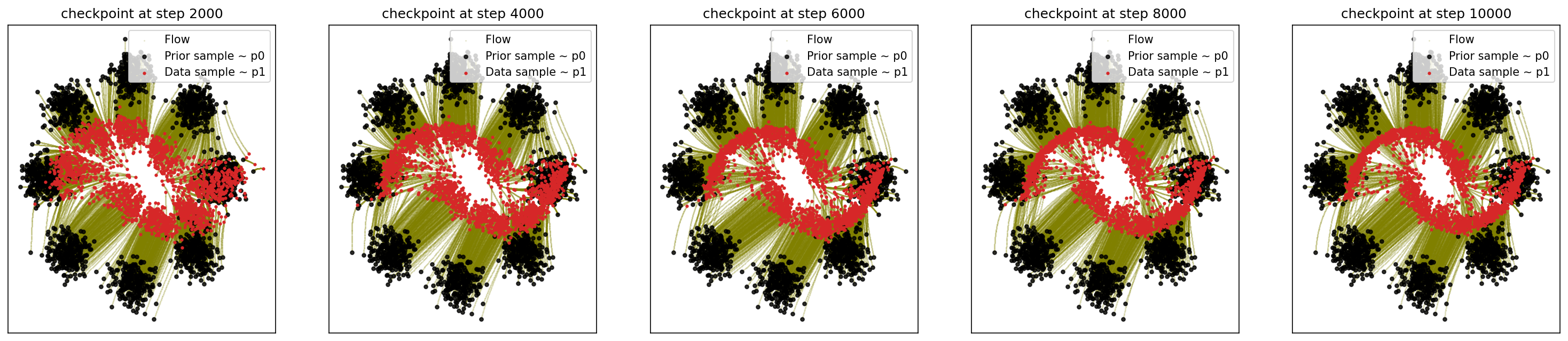
3-2. Generating Moon:
cfm_wrapper(sample_noise, sample_moons, pt_sampler=sample_conditional_pt_SB, vector_field=conditional_vector_field_SB, ot_sampler=OTPlanSampler(), n_steps=10000, likelihood=True)
# loss ~ 0.012
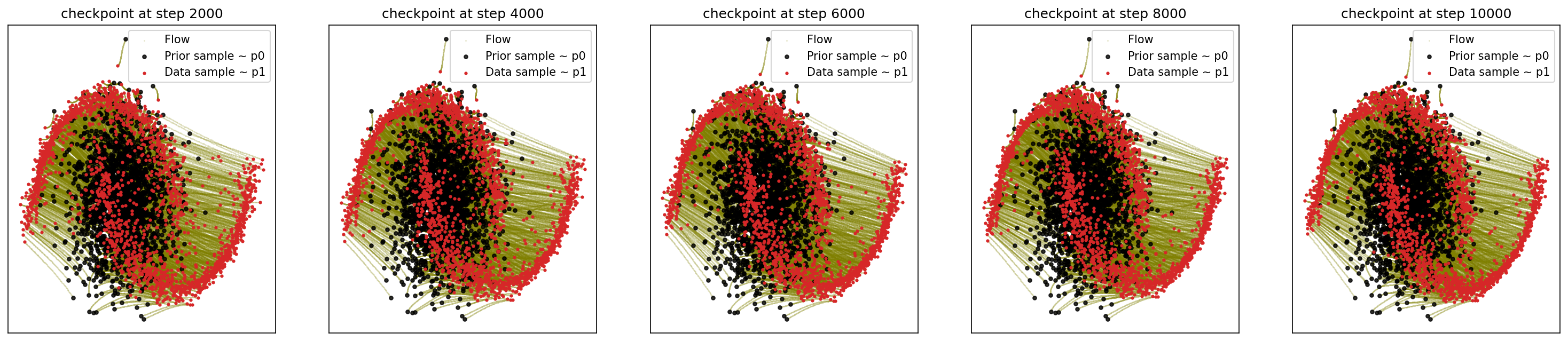
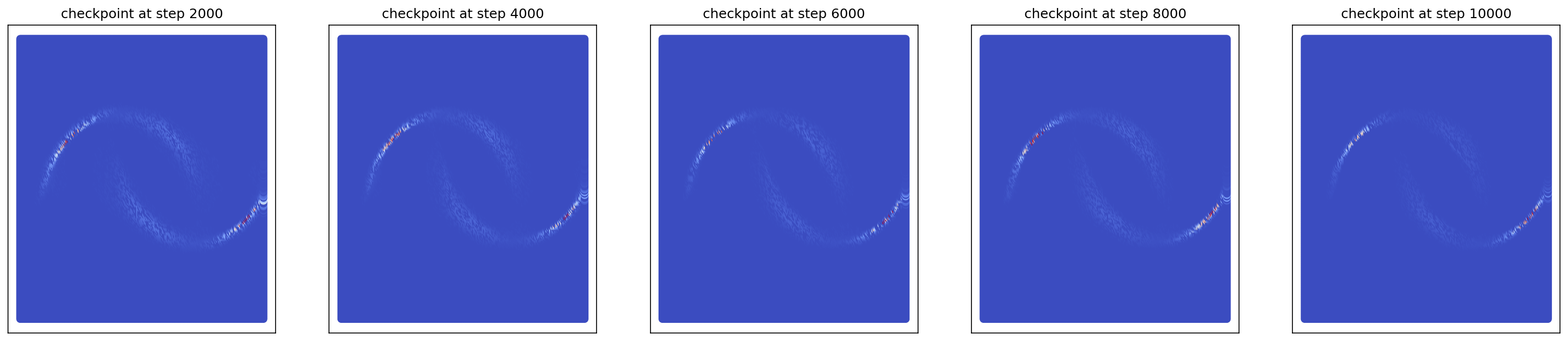
3-3. Generating Checkerboard
cfm_wrapper(sample_noise, sample_checkerboard_data, pt_sampler=sample_conditional_pt_SB, vector_field=conditional_vector_field_SB, ot_sampler=OTPlanSampler(), n_steps=10000, likelihood=True)
# loss ~ 0.011
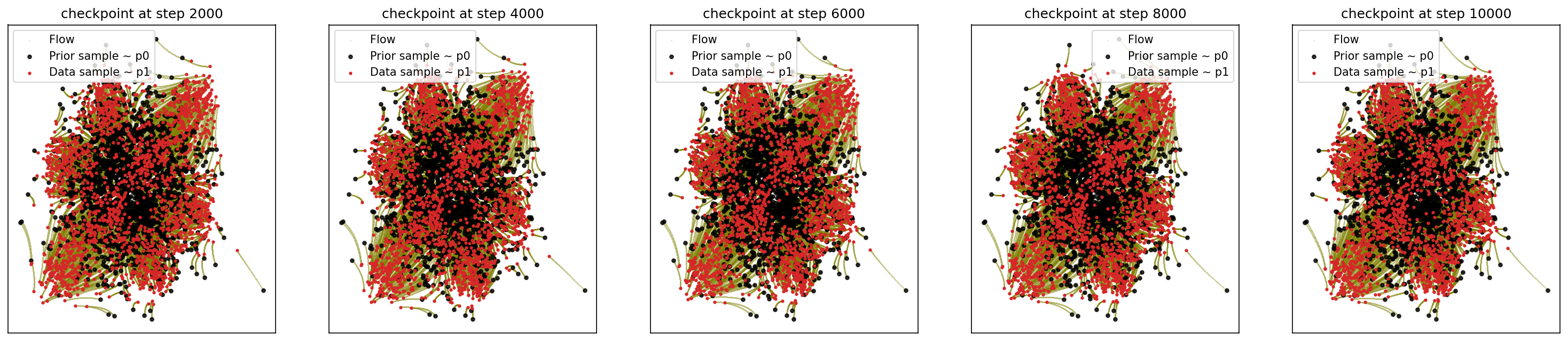
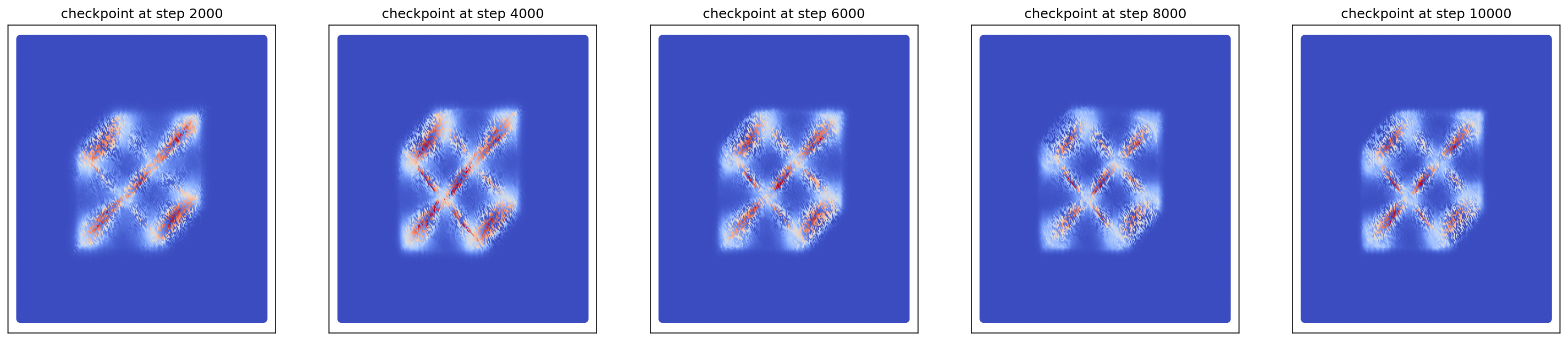
3.4 Generating 8-Gaussians
cfm_wrapper(sample_noise, sample_8_gaussians, pt_sampler=sample_conditional_pt_SB, vector_field=conditional_vector_field_SB, ot_sampler=OTPlanSampler(), n_steps=10000, likelihood=True)
# loss ~ 0.023
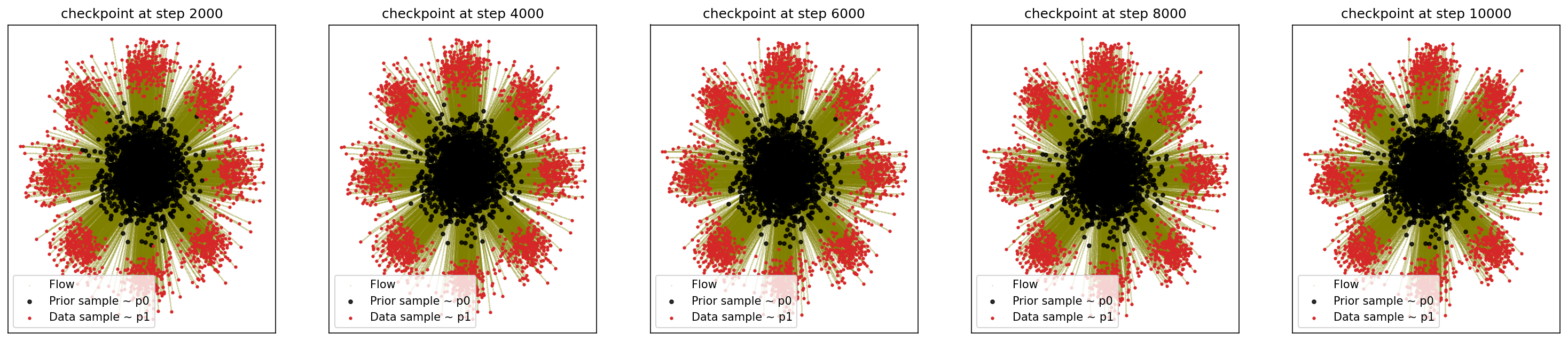
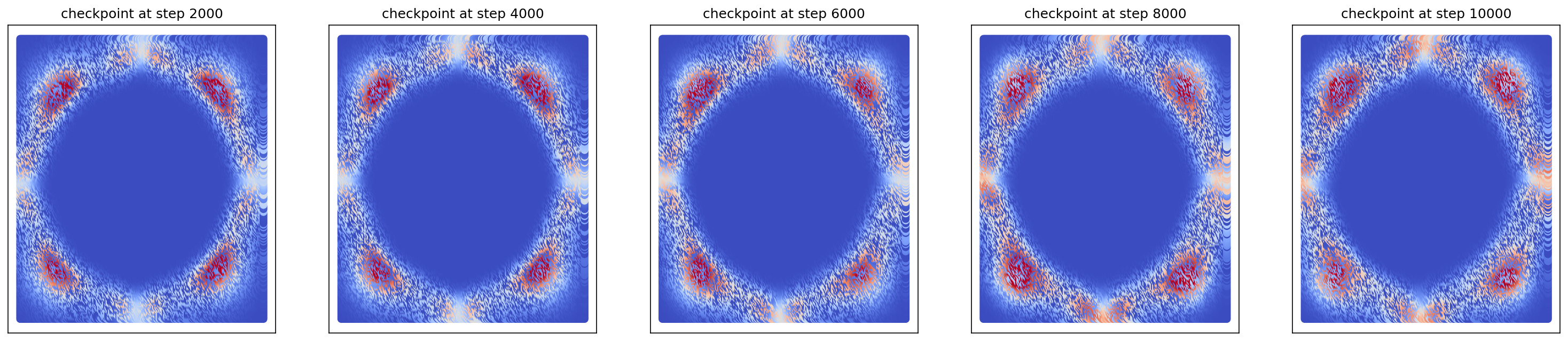
So, we can see that OT improves the training with much smaller loss converged and the probability calculation stabilizes in 2 checkpoints (4000 epochs).
4. Score + Flow Matching, SF2M
Here, we cannot use cfm_wrapper but the difference is minimal, just add a score matching term.
# Let's try using SF2M: Score + Flow matching
import torchsde
# the pt and flow field are the same as the SB case but here we add a score model to fit the scores from pt
# additionally, we will need a lambda(t) for the score scaling
def sample_conditional_pt_SB_noise(x0, x1, t, sigma=1.0):
'''
Draw a sample from N(mu_t(x0, x1), sigma), where
mu_t(x0, x1) = t * x1 + (1 - t) * x0 being the interpolation between x0 and x1
sigma_t^2 = t * (1-t) * sigma^2
'''
assert x0.shape == x1.shape
assert t.shape[0] == x0.shape[0]
t = t[..., None]
mu_t = t * x1 + (1. - t) * x0
sigma_t = sigma * torch.sqrt(t * (1. - t))
epsilon = torch.randn_like(x0)
return mu_t + sigma_t * epsilon, epsilon
# lambda(t)
def lamb(t, sigma=1.0):
t = t[..., None]
sigma_t = sigma * torch.sqrt(t * (1. - t))
return 2 * sigma_t / (sigma ** 2 + 1e-8)
# wrap the flow and score in a module
class SDE(torch.nn.Module):
noise_type = 'diagonal'
sde_type = 'ito'
def __init__(self, flow, score, input_size=(3, 32, 32), sigma=1.0):
super(SDE, self).__init__()
self.flow = flow
self.score = score
self.input_size = input_size
self.sigma = sigma
def f(self, t, y):
y = y.view(-1, *self.input_size)
if len(t.shape) == len(y.shape):
x = torch.cat([y, t], dim=1)
else:
x = torch.cat([y, t.repeat(y.shape[0])[:, None]], dim=1)
return self.flow(x).flatten(start_dim=1) + self.score(x).flatten(start_dim=1)
def g(self, t, y):
return torch.ones_like(y) * self.sigma * 5.0 # can be used to tune the noise, like diffusion
And we construct a SF2M wrapper:
def sf2m_wrapper(p0_sampler, p1_sampler, batch_size=1024, n_steps=10000):
# Everything the same, just add score matching part
ot_sampler = OTPlanSampler()
# some parameters
sigma = 0.1 # sigma_t = sigma = 0.1 a small constant value
dim = 2
n_checkpoints = 5
model = MLP(dim=dim, time_varying=True).to(DEVICE)
score_model = MLP(dim=dim, time_varying=True).to(DEVICE)
# using both model weights, equivalent to training them individually
optimizer = torch.optim.AdamW(list(model.parameters()) + list(score_model.parameters()))
flow_checkpoints = []
score_checkpoints = []
pbar = tqdm(range(n_steps + 1))
for k in pbar:
# sample prior = gaussian, posterior = moons
x0 = p0_sampler(batch_size).to(DEVICE)
x1 = p1_sampler(batch_size).to(DEVICE)
# match rows using OT plan
x0, x1 = ot_sampler.sample_plan(x0, x1)
# sample time
t = torch.rand(x0.shape[0], dtype=x0.dtype, device=DEVICE)
# generate some noisy x_t in between
xt, ep = sample_conditional_pt_SB_noise(x0, x1, t, sigma=sigma)
# conditional flow vector field
ut = conditional_vector_field_SB(x0, x1, t, xt)
# the model input is the noisy point xt and time
# the model output is the flow to matching that of ut
vt = model(torch.cat([xt, t[..., None]], dim=-1))
st = score_model(torch.cat([xt, t[..., None]], dim=-1)) # score
# loss is the flow matching loss
flow_loss = ((vt - ut) ** 2).mean()
score_loss = ((lamb(t) * st + ep) ** 2).mean()
loss = flow_loss + score_loss
# normal pytorch stuff
optimizer.zero_grad()
loss.backward()
optimizer.step()
if k % 100 == 0: pbar.set_description(f'Training step {k:06d}, loss = {loss.item():.3f}')
if (k > 0) and (k % (n_steps // n_checkpoints) == 0):
flow_checkpoints.append(copy.deepcopy(model))
score_checkpoints.append(copy.deepcopy(score_model))
## sample using the flow model only:
prior_samples = p0_sampler(1024).to(DEVICE)
trajs = sampling(prior_samples, flow_checkpoints)
plot_trajs(trajs, n_steps=n_steps)
## Sample using flow + score models
trajs = []
for flow_checkpoint, score_checkpoint in tqdm(zip(flow_checkpoints, score_checkpoints), desc='sample from checkpoint'):
sde = SDE(flow_checkpoint, score_checkpoint, input_size=(2,), sigma=sigma)
with torch.no_grad():
ts = torch.linspace(0, 1, 100, device=DEVICE)
traj = torchsde.sdeint(sde, x0, ts=ts, method='srk')
trajs.append(traj.cpu().numpy())
plot_trajs(trajs, n_steps=n_steps)
return None
4-1. 8-Gaussian to Moon
sf2m_wrapper(sample_8_gaussians, sample_moons, n_steps=10000)
# loss ~ 1.074
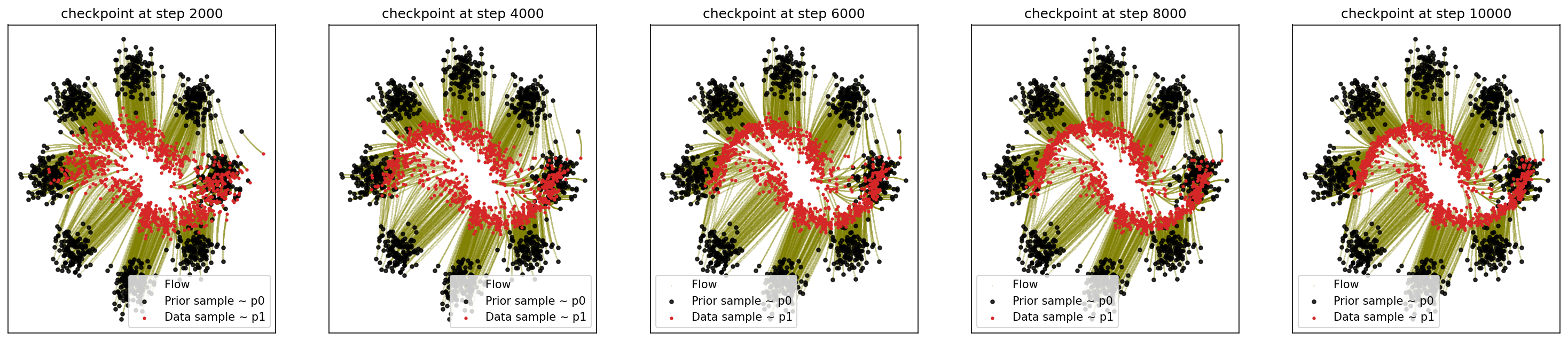
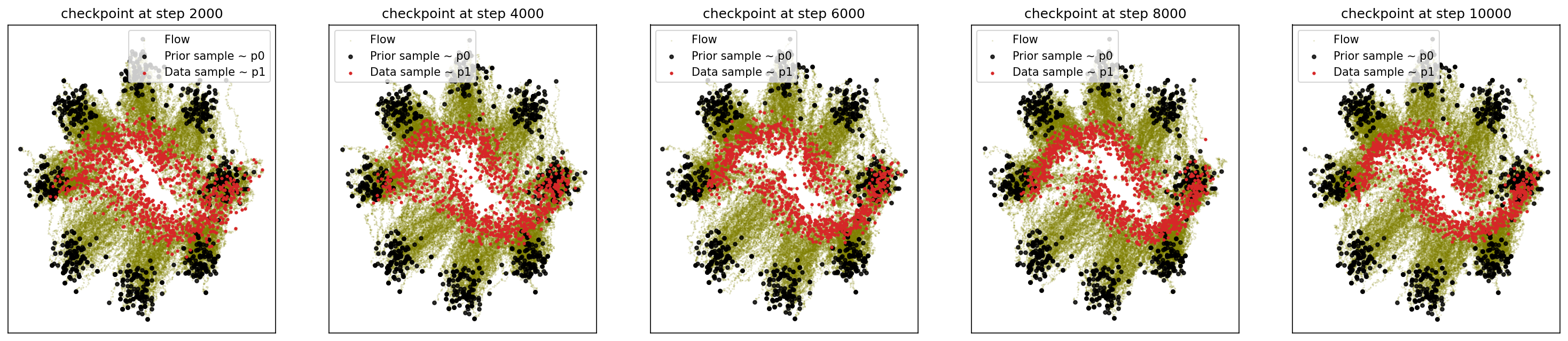
4-2. Generating Moon
sf2m_wrapper(sample_noise, sample_moons, n_steps=10000)
# loss ~ 1.037
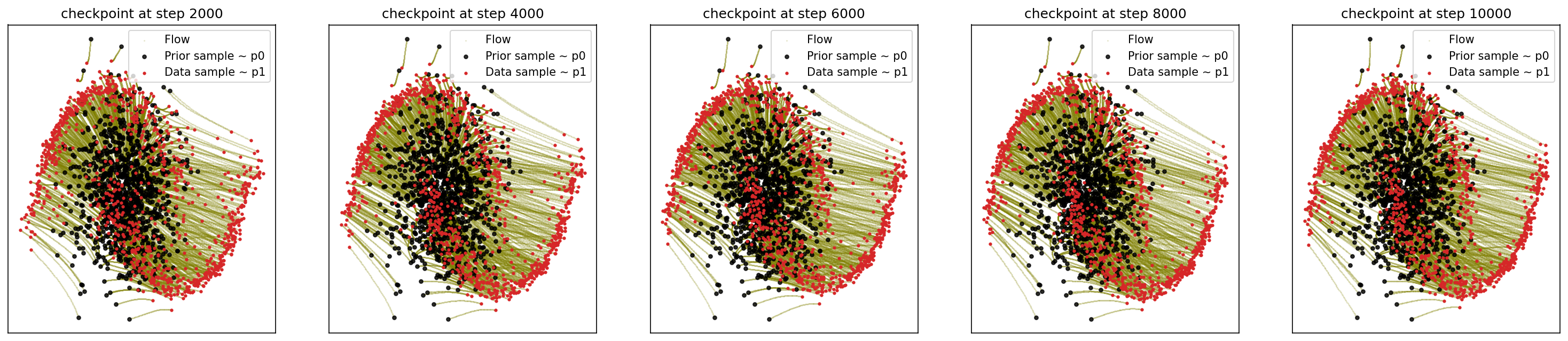
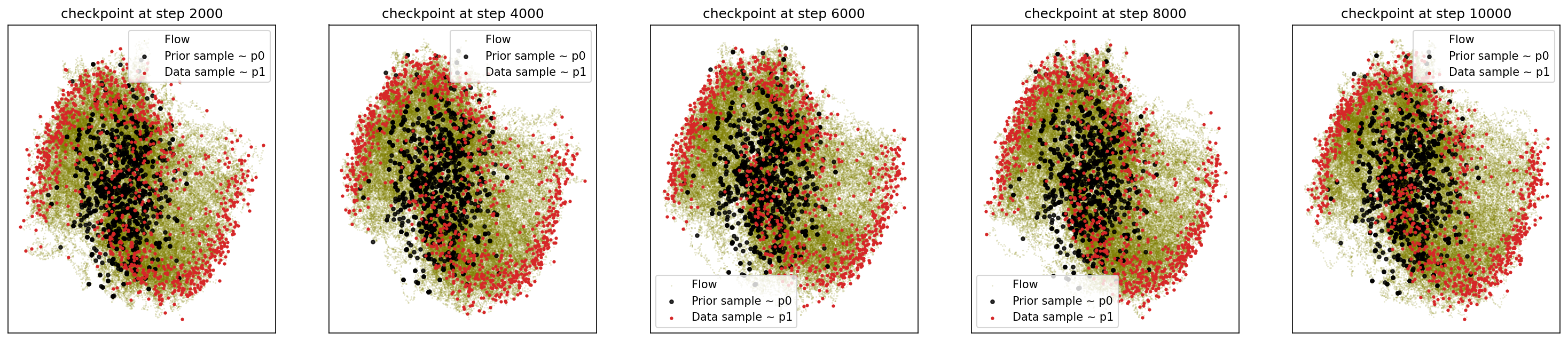
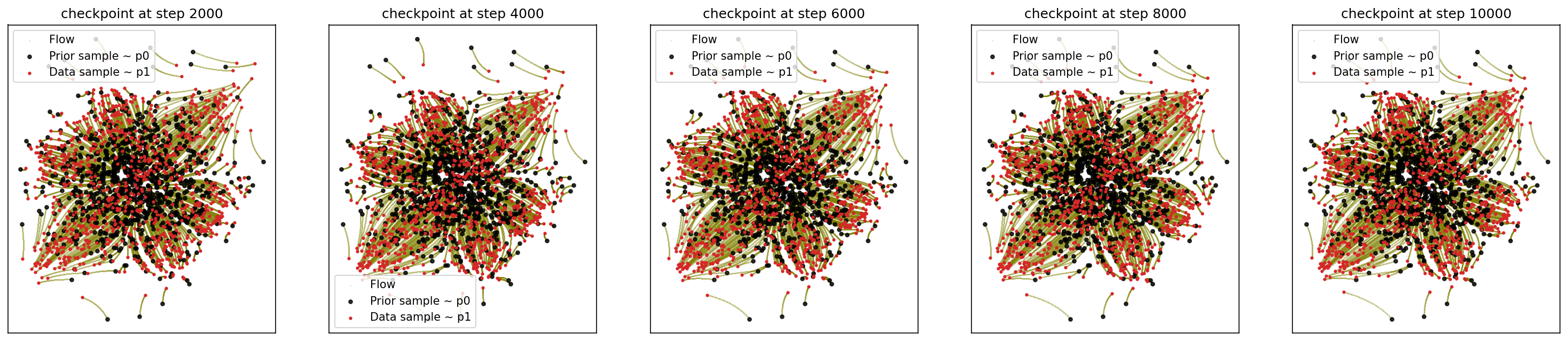
4-3. Generating Checkerboard
sf2m_wrapper(sample_noise, sample_checkerboard_data, n_steps=10000)
# loss ~ 1.031
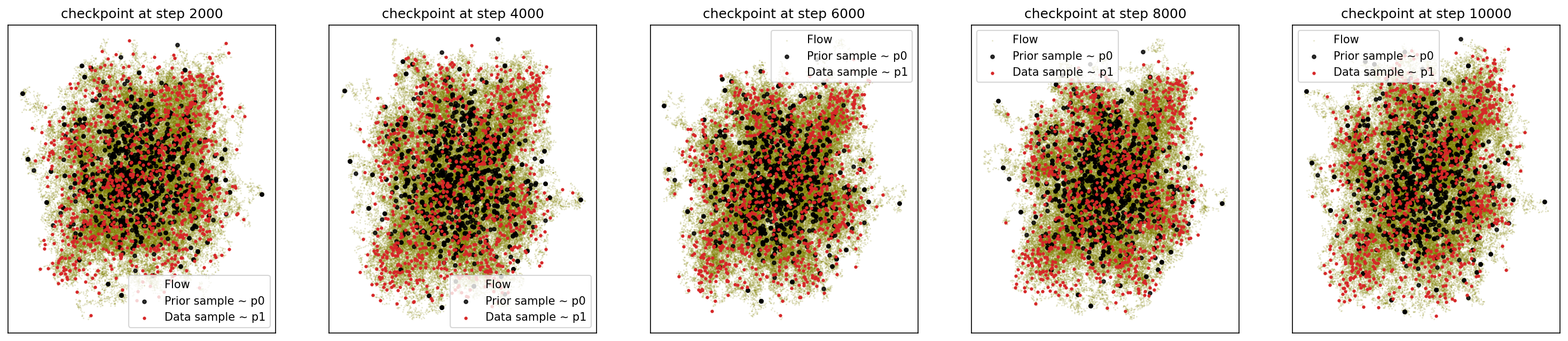
4-4. Generating 8-Gaussians
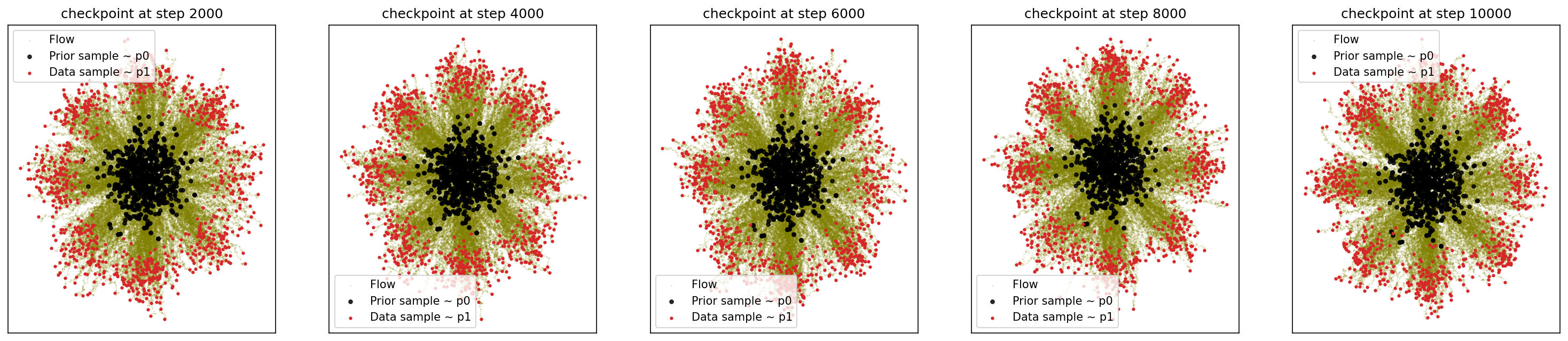
sf2m_wrapper(sample_noise, sample_8_gaussians, n_steps=10000)
# loss ~ 1.051
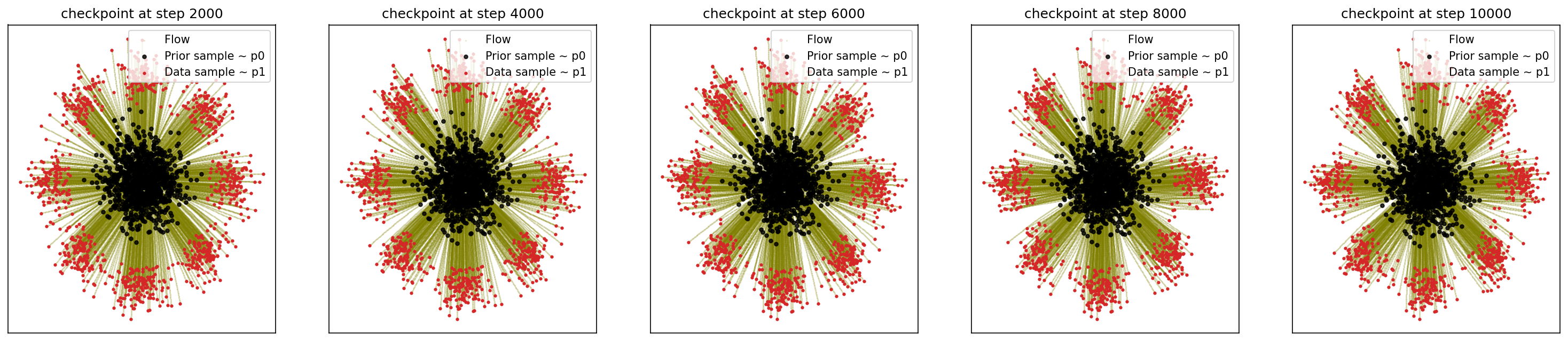
This gets a bit longer that expected. The image case will be in a separate post.
References
- Lipman et al, Flow Matching for Generative Modeling, (link)
- Lipman et al, Flow Matching Guide and Code, (link)
- Tong et al, Improving and generalizing flow-based generative models with minibatch optimal transport (link)
- Tong et al, Simulation-free Schrodinger bridges via score and flow matching (link)
- TorchCFM
- Flow-Matching