Discrete Flow Matching
We will explore the generative discrete flow matching model on 2D Checkerboard and Sequence data.
One benefit of DFM is to compute the ELBO or log-probability for any given data, by forward solving ODE using the trained model.
This notebook is the standalone version for future references.
Table of Contents:
-
Discrete Frameworks
1.1 Scheduler
1.2 Mixture of discrete paths
1.3 Training losses
1.4 ODE/SDE solvers for DFM
- Training Pipeline
- ELBO estimates
The above will be applied to 2 cases: 2D and Sequence
%load_ext autoreload
%autoreload 2
import os, time, torch, einops, copy
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from torch import Tensor
from abc import ABC, abstractmethod
from typing import Union, Optional, Callable
from dataclasses import dataclass
from contextlib import nullcontext
from math import ceil
from tqdm import tqdm
assert torch.cuda.is_available()
device = torch.device('cuda')
SAVE_PATH = 'discrete_flow/'
os.makedirs(SAVE_PATH, exist_ok=True)
1. Discrete Frameworks
In the continuous case, at train time we do the following:
- Sample \(t\in[0,1]\)
- Sample data point \(x_1\sim q(x)\)
-
Sample $$x \sim p_t(x x_1)\(given some\)p_t$$ -
Compute corresponding vector field $$u_t(x x_1)$$ - Use neural network \(v_{t,\theta}(x)\) to regress on the vector field
In the discrete case, steps 1-2 remain and we need to massage the following steps:
- Sample \(x \sim p_t(x\|x_1)\) given some \(p_t\) using mixture of discrete path.
4-5. Instead of regress on the flow vector field, we predict the \(x_1\) given \(x_t\) with typical cross-entropy loss or generalized KL-loss.
We first take a look at the schedulers, which are identical to the continuous case. The scheduler holds the time-dependent mean \(\alpha_t\) and variance \(\sigma_t\) that models the normal distribution
\[p_t(x|x_1)\sim\mathcal{N}(x| \alpha_t x_1, \sigma_t^2I)\]Again, \(\alpha_t\) and \(\sigma_t\) need to satisfy the boundary condition: \(\alpha_1 = \sigma_0 = 1\) and \(\alpha_0 = \sigma_1 = 0\)
In the continuous case, the source distribution, \(p_0\) is usually signal-less by design to be a normal Gaussian distribution. In the discrete case, the source distribution at each position can be 2 cases:
- Uniform distribution over the discrete space or the vocabularies.
- Mask token
Both source distributions provide signal-less and can be coupled with data distribution via any schedulers.
1.1 Scheduler
@dataclass
class SchedulerOutput:
alpha_t: Tensor
sigma_t: Tensor
d_alpha_t: Tensor
d_sigma_t: Tensor
class Scheduler(ABC):
'''Scheduler Base
p_t(x | x_1) = N(x | alpha_t * x_1, sigma_t^2 * I)
'''
@abstractmethod
def __call__(self, t: Tensor) -> SchedulerOutput:
pass
class ConditionalOTScheduler(Scheduler):
'''Conditional OT Scheduler
p_t(x | x_1) = N(x | t x_1, (1-t)^2 I)
'''
def __call__(self, t: Tensor) -> SchedulerOutput:
return SchedulerOutput(alpha_t=t,
sigma_t=1 - t,
d_alpha_t=torch.ones_like(t),
d_sigma_t=-torch.ones_like(t))
class PolynomialScheduler(Scheduler):
'''Polynomial Scheduler
p_t(x | x_1) = N(x | t^n x_1, (1-t^n)^2 I)
'''
def __init__(self, n: Union[float, int]) -> None:
assert isinstance(n, (float, int))
assert n > 0.0
self.n = n
def __call__(self, t: Tensor) -> SchedulerOutput:
n = self.n
return SchedulerOutput(alpha_t=t ** n,
sigma_t=1 - t ** n,
d_alpha_t=n * (t ** (n - 1)),
d_sigma_t=-n * (t ** (n - 1)))
class CosineScheduler(Scheduler):
'''Cosine Scheduler
p_t(x | x_1) = N(x | sin(pi*t/2) x_1, cos(pi*t/2)^2 I)
'''
def __call__(self, t: Tensor) -> SchedulerOutput:
pi = torch.pi
return SchedulerOutput(alpha_t=torch.sin(0.5 * pi * t),
sigma_t=torch.cos(0.5 * pi * t),
d_alpha_t=0.5 * pi * torch.cos(0.5 * pi * t),
d_sigma_t=-0.5 * pi * torch.sin(0.5 * pi * t))
1.2 Mixture of Discrete Path
We denote a sequence \(x\) as an array with \(N\) element: \(x = (x_1, x_2, x_3, ..., x_N)\) where each element takes on discrete value from a set of vocabulary of size \(d\). The sequence space is then \(d^N\).
Given samples from source and target distributions, \(x_0\) and \(x_1\), and any data coupling \(\pi(x_0, x_1)\), the probability path \(p_t\) can be represented with marginal probability paths:
\[p_t(x) = \sum_{x_0, x_1}p_t(x \mid x_0, x_1)\pi(x_0, x_1)\]Since \(x\) is an N-dim array, we can further represent the marginal probability paths using the mixture of its individual components:
\[p_t(x|x_0, x_1) = \prod_{i=1}^N p_t(x^i \mid x_0, x_1)\]\(p_t(x^i \mid x_0, x_1)\) is a time-dependent probability on the vocabulary set with boundary conditions defined by the source and target:
\[p_0(x^i \mid x_0, x_1) = \delta_{x_0}(x^i)\] \[p_1(x^i \mid x_0, x_1) = \delta_{x_1}(x^i)\]where \(\delta_y(x^i) = 1\) if \(x^i = y^i\) and \(0\) otherwise.
Then we can use a convex linear combination (similar to those in continuous case) to represent the individual one of a mixture of discrete paths:
\[p_t(x^i \mid x_0, x_1) = (1-\kappa_t)p_0(x^i \mid x_0, x_1) + \kappa_t p_1(x^i \mid x_0, x_1) = (1-\kappa_t)\delta_{x_0}(x^i) + \kappa_t \delta_{x_1}(x^i)\]with \(0 < \kappa_t < 1\), \(\kappa_0 = 0\), \(\kappa_1 = 1\) and monotonically increasing.
This individual marginal probability path for position \(i\) indicates that given time \(t\) and \(x_0\) and \(x_1\), \(x^i\) only got 2 choices: \(x_0^i\) with probability \(\kappa_t\) and \(x_1^i\) with probability \(1-\kappa_t\), i.e. \(x_i\) assumes either the source or target with time-dependent probability.
The conditional marginal generating (forward) velocity is then
\[u_t^i(x^i \mid z) = \frac{\dot{\kappa_t}}{1 - \kappa_t}\left[p_{1 \mid t}(x^i|z) - \delta_z(x^i) \right]\](See Gat. et al 2024 for derivation)
This velocity is used then the model is trained to be the denoiser (as compared to noise-prediction.) The \(\kappa_t\) is from the scheduler and \(p_{1 \mid t}(x^i \mid x)\) is the posterior probability defined on the vocabulary set of size \(d\). Essentially, this is from the trained neural network given noised sequence \(x_t\) at time \(t\) and predicting the posterior of the clean sequence \(x_1\). \(\delta_z(x^i)\) is the one-hot probability of \(x_t\). So this velocity makes \(x_t\) move toward predicted \(x_1\) at sampling. Note that \(\kappa_t = 1\) when \(t=1\) is a singularity for the generating velocity, so we typically do the sampling till \(t = 1-\epsilon\) and use \(p_{1 \mid t=1-\epsilon}(x^i \mid x)\) as the sample at \(x_1\).
The reverse velocity is then
\[u_t^i(x^i \mid z) = \frac{\dot{\kappa_t}}{\kappa_t}\left[\delta_z(x^i) - p_{0 \mid t}(x^i \mid x) \right]\]which will be used for corrector sampling during the generating/inferencing process.
def unsqueeze_to_match(source: Tensor, target: Tensor, how: str = "suffix") -> Tensor:
"""
Unsqueeze the source tensor to match the dimensionality of the target tensor.
Args:
source (Tensor): The source tensor to be unsqueezed.
target (Tensor): The target tensor to match the dimensionality of.
how (str, optional): Whether to unsqueeze the source tensor at the beginning
("prefix") or end ("suffix"). Defaults to "suffix".
Returns:
Tensor: The unsqueezed source tensor.
"""
assert (
how == "prefix" or how == "suffix"
), f"{how} is not supported, only 'prefix' and 'suffix' are supported."
dim_diff = target.dim() - source.dim()
for _ in range(dim_diff):
if how == "prefix":
source = source.unsqueeze(0)
elif how == "suffix":
source = source.unsqueeze(-1)
return source
def expand_tensor_like(input_tensor: Tensor, expand_to: Tensor) -> Tensor:
"""`input_tensor` is a 1d vector of length equal to the batch size of `expand_to`,
expand `input_tensor` to have the same shape as `expand_to` along all remaining dimensions.
Args:
input_tensor (Tensor): (batch_size,).
expand_to (Tensor): (batch_size, ...).
Returns:
Tensor: (batch_size, ...).
"""
assert input_tensor.ndim == 1, "Input tensor must be a 1d vector."
assert (
input_tensor.shape[0] == expand_to.shape[0]
), f"The first (batch_size) dimension must match. Got shape {input_tensor.shape} and {expand_to.shape}."
dim_diff = expand_to.ndim - input_tensor.ndim
t_expanded = input_tensor.clone()
t_expanded = t_expanded.reshape(-1, *([1] * dim_diff))
return t_expanded.expand_as(expand_to)
@dataclass
class PathSample:
'''Sample of conditional probability path'''
x_1: Tensor
x_0: Tensor
t: Tensor
x_t: Tensor
dx_t: Tensor
@dataclass
class DiscretePathSample:
'''Sample of conditional discrete probability path'''
x_1: Tensor
x_0: Tensor
t: Tensor
x_t: Tensor
class ProbPath(ABC):
'''Probability Path Base Class'''
@abstractmethod
def sample(self, x_0: Tensor, x_1: Tensor, t: Tensor) -> PathSample:
pass
def assert_sample_shape(self, x_0: Tensor, x_1: Tensor, t: Tensor) -> None:
assert t.ndim == 1
assert t.shape[0] == x_0.shape[0] == x_1.shape[0]
assert x_0.shape == x_1.shape
# mixture discrete path
class MixtureDiscreteProbPath(ProbPath):
'''Mixture Discrete Probability Path'''
def __init__(self, scheduler: Scheduler):
self.scheduler = scheduler
def sample(self, x_0: Tensor, x_1: Tensor, t: Tensor) -> DiscretePathSample:
self.assert_sample_shape(x_0, x_1, t)
sigma_t = self.scheduler(t).sigma_t
sigma_t = expand_tensor_like(sigma_t, x_1)
# sigma_t determines the probability to stay at source
# with probability of 1 - sigma_t it flips to target / data
source_indices = torch.rand(size=x_1.shape, device=x_1.device) < sigma_t
x_t = torch.where(source_indices, x_0, x_1)
return DiscretePathSample(x_1=x_1, x_0=x_0, t=t, x_t=x_t)
def posterior_to_velocity(self, posterior_logits: Tensor, x_t: Tensor, t: Tensor) -> Tensor:
# this is p_{1|t}(x|z)
posterior = torch.softmax(posterior_logits, dim=-1)
vocabulary_size = posterior.shape[-1]
# this is p_t(x|z)
x_t = torch.nn.functional.one_hot(x_t, num_classes=vocabulary_size)
t = unsqueeze_to_match(source=t, target=x_t)
scheduler_output = self.scheduler(t)
kappa_t = scheduler_output.alpha_t
d_kappa_t = scheduler_output.d_alpha_t
return (d_kappa_t / (1 - kappa_t)) * (posterior - x_t)
1.3 Training Losses
For training the probability denoiser, i.e. training a model that reproduces \(p_{1 \mid t}(x^i \mid z)\), the loss takes the form:
\[\mathcal{L}(\theta) = -\sum_i \textbf{E}_{t, (X_0, X_1), X_t}\left[\log{p_{1 \mid t}(X_1^i \mid X_t)} \right]\]This is essentially the cross entropy loss. The model is trained to predict the signal sequence \(X_1\) given some noised sequence of \(X_t\). In analogy to image, this is predicting the noise-less image \(X_1\) given some noised images \(X_t\) instead of predicting the flow vector field \(u_t(X_t)\)
Alternatively, we can use generalized KL loss, which takes the form:
\[\mathcal{L}(\theta) = -\sum_i \textbf{E}_{t, (X_0, X_1), X_t}\frac{\dot{\kappa_t}}{1-\kappa_t}\left[(\delta_{x_1}(x_t^i) - 1)\log{p_{1 \mid t}(x_1^i \mid x_t)} + \delta_{x_1}(x_t^i) - p_{1 \mid t}(x_1^i \mid x_t) \right]\]class MixturePathGeneralizedKL(torch.nn.modules.loss._Loss):
r"""A generalized KL loss for discrete flow matching.
A class that measures the generalized KL of a discrete flow model :math:`p_{1|t}` w.r.t. a probability path given by ``path``. Note: this class is assuming that the model is trained on the same path.
For a model trained on a space :math:`\mathcal{S} = \mathcal{T}^d`, :math:`\mathcal{T} = [K] = \set{1,2,\ldots,K}`, the loss is given by
.. math::
\ell_i(x_1, x_t, t) = -\frac{\dot{\kappa}_t}{1-\kappa_t} \biggr[ p_{1|t}(x_t^i|x_t) -\delta_{x^i_1}(x_t^i) + (1-\delta_{x^i_1}(x_t^i))\left(\log p_{1|t}(x_1^i|x_t)\right)\biggr],
where :math:`\kappa_t` is the scheduler associated with ``path``.
Args:
path (MixtureDiscreteProbPath): Probability path (x-prediction training).
reduction (str, optional): Specify the reduction to apply to the output ``'none'`` | ``'mean'`` | ``'sum'``. ``'none'``: no reduction is applied to the output, ``'mean'``: the output is reduced by mean over sequence elements, ``'sum'``: the output is reduced by sum over sequence elements. Defaults to 'mean'.
"""
def __init__(self, path: MixtureDiscreteProbPath, reduction: str = "mean") -> None:
super().__init__(None, None, reduction)
self.path = path
def forward(self, logits: Tensor, x_1: Tensor, x_t: Tensor, t: Tensor) -> Tensor:
r"""Evaluates the generalized KL loss.
Args:
logits (Tensor): posterior model output (i.e., softmax(``logits``) :math:`=p_{1|t}(x|x_t)`), shape (batch, d, K).
x_1 (Tensor): target data point :math:`x_1 \sim q`, shape (batch, d).
x_t (Tensor): conditional sample at :math:`x_t \sim p_t(\cdot|x_1)`, shape (batch, d).
t (Tensor): times in :math:`[0,1]`, shape (batch).
Raises:
ValueError: reduction value must be one of ``'none'`` | ``'mean'`` | ``'sum'``.
Returns:
Tensor: Generalized KL loss.
"""
x_1_shape = x_1.shape
# extract x_1 value of log(p_{1|t}(x|x_t)).
log_p_1t = torch.log_softmax(logits, dim=-1)
log_p_1t_x1 = torch.gather(log_p_1t, dim=-1, index=x_1.unsqueeze(-1))
log_p_1t_x1 = log_p_1t_x1.view(*x_1_shape)
# extract x_t value of p_{1|t}(x|x_t).
p_1t = torch.exp(log_p_1t)
p_1t_xt = torch.gather(p_1t, dim=-1, index=x_t.unsqueeze(-1))
p_1t_xt = p_1t_xt.view(*x_1_shape)
scheduler_output = self.path.scheduler(t)
jump_coefficient = (scheduler_output.d_alpha_t / (1 - scheduler_output.alpha_t))[(...,) + (None,) * (x_1.dim() - 1)]
jump_coefficient = jump_coefficient.repeat(1, *x_1_shape[1:])
delta_x1_xt = (x_t == x_1).to(log_p_1t.dtype)
loss = -jump_coefficient * (p_1t_xt - delta_x1_xt + (1 - delta_x1_xt) * log_p_1t_x1)
if self.reduction == "mean":
return torch.mean(loss)
elif self.reduction == "sum":
return torch.sum(loss)
elif self.reduction == "none":
return loss
else:
raise ValueError(f"{self.reduction} is not a valid value for reduction")
1.4 ODE/SDE Solvers
def categorical(probs: Tensor) -> Tensor:
r"""Categorical sampler according to weights in the last dimension of ``probs`` using :func:`torch.multinomial`.
Args:
probs (Tensor): probabilities.
Returns:
Tensor: Samples.
"""
return torch.multinomial(probs.flatten(0, -2), 1, replacement=True).view(*probs.shape[:-1])
def get_nearest_times(time_grid: Tensor, t_discretization: Tensor) -> Tensor:
distances = torch.cdist(
time_grid.unsqueeze(1),
t_discretization.unsqueeze(1),
compute_mode="donot_use_mm_for_euclid_dist",
)
nearest_indices = distances.argmin(dim=1)
return t_discretization[nearest_indices]
# model wrapper for the solvers
class ModelWrapper(ABC, torch.nn.Module):
"""
This class is used to wrap around another model, adding custom forward pass logic.
"""
def __init__(self, model: torch.nn.Module):
super().__init__()
self.model = model
def forward(self, x: Tensor, t: Tensor, **extras) -> Tensor:
return self.model(x=x, t=t, **extras)
class Solver(ABC, torch.nn.Module):
"""Abstract base class for solvers."""
@abstractmethod
def sample(self, x_0: Tensor = None) -> Tensor:
pass
class MixtureDiscreteSolver(Solver):
def __init__(
self,
model: ModelWrapper,
path: MixtureDiscreteProbPath,
vocabulary_size: int,
source_distribution_p: Optional[Tensor] = None,
solver_type: str = 'Euler'
):
super().__init__()
self.model = model
self.path = path
self.vocabulary_size = vocabulary_size
if source_distribution_p is not None:
assert source_distribution_p.shape == torch.Size(
[vocabulary_size]
), f"Source distribution p dimension must match the vocabulary size {vocabulary_size}. Got {source_distribution_p.shape}."
self.source_distribution_p = source_distribution_p
assert solver_type in ['Euler', 'Heun']
self.solver_type = solver_type
@torch.no_grad()
def sample(
self,
x_init: Tensor,
step_size: Optional[float],
div_free: Union[float, Callable[[float], float]] = 0.0,
dtype_categorical: torch.dtype = torch.float32,
time_grid: Tensor = torch.tensor([0.0, 1.0]),
return_intermediates: bool = False,
verbose: bool = False,
**model_extras,
) -> Tensor:
if not div_free == 0.0:
assert (self.source_distribution_p is not None), "Source distribution p must be specified in order to add a divergence-free term to the probability velocity."
# Initialize the current state `x_t` with the initial state `X_0`.
time_grid = time_grid.to(device=x_init.device)
if step_size is None:
# If step_size is None then set the t discretization to time_grid.
t_discretization = time_grid
n_steps = len(time_grid) - 1
else:
# If step_size is float then t discretization is uniform with step size set by step_size.
t_init = time_grid[0].item()
t_final = time_grid[-1].item()
assert (t_final - t_init) > step_size, f"Time interval [time_grid[0], time_grid[-1]] must be larger than step_size. Got a time interval [{t_init}, {t_final}] and step_size {step_size}."
n_steps = ceil((t_final - t_init) / step_size)
t_discretization = torch.tensor([t_init + step_size * i for i in range(n_steps)] + [t_final], device=x_init.device)
if return_intermediates:
# get order of intermediate steps:
order = torch.argsort(time_grid)
# Compute intermediate steps to return via nearest points in t_discretization to time_grid.
time_grid = get_nearest_times(time_grid=time_grid, t_discretization=t_discretization)
x_t = x_init.clone()
steps_counter = 0
res = []
if return_intermediates:
res = [x_init.clone()]
if verbose:
ctx = tqdm(total=t_final, desc=f"NFE: {steps_counter}")
else:
ctx = nullcontext()
with ctx:
for i in range(n_steps):
t = t_discretization[i : i + 1]
h = t_discretization[i + 1 : i + 2] - t_discretization[i : i + 1]
# Sample x_1 ~ p_1|t( \cdot |x_t)
p_1t = self.model(x=x_t, t=t.repeat(x_t.shape[0]), **model_extras)
x_1 = categorical(p_1t.to(dtype=dtype_categorical))
# Checks if final step
if i == n_steps - 1: x_t = x_1
else:
# Compute u_t(x|x_t,x_1)
scheduler_output = self.path.scheduler(t=t)
k_t = scheduler_output.alpha_t
d_k_t = scheduler_output.d_alpha_t
delta_1 = torch.nn.functional.one_hot(x_1, num_classes=self.vocabulary_size).to(k_t.dtype)
u = d_k_t / (1 - k_t) * delta_1
# Add divergence-free part
div_free_t = div_free(t) if callable(div_free) else div_free
if div_free_t > 0:
p_0 = self.source_distribution_p[(None,) * x_t.dim()]
u = u + div_free_t * d_k_t / (k_t * (1 - k_t)) * ((1 - k_t) * p_0 + k_t * delta_1)
# Set u_t(x_t|x_t,x_1) = 0
delta_t = torch.nn.functional.one_hot(x_t, num_classes=self.vocabulary_size)
u = torch.where(delta_t.to(dtype=torch.bool), torch.zeros_like(u), u)
# Sample x_t ~ u_t( \cdot |x_t,x_1) -- predictor
intensity = u.sum(dim=-1) # Assuming u_t(xt|xt,x1) := 0
mask_jump = torch.rand(size=x_t.shape, device=x_t.device) < 1 - torch.exp(-h * intensity)
if mask_jump.sum() > 0:
x_t[mask_jump] = categorical(u[mask_jump].to(dtype=dtype_categorical))
#### the following is only for Heun method
if self.solver_type == 'Heun':
x_th = x_t.clone()
th = t + h
p_1th = self.model(x=x_th, t=th.repeat(x_th.shape[0]), **model_extras)
x_1th = categorical(p_1th.to(dtype=dtype_categorical))
scheduler_output_th = self.path.scheduler(t=th)
k_th = scheduler_output_th.alpha_t
d_k_th = scheduler_output_th.d_alpha_t
delta_1th = torch.nn.functional.one_hot(x_1th, num_classes=self.vocabulary_size).to(k_th.dtype)
u_th = d_k_th / (1 - k_th) * delta_1th
# Add divergence-free part
div_free_th = div_free(th) if callable(div_free) else div_free
if div_free_th > 0:
p_0 = self.source_distribution_p[(None,) * x_th.dim()]
u_th = u_th + div_free_th * d_k_th / (k_th * (1 - k_th)) * ((1 - k_th) * p_0 + k_th * delta_1th)
# Set u_t(x_t|x_t,x_1) = 0
delta_th = torch.nn.functional.one_hot(x_th, num_classes=self.vocabulary_size)
u_th = torch.where(delta_th.to(dtype=torch.bool), torch.zeros_like(u_th), u_th)
# combine u and u_{t+h} -- corrector
u = 0.5 * (u + u_th)
intensity = u.sum(dim=-1)
mask_jump = torch.rand(size=x_t.shape, device=x_t.device) < 1 - torch.exp(-h * intensity)
if mask_jump.sum() > 0:
x_t[mask_jump] = categorical(u[mask_jump].to(dtype=dtype_categorical))
steps_counter += 1
t = t + h
if return_intermediates and (t in time_grid):
res.append(x_t.clone())
if verbose:
ctx.n = t.item()
ctx.refresh()
ctx.set_description(f"NFE: {steps_counter}")
if return_intermediates:
if step_size is None:
return torch.stack(res, dim=0)
else:
return torch.stack(res, dim=0)[order]
else:
return x_t
class SimpleSolver(Solver):
def __init__(self,
model: ModelWrapper,
path: MixtureDiscreteProbPath,
vocabulary_size: int,
solver_type: str = 'Euler',
stochastic: bool = False,
source_distribution: bool = 'uniform'
):
super().__init__()
self.model = model
self.path = path
self.vocabulary_size = vocabulary_size
self.solver_type = solver_type
self.stochastic = stochastic
self.source_distribution = source_distribution
@torch.no_grad()
def sample(
self,
x_init: Tensor,
step_size: Optional[float],
dtype_categorical: torch.dtype = torch.float32,
time_grid: Tensor = torch.tensor([0.0, 1.0]),
return_intermediates: bool = False,
verbose: bool = False,
**model_extras,
) -> Tensor:
# Initialize the current state `x_t` with the initial state `X_0`.
time_grid = time_grid.to(device=x_init.device)
if step_size is None:
# If step_size is None then set the t discretization to time_grid.
t_discretization = time_grid
n_steps = len(time_grid) - 1
else:
# If step_size is float then t discretization is uniform with step size set by step_size.
t_init = time_grid[0].item()
t_final = time_grid[-1].item()
assert (t_final - t_init) > step_size, f"Time interval [time_grid[0], time_grid[-1]] must be larger than step_size. Got a time interval [{t_init}, {t_final}] and step_size {step_size}."
n_steps = ceil((t_final - t_init) / step_size)
t_discretization = torch.tensor([t_init + step_size * i for i in range(n_steps)] + [t_final], device=x_init.device)
if return_intermediates:
# get order of intermediate steps:
order = torch.argsort(time_grid)
# Compute intermediate steps to return via nearest points in t_discretization to time_grid.
time_grid = get_nearest_times(time_grid=time_grid, t_discretization=t_discretization)
x_t = x_init.clone()
steps_counter = 0
res = []
if return_intermediates:
res = [x_init.clone()]
if verbose:
ctx = tqdm(total=t_final, desc=f"NFE: {steps_counter}")
else:
ctx = nullcontext()
with ctx:
for i in range(n_steps):
t = t_discretization[i : i + 1]
h = t_discretization[i + 1 : i + 2] - t_discretization[i : i + 1]
# Sample x_1 ~ p_1|t( \cdot |x_t)
p_1t = self.model(x=x_t, t=t.repeat(x_t.shape[0]), **model_extras)
x_1 = categorical(p_1t.to(dtype=dtype_categorical))
# Checks if final step
if i == n_steps - 1: x_t = x_1
else:
# kappa
scheduler_output = self.path.scheduler(t=t)
k_t = scheduler_output.alpha_t
d_k_t = scheduler_output.d_alpha_t
# PMFs
p_1t = torch.softmax(p_1t, dim=-1)
delta_t = torch.nn.functional.one_hot(x_t, num_classes=self.vocabulary_size)
delta_1 = torch.nn.functional.one_hot(x_1, num_classes=self.vocabulary_size)
# velocity
u_t = d_k_t / (1 - k_t) * delta_1 #+ s_t * delta_n
# Euler point
p_t = delta_t + h * u_t
### Start Heun
if self.solver_type == 'Heun':
x_th = categorical(p_t.to(dtype=dtype_categorical))
th = t + h
p_1th = self.model(x=x_th, t=th.repeat(x_t.shape[0]), **model_extras)
x_1th = categorical(p_1th.to(dtype=dtype_categorical))
# kappa
scheduler_output = self.path.scheduler(t=th)
k_th = scheduler_output.alpha_t
d_k_th = scheduler_output.d_alpha_t
# PMFs
p_1t = torch.softmax(p_1th, dim=-1)
delta_th = torch.nn.functional.one_hot(x_th, num_classes=self.vocabulary_size)
delta_1th = torch.nn.functional.one_hot(x_1th, num_classes=self.vocabulary_size)
u_th = d_k_th / (1 - k_th) * delta_1th
# Heun
p_t = delta_t + 0.5 * h * (u_t + u_th)
### Start stochastic
if self.stochastic:
# noise PMFs with uniform
s_t = scheduler_output.sigma_t
if self.source_distribution == 'uniform':
x_n = torch.randint_like(x_t, 0, self.vocabulary_size)
elif self.source_distribution == 'mask':
x_n = (torch.zeros_like(x_t) + self.vocabulary_size - 1).long()
delta_n = torch.nn.functional.one_hot(x_n, num_classes=self.vocabulary_size)
p_t += delta_n * h * s_t ** 0.5
# Sample
x_t = categorical(p_t.to(dtype=dtype_categorical))
steps_counter += 1
t = t + h
if return_intermediates and (t in time_grid):
res.append(x_t.clone())
if verbose:
ctx.n = t.item()
ctx.refresh()
ctx.set_description(f"NFE: {steps_counter}")
if return_intermediates:
if step_size is None:
return torch.stack(res, dim=0)
else:
return torch.stack(res, dim=0)[order]
else:
return x_t
2. Training Pipeline
def train_discrete_flow_matching_model(model, path, x_1_gen_fn, loss_type='KL', source_distribution='uniform', model_prefix='test',
vocab_size=128, batch_size=4096, lr=0.001, iterations=30000, epsilon=1e-4, device=device):
assert loss_type in ['KL', 'CE']
assert source_distribution in ['uniform', 'mask']
prefix = f'{model_prefix} training {loss_type} loss with {source_distribution} distribution'
model_name = f'{model_prefix}_{loss_type}_{source_distribution}_it_{iterations:06d}'
if source_distribution == 'uniform':
added_token = 0
elif source_distribution == 'mask':
mask_token = vocab_size # tokens starting from zero
added_token = 1
# additional mask token
vocab_size += added_token
# model
model.train()
model.to(device)
# optimizer
optim = torch.optim.Adam(model.parameters(), lr=lr)
# loss function
if loss_type == 'KL':
loss_fn = MixturePathGeneralizedKL(path=path)
elif loss_type == 'CE':
loss_fn = torch.nn.CrossEntropyLoss()
# training loop
steps = 0
losses = []
pbar = tqdm(range(iterations + 1))
for i in pbar:
# sample data x_1
x_1 = x_1_gen_fn(n_grid_points=vocab_size - added_token, batch_size=batch_size, device=device) # sample data
# sample noise x_0
if source_distribution == 'uniform':
x_0 = torch.randint_like(x_1, high=vocab_size)
elif source_distribution == 'mask':
x_0 = torch.zeros_like(x_1) + mask_token
# sample time
t = torch.rand(x_1.shape[0]).to(device) * (1 - epsilon)
# sample probability path, in this case, (X_0,X_1) ~ pi(X_0,X_1) = p_0(X_0)p_1(X_1)
path_sample = path.sample(t=t, x_0=x_0, x_1=x_1)
# The model predicts the logits for x_1 given x_t and t
logits = model(x=path_sample.x_t, t=path_sample.t)
# discrete flow matching generalized KL loss or Cross Entropy loss
if loss_type == 'KL':
loss = loss_fn(logits=logits, x_1=x_1, x_t=path_sample.x_t, t=path_sample.t)
elif loss_type == 'CE':
loss = loss_fn(einops.rearrange(logits, 'b n d -> (b n) d'),
einops.rearrange(x_1, 'b n -> (b n)'))
# optimizer step
optim.zero_grad()
loss.backward()
optim.step()
# loss logging
losses.append(loss.item())
pbar.set_description(f'{prefix}, Loss = {loss.item():2.3f}')
# checkpoint
savepath = os.path.join(SAVE_PATH, f'{model_name}.pth')
checkpoint = {'model': model.state_dict(),
'loss': np.array(losses)}
torch.save(checkpoint, savepath)
return model, losses
3. ELBO Estimates
The generalized KL divergence is also used to compute ELBO estimates:
\[\log{p_1(x_1)} \geq -\sum_i \textbf{E}_{t, (X_0, X_1), X_t}\frac{\dot{\kappa_t}}{1-\kappa_t}\left[(\delta_{x_1}(x_t^i) - 1)\log{p_{1 \mid t}(x_1^i \mid x_t)} + \delta_{x_1}(x_t^i) - p_{1 \mid t}(x_1^i \mid x_t) \right]\]# elbo estimate given any x_1 in the domain but not necessarity in the data distribution
def elbo_estimate(x_1, model, path, vocab_size, source_distribution, n_discretization=1024, n_samples=25):
model.eval()
assert x_1.device == next(model.parameters()).device
device = x_1.device
dim = x_1.shape[1]
generalized_kl_fn = MixturePathGeneralizedKL(path = path, reduction ='none')
discretization = torch.linspace(0, 1, n_discretization + 1, device=device)[:-1].view(-1, 1).repeat(1, x_1.shape[0])
elbo = torch.zeros(size=(x_1.shape[0], ), device=device)
with torch.no_grad():
for _ in tqdm(range(n_samples)):
# Lower variance estimator for time discretization
discretization = discretization + torch.rand(size=(1, x_1.shape[0]), device=device)
discretization = discretization % 1
discretization = discretization * (1.0 - 1e-4)
for t in discretization:
# sample X_t ~ p_t(\cdot| x_1)
if source_distribution == 'uniform':
x_0 = torch.randint(size=x_1.shape, high=vocab_size, device=device)
elif source_distribution == 'mask':
x_0 = (torch.zeros(size=x_1.shape, device=device) + vocab_size).long()
x_t = path.sample(t=t, x_0=x_0, x_1=x_1).x_t
logits = model(x_t, t)
# compute ELBO
elbo -= generalized_kl_fn(logits=logits, x_1=x_1, x_t=x_t, t=t).sum(dim=1)
elbo /= n_discretization * n_samples
# Remember that log_q(x_1) >= ELBO(x_1)
probability_lower_bound = torch.exp(elbo)
log_prob_lower_bound_per_dim = elbo / dim
return {'elbo': probability_lower_bound,
'logp_per_dim': log_prob_lower_bound_per_dim}
2D Case
Here, we generate a 2D checkerboard data as \(x_1\) and train discrete flow matching model to replicate this discrete distributions.
The model is a simple MLP predicting the logits for each position.
def inf_train_gen_2d(n_grid_points: int = 128, batch_size: int = 200, device: str = "cpu") -> Tensor:
assert n_grid_points % 4 == 0, "number of grid points has to be divisible by 4"
n_grid_points = n_grid_points // 4
x1 = torch.randint(low=0, high=n_grid_points * 4, size=(batch_size,), device=device)
samples_x2 = torch.randint(low=0, high=n_grid_points, size=(batch_size,), device=device)
x2 = (
samples_x2
+ 2 * n_grid_points
- torch.randint(low=0, high=2, size=(batch_size,), device=device) * 2 * n_grid_points
+ (torch.floor(x1 / n_grid_points) % 2) * n_grid_points
)
x_end = 1.0 * torch.cat([x1[:, None], x2[:, None]], dim=1)
return x_end.long()
# Activation class
class Swish(torch.nn.Module):
def __init__(self):
super().__init__()
def forward(self, x: Tensor) -> Tensor:
return torch.sigmoid(x) * x
# Model class
class MLP(torch.nn.Module):
def __init__(
self, input_dim: int = 128, time_dim: int = 1, hidden_dim=128, length=2):
super().__init__()
self.input_dim = input_dim
self.time_dim = time_dim
self.hidden_dim = hidden_dim
self.time_embedding = torch.nn.Linear(1, time_dim)
self.token_embedding = torch.nn.Embedding(self.input_dim, hidden_dim)
self.main = torch.nn.Sequential(
Swish(),
torch.nn.Linear(hidden_dim * length + time_dim, hidden_dim),
Swish(),
torch.nn.Linear(hidden_dim, hidden_dim),
Swish(),
torch.nn.Linear(hidden_dim, hidden_dim),
Swish(),
torch.nn.Linear(hidden_dim, self.input_dim * length),
)
def forward(self, x, t):
t = self.time_embedding(t.unsqueeze(-1))
x = self.token_embedding(x)
B, N, d = x.shape
x = x.reshape(B, N * d)
h = torch.cat([x, t], dim=1)
h = self.main(h)
h = h.reshape(B, N, self.input_dim)
return h
class WrappedModel(ModelWrapper):
def forward(self, x: torch.Tensor, t: torch.Tensor, **extras):
return torch.softmax(self.model(x, t), dim=-1)
# hyperparams
hidden_dim = 128
vocab_size = 128
batch_size = 4096
iterations = 30000
# scheduler definition
scheduler = PolynomialScheduler(2.0)
path = MixtureDiscreteProbPath(scheduler=scheduler)
# do a sweep for
# 1. source = ['uniform', 'mask']
# 2. loss = ['KL', 'CE']
# {model, losses, samples}
# samples are dict of different type
rlt_dct = dict()
for source_distribution in ['uniform', 'mask']:
rlt_dct[source_distribution] = dict()
for loss_type in ['KL', 'CE']:
rlt_dct[source_distribution][loss_type] = dict()
input_dim = vocab_size + int(source_distribution == 'mask')
model = MLP(input_dim=input_dim, time_dim=1, hidden_dim=hidden_dim).to(device)
model, losses = train_discrete_flow_matching_model(model, path, inf_train_gen_2d,
loss_type=loss_type,
source_distribution=source_distribution,
model_prefix='twodim',
vocab_size=vocab_size,
batch_size=batch_size,
lr=0.001,
iterations=iterations,
epsilon=1e-4,
device=device)
rlt_dct[source_distribution][loss_type]['model'] = copy.deepcopy(model)
rlt_dct[source_distribution][loss_type]['losses'] = copy.deepcopy(losses)
# training a larger scoring model using the same scheduler:
sc_hidden_dim = 256
sc_iterations = 100000
scoring_model = dict()
for sc_source_distribution in ['uniform', 'mask']:
sc_input_dim = vocab_size + int(sc_source_distribution == 'mask')
sc_model = MLP(input_dim=sc_input_dim, time_dim=1, hidden_dim=sc_hidden_dim).to(device)
sc_model, _ = train_discrete_flow_matching_model(model, path, inf_train_gen_2d,
loss_type='KL',
source_distribution=sc_source_distribution,
model_prefix='score',
vocab_size=vocab_size,
batch_size=batch_size,
lr=0.001,
iterations=sc_iterations,
epsilon=1e-4,
device=device)
scoring_model[sc_source_distribution] = copy.deepcopy(sc_model)
# sampling function
def sample_discrete_flow_matching_model(model, path, vocab_size,
source_distribution='uniform', solver_type='Euler', dim=2, n_samples=1000000, nfe=512, n_plots=8):
assert source_distribution in ['uniform', 'mask']
assert solver_type in ['Euler', 'Heun', 'SimpleEuler', 'SimpleHeun', 'SimpleEulerStochastic', 'SimpleHeunStochastic']
print(f'Sampling with {solver_type} solver')
# infer device
device = next(model.parameters()).device
# model wrapper
model.eval()
wrapped_model = WrappedModel(model)
if solver_type.startswith('Simple'):
solver = SimpleSolver(model=wrapped_model,
path=path,
vocabulary_size=vocab_size + int(source_distribution == 'mask'),
solver_type='Euler' if 'Euler' in solver_type else 'Heun',
stochastic='Stochastic' in solver_type,
source_distribution=source_distribution)
else:
solver = MixtureDiscreteSolver(model=wrapped_model,
path=path,
vocabulary_size=vocab_size + int(source_distribution == 'mask'),
solver_type=solver_type)
step_size = 1.0 / nfe
if source_distribution == 'uniform':
x_0 = torch.randint(0, vocab_size, (n_samples, dim), device=device)
elif source_distribution == 'mask':
x_0 = (torch.zeros((n_samples, dim), device=device) + vocab_size).long()
linspace_to_plot = torch.linspace(0, 1 - 1e-4, n_plots)
sol = solver.sample(x_init=x_0,
step_size=step_size,
verbose=False,
return_intermediates=True,
time_grid=linspace_to_plot)
return sol.cpu().numpy()
def plot_2d_sol(sol, title=None):
n_plots = sol.shape[0]
linspace_to_plot = torch.linspace(0, 1 - 1e-4, n_plots)
fig, axs = plt.subplots(1, n_plots, figsize = (20, 20))
if source_distribution == 'mask':
mask_tensor = torch.tensor([vocab_size, vocab_size]).unsqueeze(0)
for idx, step in enumerate(linspace_to_plot):
sol_step = sol[idx, ...]
if source_distribution == 'mask':
sol_step = sol_step[torch.ne(torch.from_numpy(sol_step), mask_tensor).all(dim=1), ...]
H = axs[idx].hist2d(sol_step[:, 0], sol_step[:, 1], bins=vocab_size)
cmin = 0.0
cmax = torch.quantile(torch.from_numpy(H[0]), 0.95).item()
norm = cm.colors.Normalize(vmax=cmax, vmin=cmin)
_ = axs[idx].hist2d(sol_step[:, 0], sol_step[:, 1], bins=vocab_size, norm=norm)
axs[idx].set_aspect('equal')
axs[idx].axis('off')
axs[idx].set_title(f't= {linspace_to_plot[idx].item():.2f}')
plt.tight_layout()
if title is not None: axs[idx].set_title(f'{title} t= {linspace_to_plot[idx].item():.2f}')
return fig
for source_distribution in ['uniform', 'mask']:
for loss_type in ['KL', 'CE']:
model = rlt_dct[source_distribution][loss_type]['model']
for solver_type in ['Euler', 'Heun', 'SimpleEuler', 'SimpleHeun', 'SimpleEulerStochastic', 'SimpleHeunStochastic']:
rlt_dct[source_distribution][loss_type][solver_type] = dict()
sol = sample_discrete_flow_matching_model(model, path, vocab_size,
source_distribution=source_distribution,
solver_type=solver_type,
dim=2)
rlt_dct[source_distribution][loss_type][solver_type]['sample'] = sol[-1]
# randomly generate plots
if torch.rand(1)[0].item() < 0.1: fig = plot_2d_sol(sol, title=f'{source_distribution}, {loss_type}, {solver_type}\n')

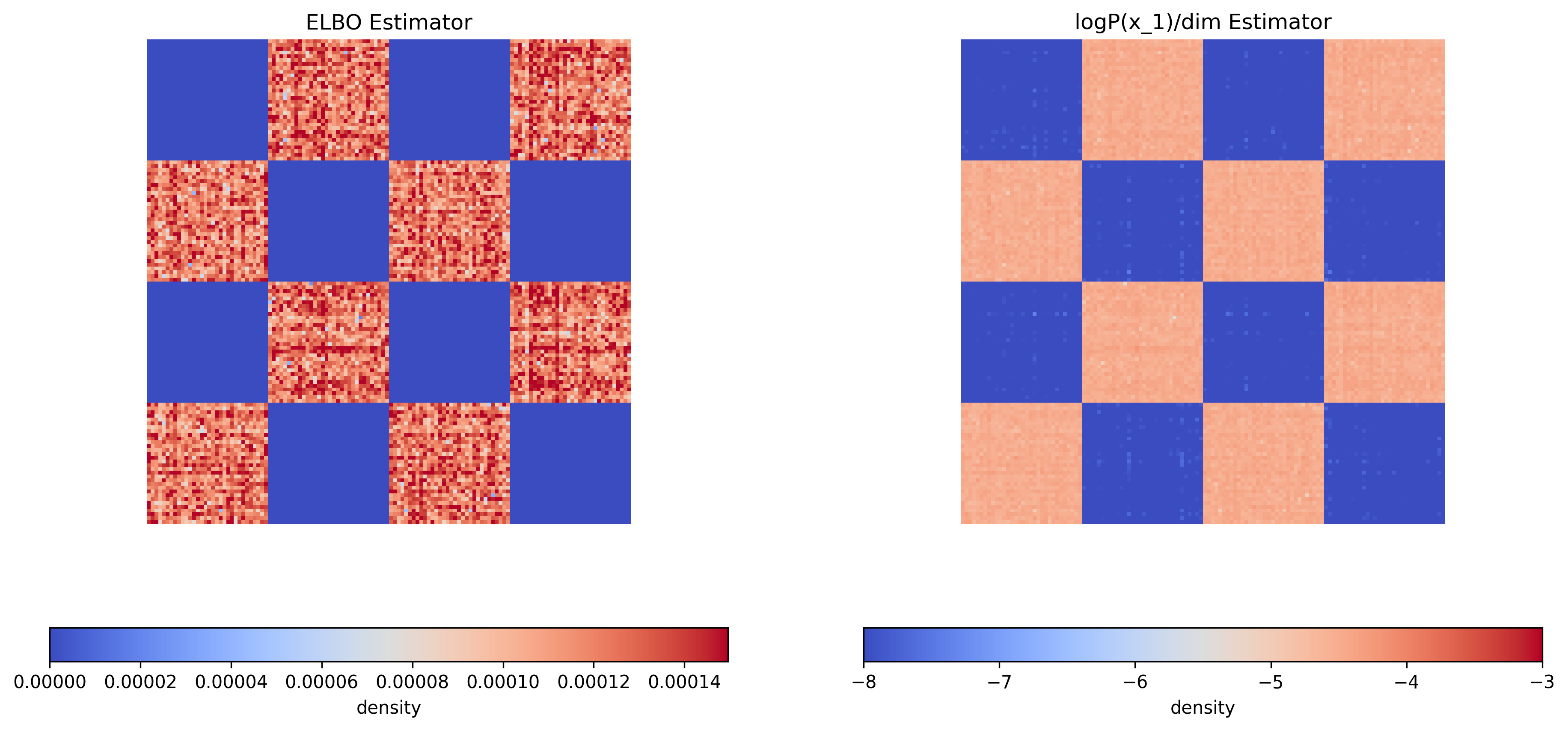
def plot_2d_elbo(elbo_dct):
probability_lower_bound = elbo_dct['elbo']
log_prob_lower_bound_per_dim = elbo_dct['logp_per_dim']
fig, axes = plt.subplots(1, 2, figsize=(15, 7), dpi=300)
cmin = 0.0
cmax = probability_lower_bound.max().item() / 1.5
norm = cm.colors.Normalize(vmax=cmax, vmin=cmin)
axes[0].imshow(probability_lower_bound.reshape(vocab_size, vocab_size).cpu(), origin='lower', cmap='coolwarm', norm=norm)
axes[0].axis('off')
axes[0].set_title('ELBO Estimator')
plt.colorbar(cm.ScalarMappable(norm=norm, cmap='coolwarm'), ax=axes[0], orientation='horizontal', label='density')
cmin = -8.0
cmax = -3.0
norm = cm.colors.Normalize(vmax=cmax, vmin=cmin)
axes[1].imshow(log_prob_lower_bound_per_dim.reshape(vocab_size, vocab_size).cpu(), origin='lower', cmap='coolwarm', norm=norm)
axes[1].axis('off')
axes[1].set_title('logP(x_1)/dim Estimator')
plt.colorbar(cm.ScalarMappable(norm=norm, cmap='coolwarm'), ax=axes[1], orientation='horizontal', label='density')
return fig
# Grid of vocab_size X vocab_size
grid = torch.meshgrid(torch.arange(0, vocab_size, device=device),
torch.arange(0, vocab_size, device=device),
indexing='ij')
x_1 = torch.stack([grid[0].reshape(-1), grid[1].reshape(-1)], dim=1)
# using the last model, (mask, CE)
elbo_dct = elbo_estimate(x_1, model, path, vocab_size, source_distribution)
fig = plot_2d_elbo(elbo_dct)
# show and plot the elbo and logp/dim
for source_distribution in ['uniform', 'mask']:
for loss_type in ['KL', 'CE']:
print(f'\n----- {source_distribution}, {loss_type} -----')
model = rlt_dct[source_distribution][loss_type]['model']
for solver_type in ['Euler', 'Heun', 'SimpleEuler', 'SimpleHeun', 'SimpleEulerStochastic', 'SimpleHeunStochastic']:
x_1 = torch.from_numpy(rlt_dct[source_distribution][loss_type][solver_type]['sample']).to(device)
elbo_dct = elbo_estimate(x_1, model, path, vocab_size, source_distribution)
rlt_dct[source_distribution][loss_type][solver_type].update(elbo_dct)
elbo_mean = elbo_dct['elbo'].mean().item()
log_p_mean = elbo_dct['logp_per_dim'].mean().item()
print(f'{solver_type}, ELBO = {elbo_mean:.8f}, LogP/dim = {log_p_mean:.5f}')
print(f'\n-----')
Uniform
| Method | ELBO (KL / CE) | LogP/dim (KL / CE) |
|---|---|---|
| Euler | 0.00001383 / 0.00001103 | -5.62259 / -5.81091 |
| Heun | 0.00001418 / 0.00001150 | -5.60660 / -5.77359 |
| SimpleEuler | 0.00001381 / 0.00001101 | -5.62421 / -5.81599 |
| SimpleHeun | 0.00001383 / 0.00001107 | -5.62253 / -5.80796 |
| SimpleEulerStochastic | 0.00001374 / 0.00001094 | -5.63223 / -5.82770 |
| SimpleHeunStochastic | 0.00001376 / 0.00001101 | -5.63070 / -5.81804 |
Mask
| Method | ELBO (KL / CE) | LogP/dim (KL / CE) |
|---|---|---|
| Euler | 0.00012449 / 0.00012359 | -4.51112 / -4.51102 |
| Heun | 0.00012453 / 0.00012368 | -4.50965 / -4.50959 |
| SimpleEuler | 0.00012445 / 0.00012361 | -4.51148 / -4.51128 |
| SimpleHeun | 0.00012451 / 0.00012360 | -4.51088 / -4.51113 |
| SimpleEulerStochastic | 0.00012452 / 0.00012361 | -4.51197 / -4.51254 |
| SimpleHeunStochastic | 0.00012451 / 0.00012360 | -4.51180 / -4.51192 |
# Using the scoring model:
print('Using the scoring model: ')
for source_distribution in ['uniform', 'mask']:
model = scoring_model[source_distribution]
for loss_type in ['KL', 'CE']:
print(f'\n----- {source_distribution}, {loss_type} -----')
for solver_type in ['Euler', 'Heun', 'SimpleEuler', 'SimpleHeun', 'SimpleEulerStochastic', 'SimpleHeunStochastic']:
x_1 = torch.from_numpy(rlt_dct[source_distribution][loss_type][solver_type]['sample']).to(device)
elbo_dct = elbo_estimate(x_1, model, path, vocab_size, source_distribution)
rlt_dct[source_distribution][loss_type][solver_type].update(elbo_dct)
elbo_mean = elbo_dct['elbo'].mean().item()
log_p_mean = elbo_dct['logp_per_dim'].mean().item()
print(f'{solver_type}, ELBO = {elbo_mean:.8f}, LogP/dim = {log_p_mean:.5f}')
print(f'\n-----')
Uniform
| Method | ELBO (KL / CE) | LogP/dim (KL / CE) |
|---|---|---|
| Euler | 0.00001458 / 0.00001428 | -5.59203 / -5.74789 |
| Heun | 0.00001462 / 0.00001437 | -5.58809 / -5.70745 |
| SimpleEuler | 0.00001458 / 0.00001426 | -5.59285 / -5.75720 |
| SimpleHeun | 0.00001457 / 0.00001429 | -5.59236 / -5.74419 |
| SimpleEulerStochastic | 0.00001456 / 0.00001422 | -5.59908 / -5.77931 |
| SimpleHeunStochastic | 0.00001457 / 0.00001426 | -5.59803 / -5.76159 |
Mask
| Method | ELBO (KL / CE) | LogP/dim (KL / CE) |
|---|---|---|
| Euler | 0.00012271 / 0.00012283 | -4.51789 / -4.51597 |
| Heun | 0.00012271 / 0.00012290 | -4.51583 / -4.51402 |
| SimpleEuler | 0.00012268 / 0.00012283 | -4.51828 / -4.51631 |
| SimpleHeun | 0.00012272 / 0.00012287 | -4.51744 / -4.51593 |
| SimpleEulerStochastic | 0.00012270 / 0.00012280 | -4.51952 / -4.51832 |
| SimpleHeunStochastic | 0.00012269 / 0.00012284 | -4.51913 / -4.51717 |
Sequence
Building on the previous source type, training loss and ssampling, we now stick to: [uniform-KL, mask-CE] + [Heun] for training a sequence generation model on 1hxe.a2m, which is a MSA from Serine Protease (PDB: 1HXE).
We used fixed length including gaps in the MSA, this enables easy data loading. However, one can train without fixed length data by grouping same-length data in a batch as \(x_1\) and sample noised version of \(x_t\). The sequence length varies from batch to batch, so does the compute (CPU/GPU/Mem). If there is one length being under-represented, one can sample more time point to compensate and get batch of the same size. This might need some massage in the dataloading and preprocessing time, which we don’t do here.
The model backbone is a Discrete Diffusion Transformer (DDiT) module.
# load and process msafile
RESTYPES = ['A', 'R', 'N', 'D', 'C', 'Q', 'E', 'G', 'H', 'I', 'L', 'K', 'M', 'F', 'P', 'S', 'T', 'W', 'Y', 'V']
RESTYPES_WITH_X_GAP = RESTYPES + ['X', '-']
RESTYPE_TO_IDX = {res: i for i, res in enumerate(RESTYPES_WITH_X_GAP)}
def msa_to_torch(msafile):
assert os.path.isfile(msafile)
with open(msafile, 'r') as f: lines = f.readlines()
if msafile.endswith('.a3m'):
seqs = [''.join([a for a in line if a.isupper() or a == '-']) for line in lines if (not line.startswith('#')) and (not line.startswith('>'))]
elif msafile.endswith('.a2m'):
seqs, tmp = [], []
for line in lines:
if line.startswith('>'):
if len(tmp) != 0: seqs.append(''.join(tmp))
tmp = []
else:
tmp.append(line.strip().upper().replace('.', '-'))
nseq, seqlen = len(seqs), len(seqs[0])
data = torch.zeros((nseq, seqlen), dtype=int)
for i, seq in tqdm(enumerate(seqs)):
for j, a in enumerate(seq): data[i, j] = RESTYPE_TO_IDX[a] if a in RESTYPE_TO_IDX else 20
return data
def inf_seq_train_gen(data: Tensor, batch_size: int = 200) -> Tensor:
nseq = data.shape[0]
device = data.device
assert batch_size <= nseq
idx = torch.randint(0, nseq, (batch_size, ), device=device)
return data[idx]
## Model
# # model definition
import math
from typing import Optional, Tuple
import torch
from torch import nn, Tensor
import torch.nn.functional as F
from einops import rearrange, repeat
from omegaconf import OmegaConf
from omegaconf.dictconfig import DictConfig
class Rotary(torch.nn.Module):
"""
From: https://github.com/louaaron/Score-Entropy-Discrete-Diffusion
"""
def __init__(self, dim: int, base: int = 10_000):
super().__init__()
inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float() / dim))
self.register_buffer("inv_freq", inv_freq)
self.seq_len_cached = None
self.cos_cached = None
self.sin_cached = None
def forward(self, x: Tensor, seq_dim: int = 1) -> Tuple[Tensor, Tensor]:
seq_len = x.shape[seq_dim]
if seq_len != self.seq_len_cached:
self.seq_len_cached = seq_len
t = torch.arange(x.shape[seq_dim], device=x.device).type_as(self.inv_freq)
freqs = torch.einsum("i,j->ij", t, self.inv_freq.clone())
emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
# dims are: batch, seq_len, qkv, head, dim
self.cos_cached = emb.cos()[None, :, None, None, :].repeat(1, 1, 3, 1, 1)
self.sin_cached = emb.sin()[None, :, None, None, :].repeat(1, 1, 3, 1, 1)
# This makes the transformation on v an identity.
self.cos_cached[:, :, 2, :, :].fill_(1.0)
self.sin_cached[:, :, 2, :, :].fill_(0.0)
return self.cos_cached, self.sin_cached
def rotate_half(x: Tensor) -> Tensor:
x1, x2 = x[..., : x.shape[-1] // 2], x[..., x.shape[-1] // 2 :]
return torch.cat((-x2, x1), dim=-1)
def apply_rotary_emb_torch(x, cos, sin, interleaved=False):
"""
From: https://github.com/Dao-AILab/flash-attention/blob/main/flash_attn/layers/rotary.py#L20
"""
cos = cos[0, :, 0, 0, : cos.shape[-1] // 2]
sin = sin[0, :, 0, 0, : sin.shape[-1] // 2]
ro_dim = cos.shape[-1] * 2
assert ro_dim <= x.shape[-1]
cos = repeat(
cos, "... d -> ... 1 (2 d)" if not interleaved else "... d -> ... 1 (d 2)"
)
sin = repeat(
sin, "... d -> ... 1 (2 d)" if not interleaved else "... d -> ... 1 (d 2)"
)
return x[..., :ro_dim] * cos + rotate_half(x[..., :ro_dim]) * sin
def bias_dropout_add_scale(
x: Tensor, scale: Tensor, residual: Optional[Tensor], prob: float, training: bool
) -> Tensor:
return residual + scale * F.dropout(x, p=prob, training=training)
def modulate(x: Tensor, shift: Tensor, scale: Tensor) -> Tensor:
return x * (1 + scale) + shift
class LayerNorm(nn.Module):
def __init__(self, dim: int):
super().__init__()
self.weight = nn.Parameter(torch.ones([dim]))
self.dim = dim
def forward(self, x: Tensor) -> Tensor:
with torch.amp.autocast("cuda", enabled=False):
x = F.layer_norm(x.float(), [self.dim])
return x * self.weight[None, None, :]
class TimestepEmbedder(nn.Module):
"""
Embeds scalar timesteps into vector representations.
"""
def __init__(self, hidden_size: int, frequency_embedding_size: int = 256):
super().__init__()
self.mlp = nn.Sequential(
nn.Linear(frequency_embedding_size, hidden_size, bias=True),
nn.SiLU(),
nn.Linear(hidden_size, hidden_size, bias=True),
)
self.frequency_embedding_size = frequency_embedding_size
@staticmethod
def timestep_embedding(time: Tensor, dim: int, max_period: int = 10000) -> Tensor:
"""
Create sinusoidal timestep embeddings.
:param t: a 1-D Tensor of N indices, one per batch element.
These may be fractional.
:param dim: the dimension of the output.
:param max_period: controls the minimum frequency of the embeddings.
:return: an (N, D) Tensor of positional embeddings.
"""
half = dim // 2
freqs = torch.exp(
-math.log(max_period)
* torch.arange(start=0, end=half, dtype=torch.float32)
/ half
).to(device=time.device)
args = time[:, None].float() * freqs[None]
embedding = torch.cat([torch.cos(args), torch.sin(args)], dim=-1)
if dim % 2:
embedding = torch.cat(
[embedding, torch.zeros_like(embedding[:, :1])], dim=-1
)
return embedding
def forward(self, time: Tensor) -> Tensor:
t_freq = self.timestep_embedding(time=time, dim=self.frequency_embedding_size)
t_emb = self.mlp(t_freq)
return t_emb
class DDiTBlock(nn.Module):
def __init__(
self,
dim: int,
n_heads: int,
cond_dim: int,
mlp_ratio: int = 4,
dropout: float = 0.1,
):
super().__init__()
assert dim % n_heads == 0, "dim must be devisable by n_heads"
self.n_heads = n_heads
self.dim = dim
self.dropout = dropout
self.head_dim = self.dim // self.n_heads
self.norm1 = LayerNorm(dim=dim)
self.qw = nn.Linear(dim, dim, bias=False)
self.kw = nn.Linear(dim, dim, bias=False)
self.vw = nn.Linear(dim, dim, bias=False)
self.attn_out = nn.Linear(dim, dim, bias=False)
self.dropout1 = nn.Dropout(dropout)
self.norm2 = LayerNorm(dim=dim)
self.mlp = nn.Sequential(
nn.Linear(dim, mlp_ratio * dim, bias=True),
nn.GELU(approximate="tanh"),
nn.Linear(mlp_ratio * dim, dim, bias=True),
)
self.adaLN_modulation = nn.Linear(cond_dim, 6 * dim, bias=True)
self.adaLN_modulation.weight.data.zero_()
self.adaLN_modulation.bias.data.zero_()
def forward(self, x: Tensor, rotary_cos_sin: Tensor, c: Tensor) -> Tensor:
batch_size, seq_len = x.shape[0], x.shape[1]
(
shift_msa,
scale_msa,
gate_msa,
shift_mlp,
scale_mlp,
gate_mlp,
) = self.adaLN_modulation(c)[:, None].chunk(6, dim=2)
x_skip = x
x = modulate(x=self.norm1(x), shift=shift_msa, scale=scale_msa)
q = self.qw(x)
k = self.kw(x)
v = self.vw(x)
q, k, v = (
item.view(batch_size, seq_len, self.n_heads, self.head_dim)
for item in (q, k, v)
)
with torch.amp.autocast("cuda", enabled=False):
cos, sin = rotary_cos_sin
original_dtype = q.dtype
q = apply_rotary_emb_torch(
x=q.float(), cos=cos.float(), sin=sin.float()
).to(original_dtype)
k = apply_rotary_emb_torch(
x=k.float(), cos=cos.float(), sin=sin.float()
).to(original_dtype)
q, k, v = (item.transpose(1, 2) for item in (q, k, v))
x = F.scaled_dot_product_attention(query=q, key=k, value=v)
x = rearrange(x, "b h s d -> b s (h d)", b=batch_size)
x = bias_dropout_add_scale(
x=self.attn_out(x),
scale=gate_msa,
residual=x_skip,
prob=self.dropout,
training=self.training,
)
x = bias_dropout_add_scale(
x=self.mlp(modulate(x=self.norm2(x), shift=shift_mlp, scale=scale_mlp)),
scale=gate_mlp,
residual=x,
prob=self.dropout,
training=self.training,
)
return x
class DDitFinalLayer(nn.Module):
def __init__(self, hidden_size: int, out_channels: int, cond_dim: int):
super().__init__()
self.norm_final = LayerNorm(hidden_size)
self.linear = nn.Linear(hidden_size, out_channels)
self.linear.weight.data.zero_()
self.linear.bias.data.zero_()
self.adaLN_modulation = nn.Linear(cond_dim, 2 * hidden_size, bias=True)
self.adaLN_modulation.weight.data.zero_()
self.adaLN_modulation.bias.data.zero_()
def forward(self, x: Tensor, c: Tensor) -> Tensor:
shift, scale = self.adaLN_modulation(c)[:, None].chunk(2, dim=2)
x = modulate(x=self.norm_final(x), shift=shift, scale=scale)
x = self.linear(x)
return x
class Transformer(nn.Module):
def __init__(self, vocab_size: int, masked: bool, config: DictConfig):
super().__init__()
if isinstance(config, dict):
config = OmegaConf.create(config)
self.config = config
self.vocab_size = vocab_size
add_token = 1 if masked else 0
self.vocab_embed = nn.Embedding(self.vocab_size + add_token, config.hidden_size)
self.time_embedding = TimestepEmbedder(hidden_size=config.cond_dim)
self.rotary_emb = Rotary(dim=config.hidden_size // config.n_heads)
self.blocks = nn.ModuleList(
[
DDiTBlock(
dim=config.hidden_size,
n_heads=config.n_heads,
cond_dim=config.cond_dim,
dropout=config.dropout,
)
for _ in range(config.n_blocks)
]
)
self.output_layer = DDitFinalLayer(
hidden_size=config.hidden_size,
out_channels=vocab_size + add_token,
cond_dim=config.cond_dim,
)
def forward(self, x_t: Tensor, time: Tensor) -> Tensor:
x = self.vocab_embed(x_t)
c = F.silu(self.time_embedding(time=time))
rotary_cos_sin = self.rotary_emb(x=x)
with torch.amp.autocast("cuda", dtype=torch.bfloat16):
for i in range(len(self.blocks)):
x = self.blocks[i](x=x, rotary_cos_sin=rotary_cos_sin, c=c)
x = self.output_layer(x=x, c=c)
return x
Training
msafile = '1hxe.a2m'
msa = msa_to_torch(msafile)
vocab_size = 22
train = False
scheduler = PolynomialScheduler(2.0)
path = MixtureDiscreteProbPath(scheduler=scheduler)
lr = 0.0001
batch_size = 2048
iterations = 20000
embed_size = 64
n_blocks = 4
epsilon = 1e-3
seq_models = []
source_loss_combo = [('uniform', 'KL'),
('mask', 'CE')]
for (source_distribution, loss_type) in source_loss_combo:
# training arguments
if source_distribution == "uniform":
added_token = 0
elif source_distribution == "mask":
mask_token = vocab_size # tokens starting from zero
added_token = 1
else:
raise NotImplementedError
# additional mask token
vocab_size += added_token
# probability denoiser model init
# Model initialization
cfg = OmegaConf.load('config.yaml')
cfg.model.n_blocks = n_blocks
cfg.model.dropout = 0.3
probability_denoiser = Transformer(config=cfg.model, vocab_size=vocab_size, masked=False).to(device)
print('Number of parameters =', sum(param.numel() for param in probability_denoiser.parameters()))
# init optimizer
optim = torch.optim.Adam(probability_denoiser.parameters(), lr=lr)
loss_fn = MixturePathGeneralizedKL(path=path) if loss_type == 'KL' else torch.nn.CrossEntropyLoss()
# train
if train:
start_time = time.time()
steps = 0
losses = []
pbar = tqdm(range(iterations + 1))
for i in pbar:
# sample data (user's responsibility): in this case, (X_0,X_1) ~ pi(X_0,X_1)
x_1 = inf_seq_train_gen(msa, batch_size=batch_size).to(device) # sample data
if source_distribution == "uniform":
x_0 = torch.randint_like(x_1, high=vocab_size)
elif source_distribution == "mask":
x_0 = torch.zeros_like(x_1) + mask_token
else:
raise NotImplementedError
# sample time (user's responsibility)
t = torch.rand(x_1.shape[0]).to(device) * (1 - epsilon)
# sample probability path
# mixture of discrete probability path for each token
path_sample = path.sample(t=t, x_0=x_0, x_1=x_1)
# discrete flow matching generalized KL loss
logits = probability_denoiser(path_sample.x_t, path_sample.t)
if loss_type == 'KL':
loss = loss_fn(logits=logits, x_1=x_1, x_t=path_sample.x_t, t=path_sample.t)
elif loss_type == 'CE':
loss = loss_fn(einops.rearrange(logits, 'b n d -> (b n) d'),
einops.rearrange(x_1, 'b n -> (b n)'))# This should be consistent with the following:
# logit_to_velocity(pred_x_1, x_t, t) - logit_to_velocity(x_1, x_t, t)
# optimizer step
optim.zero_grad()
loss.backward() # backward
optim.step() # update
pbar.set_description(f'loss = {loss.item():.3f}')
torch.save(probability_denoiser.state_dict(), f'seq_{source_distribution}_{loss_type}.pth')
else:
probability_denoiser.load_state_dict(torch.load(f'seq_{source_distribution}_{loss_type}.pth', weights_only=True))
seq_models.append(copy.deepcopy(probability_denoiser))
Sampling
%%time
vocab_size = 22
seq = ''.join([RESTYPES_WITH_X_GAP[a] for a in msa[0]])
seqs = []
sols = []
for i, (source_distribution, loss_type) in enumerate(source_loss_combo):
model = seq_models[i]
sol = sample_discrete_flow_matching_model(model, path, vocab_size,
source_distribution=source_distribution,
solver_type='Heun',
dim=msa.shape[1],
n_samples=256, nfe=1024, n_plots=8)
sols.append(sol[-1])
seqs.append([''.join([RESTYPES_WITH_X_GAP[a] for a in s]) for s in sol[-1]])
print()
print(source_distribution, loss_type)
print('Original')
print(seq)
print('Samples')
for j in range(5): print(seqs[i][j])
print()
Sampling with Heun solver
uniform KL
Original
IVEGSDAEIGMSPWQVMLFRKSPQELLCGASLISDRWVLTAAHCLLYPPWDKNFTENDLLVRIGKHSRTRYERNIEKISMLEKIYIHPRYNWRENLDRDIALMKLKKPVAFSDYIHPVCLPDRETAASLLQAGYKGRVTGWGNLKETWTANVGKGQPSVLQVVNLPIVERPVCKDSTRIRITDNMFCAGYKPDEGKRGDACEGDSGGPFVMKSPFNNRWYQMGIVSWGEGCDRDGKYGFYTHVFRLKKWIQKVIDQFGE
Samples
IVGGANAPAGSWPWQVSLQING–GHFCGGSLINNEWVLSAAHCFPS——-STSGIQVNLGRQNLQGSNPN-EVFRSVSTIIIHPNYNS-DSNDNDIALLRLSSPVTFNNYISPVCLAASG—STFHNGTDCWVTGFGDIRSD—-VPLPFPNTLQEVQVPVIGNRQCNCNYGGSITGNMICAGL———————————————————————
IVGGSEAELGEWPWQVSLRYNR–SHICGGALVSDKWILSAAHCFEEY—–RDPAEWKVYMGLYSQDSLNK–YKGISVKQIISHPNYNP-ETKDYDIALLQLEEPVLYTNFVQPICLPRSG—HVFPPGTICWITGWGRIQEE——GSSSNALQKAMVPIIDRHFCSRLYPSGIKPGMICAGFI–EGG-VDACQGDSGGPLVCKE-KGSIFFLAGITSWGIGCGLPNKPGVYTRVTELNSWIREKM—–
IVGGSAAEISTYPWQVSLTSGG–RHFCGGSVVAPKIVLTAAHCVVG——-QPSSIRVRVGRTDKATGGG—QIISVSEQWIHPKYND-NTNDGDWALIKLAQPIAYSPAIQTISLATTA—–YAAGTTATVSGWGATTGT——GDYANTLRAVAVPLVSDTECRAAYPGDLTDNMVCAGYL–DGG-RDACQGDSGGPLVAGG——KLVGLVSWGYGCGQAGKPGVYTEVS—————
IVGGEDAPAGSWPWQVSLHTFG—HFCGGSLINNEWVVTAAHCFSR—————LGRHSLEGSNPN-EQSLSVSRVIKHPNYDS-STNDNDICLLQLQSPVTLTNYVRPVCLAASG—SVFANGTNSWVTGWGNTAEG—-VSLPFPANLQEVEVPVLGNRQCKCLYGSTITNNMICAGLL–AGG-KDSCQGDSGGPMVSKN–NSVWIQSGVVSWGYGCALPNYPGVYTRVSEYQSWINSQI—–
IVGGEDAPAGSWPWQVSLHTFG–GHFCGGSLINKEWVLSAAHCFQS——WSTAGWEVYLGRQSLQGNNPN-EQSRTVSKIIIHPNYDS-RTNDNDIALLQLSSPVTFNNYIRPVCLAAFG—SVFNSGTSSWVTGWGNVEEG———PDTLMEVMVPVVGNRQCNCLYGVTITNNMICAGYL–AGG-KDSCQGDSGGPLVSKQ–GSRWVQAGIVSFGIGCAQPNKPGVYARVSRYQTWINSNI—–
Sampling with Heun solver
mask CE
Original
IVEGSDAEIGMSPWQVMLFRKSPQELLCGASLISDRWVLTAAHCLLYPPWDKNFTENDLLVRIGKHSRTRYERNIEKISMLEKIYIHPRYNWRENLDRDIALMKLKKPVAFSDYIHPVCLPDRETAASLLQAGYKGRVTGWGNLKETWTANVGKGQPSVLQVVNLPIVERPVCKDSTRIRITDNMFCAGYKPDEGKRGDACEGDSGGPFVMKSPFNNRWYQMGIVSWGEGCDRDGKYGFYTHVFRLKKWIQKVIDQFGE
Samples
IVGGSEATPGSHPWQAALYISPAEKVFCGGSLIDKCWVATAAHCFKDE——REQYVTVVLGDHHLNRTEGS-EQSLKVEEAIIHPCYNP-SSYDSDIALLKLKHPAKLSKAVSPVCLPEET—QIFSAGSECTISGWGQTEEG—–ADSYSVVLQEAQVPLIDQEQCSKPYGTELDENMMCAGYM–EGG-ADSCQGDSGGPLTCQW–DGRMFLLGITSWGYGCAKPNKPGVYTRVTNFSEWIQSTT—–
VVGGYEAVQSKLPYNVSIQQGQSNSHFCSGALINERWVLTAAHCVMRR—YHLPRNQLEAVLGTHKLTSGGSL-GQTRRVTTIIRHPDGKDVCKYRSNIALIELNPKVNF–KVQPIRISDED—–LTPNTKCIVAGWGITKAG——-GEVLPLNKATVPYVNERACKEYHLEFLGKETLCVGHD–QGL-RGVCDGDAGGGLFCKT-SNDPWKLTGIAVGGQEPCSFTGPSIYIDIRHHLEWLMQNI—–
VAGGNDGRPGAHPWIVALFRNG–THFCGGSLIKGSWVLSAAHCFYNH—-NTDGSDLVAIVGDHQLNRHDGE-EVLVAVSGVIMNQQYNP-NTLQYDIALIKLVQPVSFTEYIQPICLPSPR—VELNENRVCTVTGWGTTQPG—-APPLVSNPLQSVAVPVQATGDCKAAYSHSITDRMLCAGYR–EGN-KDSCQGDSGGPLLCRN–GEQYELHGVVSWGFGCGHPDFYAVYVRTSYLIQWINQTT—–
IVGGADTTINQYPAQVSLLISSGGWHFCGGSIINNRWILTGAHCSHA——-SPNFRRVRVGSSFASEGG—–VHNVERIIVHEGYDW-LTHDNDISVLRLSTALTFSNNIQPAPIAGAN—TTVGENDAAWAAGWGATANG——GGSENALQHVQVPVVNQRQCRRNYANRITNNMICSGWL-GAGG-RDSCQGDSGGPLTHNG——TLVGVCSFGIGCALRRYPGVYARVSSYSSWIDAN——
IIGGRLVTNESRPYQVSLRKEDSKRHSCGGFLISERFALTAAHCNLEP-RSFGQVPALTNVRVGSSFTSSGG—–LHPVRRLIVHPNYDE-QTLDHDIRLLQLDRKVHLNDTVRVVSLPDSP—-DVEDNTLCTTSGWGTTEPDTVKSG-IERPDELRELKLTILNA-ACARQ——-RHLCTGVP–KRE-SGPCAGDSGGPLVCNG——PVHGVASYSRNCG——-FTKIATYVTWLLGQT—–
CPU times: user 49.7 s, sys: 5.29 ms, total: 49.7 s
Wall time: 49.8 s
For serine protease, the first couple of residues are critical for substrate recognition and binding. These residues often form the active site and are highly conserved across different species. In the sample, many of the sequences has similar IVEGS and PWQV motifs from the uniform KL track. The mask CE track also captures these motifs, but with more variability. Uniform source distribution is therefore preferred by many DFM models empirically.

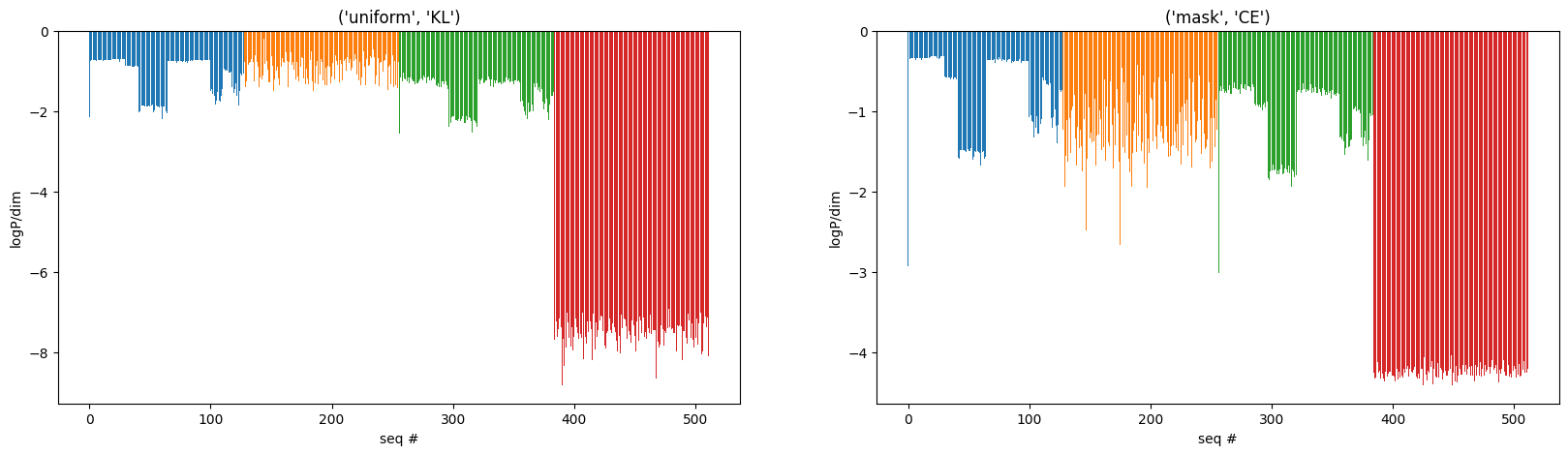
Next, we want to assess the ELBO score for 512 sequences:
128 from the training set, index 0 being the query 1hxe.pdb sequence
128 sampled sequences
128 from the training data, with 10 N-term residue randomly mutated
128 random sequence.
As the following histogram shows, the sampled sequences have the highest ELBO and logP/dim (preferred), and the random sequences being highly unlikely with the most negative ELBO estimates.
When the first 10 residues are mutated (highly preserved regions), the ELBO dropped, suggesting that the ELBO score can be used to gauge the quality of the sequence.
The first spike was from the query, as most of the sequences in the MSA contain gap, a no-gap query sequence then becomes an outlier with high ELBO scores. One proper way to do this is to remove the gaps in the MSA or masked the gap prediction in the loss.
# compute the elbo and logP for original seq, samples and random seqs
# Generalized KL function (will use it to compute the elbo)
generalized_kl_fn = MixturePathGeneralizedKL(path = path, reduction ='none')
elbo_dcts = []
for i, (source_distribution, loss_type) in enumerate(source_loss_combo):
model = seq_models[i]
# first 10 position random mutation
mut = msa[:128].clone()
mut[:, :10] = torch.randint_like(mut[:, :10], high=vocab_size)
x_1 = torch.cat([msa[:128],
torch.from_numpy(sols[i][:128]),
mut,
torch.randint_like(msa[:128], high=vocab_size)]).to(device)
elbo_dcts.append(elbo_estimate(x_1, model, path, vocab_size, source_distribution))
fig, axes = plt.subplots(1, 2, figsize=(20, 5))
c = [-1] + [0] * 127 + [1] * 128 + [2] * 128 + [3] * 128
for i in range(2):
my_cmap = plt.get_cmap('tab10')
# rescale = lambda y: (y - np.min(y)) / (np.max(y) - np.min(y))
axes[i].bar(range(512), elbo_dcts[i]['logp_per_dim'].cpu(), color=my_cmap(c))
axes[i].set_title(source_loss_combo[i])
axes[i].set_xlabel('seq #')
axes[i].set_ylabel('logP/dim')
axes[i]