SE(3) Score-Matching Diffusion Model

apt-get -qq install libsuitesparse-dev
pip install -qq trimesh plotly theseus-ai

# import the required packages
import torch, trimesh

import numpy as np
import matplotlib.pyplot as plt

from torch import nn
from tqdm.auto import tqdm
from trimesh import viewer
from IPython import display
from torch.autograd import grad
from theseus.geometry.so3 import SO3

import plotly.graph_objects as go
from plotly.express.colors import sample_colorscale


# plot the SO(3) distributions
X0 = torch.tensor([0., 0., 1.]) # using the z axis to show the rotations
def plot_rotations(rotmats, x0=X0, labels=None, cmap='jet'):
    '''Plot the rotation matrices contained in a list: rotmats
    colored coded by the order in the list
    '''

    x = np.linspace(0, 1, len(rotmats))
    c = sample_colorscale(cmap, list(x))

    d = []
    for i, rotmat in enumerate(rotmats):
        rotated_x0 = rotmat @ x0
        d.append(go.Scatter3d(name=labels[i] if labels is not None else f'{i}',
                              x=rotated_x0[:, 0],
                              y=rotated_x0[:, 1],
                              z=rotated_x0[:, 2],
                              marker=dict(size=2, opacity=0.75, color=c[i]), mode='markers', ))

    d.append(go.Scatter3d(name='x0',
                          x=x0[0:1],
                          y=x0[1:2],
                          z=x0[2:],
                          marker=dict(size=5, opacity=1.0, color='black'), mode='markers'))

    fig = go.Figure(data=d)
    fig.update_layout(width=800, height=800)
    fig.show()
    return None


# visualize the angle and positions of SE(3) as robot grasps or forks
def create_gripper_marker(color=[0, 0, 255], tube_radius=0.001, sections=6, scale=1.):
    """Create a 3D mesh visualizing a parallel yaw gripper. It consists of four cylinders.

    Args:
        color (list, optional): RGB values of marker. Defaults to [0, 0, 255].
        tube_radius (float, optional): Radius of cylinders. Defaults to 0.001.
        sections (int, optional): Number of sections of each cylinder. Defaults to 6.

    Returns:
        trimesh.Trimesh: A mesh that represents a simple parallel yaw gripper.
    """
    cfl = trimesh.creation.cylinder(
        radius=0.002*scale,
        sections=sections,
        segment=[
            [4.10000000e-02*scale, -7.27595772e-12*scale, 6.59999996e-02*scale],
            [4.10000000e-02*scale, -7.27595772e-12*scale, 1.12169998e-01*scale],
        ],
    )
    cfr = trimesh.creation.cylinder(
        radius=0.002*scale,
        sections=sections,
        segment=[
            [-4.100000e-02*scale, -7.27595772e-12*scale, 6.59999996e-02*scale],
            [-4.100000e-02*scale, -7.27595772e-12*scale, 1.12169998e-01*scale],
        ],
    )
    cb1 = trimesh.creation.cylinder(
        radius=0.002*scale, sections=sections, segment=[[0, 0, 0], [0, 0, 6.59999996e-02*scale]]
    )
    cb2 = trimesh.creation.cylinder(
        radius=0.002*scale,
        sections=sections,
        segment=[[-4.100000e-02*scale, 0, 6.59999996e-02*scale], [4.100000e-02*scale, 0, 6.59999996e-02*scale]],
    )

    tmp = trimesh.util.concatenate([cb1, cb2, cfr, cfl])
    tmp.visual.face_colors = color
    tmp.visual.vertex_colors = color

    return tmp

# Visualize a set of SE(3) elements H (..., 4, 4)
# by creating forks for each fork from the above function
def visualize_grasps(Hs, scale=1., p_cloud=None, energies=None, colors=None, mesh=None, show=True):

    # Set color list
    if colors is None:
        if energies is None:
            color = np.zeros(Hs.shape[0])
        else:
            min_energy = energies.min()
            energies -=min_energy
            color = energies/(np.max(energies)+1e-6)

    # Grips
    grips = []
    for k in range(Hs.shape[0]):
        H = Hs[k,...]

        if colors is None:
            c = color[k]
            c_vis = [0, 0, int(c*254)]
        else:
            c_vis = list(np.array(colors[k,...]))

        grips.append(
            create_gripper_marker(color=c_vis, scale=scale).apply_transform(H)
        )

    # Visualize grips and the object
    if mesh is not None:
        scene = trimesh.Scene([mesh]+ grips)
    elif p_cloud is not None:
        p_cloud_tri = trimesh.points.PointCloud(p_cloud)
        scene = trimesh.Scene([p_cloud_tri]+ grips)
    else:
        scene = trimesh.Scene(grips)

    if show:
        scene.show()
    else:
        return scene

torch.manual_seed(37)
ATOL, RTOL = 1e-5, 1e-5

# Dummy rotations for visualization of a sphere
R_dummy = SO3().exp_map(1.5 * torch.randn(500, 3)).to_matrix()

# v or v_vee is the axis-angle vector representation, in R^3
# v_hat is the lie algebra, in so(3) or skew symmetric matrix
# R is the 3D rotation matrix, in SO(3)

# initialize vector or axis angle representation
v1 = torch.randn(1, 3)
v2 = torch.randn(1, 3)

# rotation matrices from Exp
R1 = SO3().exp_map(v1).to_matrix()
R2 = SO3().exp_map(v2).to_matrix()

# skew symmetric matrix in so(3)
v1_hat = SO3().hat(v1)
v2_hat = SO3().hat(v2)
print('Example of the so3 skew symmetric matrix:')
print(v1_hat)


# check the consistency between vector and rotation
# 1 + 2 cos(theta) = trace(R), where theta is the length of the vector
assert torch.allclose(1. + 2. * torch.cos(v1.norm()),
                      torch.diagonal(R1, dim1=-1, dim2=-2).sum(), atol=ATOL)
assert torch.allclose(1. + 2. * torch.cos(v2.norm()),
                      torch.diagonal(R2, dim1=-1, dim2=-2).sum(), atol=ATOL)


# 1. check the vee operator
v1_vee = SO3().vee(v1_hat)
v2_vee = SO3().vee(v2_hat)
assert torch.allclose(v1, v1_vee, atol=ATOL, rtol=RTOL)
assert torch.allclose(v2, v2_vee, atol=ATOL, rtol=RTOL)

# 2. the lowercase exp is the matrix exponential from so3 to SO3
assert torch.allclose(R1, torch.matrix_exp(v1_hat), atol=ATOL, rtol=RTOL)
assert torch.allclose(R2, torch.matrix_exp(v2_hat), atol=ATOL, rtol=RTOL)

# 3. the exp_map is the uppercase Exp, from R^3 to SO3
#    we used the SO3().exp_map previously but let's check
#    Exp[.] = exp( hat(.) )
assert torch.allclose(R1, torch.matrix_exp(SO3().hat(v1)), atol=ATOL, rtol=RTOL)
assert torch.allclose(R2, torch.matrix_exp(SO3().hat(v2)), atol=ATOL, rtol=RTOL)

# 4. the log_map is the uppercase Log_map from SO(3) to R^3
assert torch.allclose(v1, SO3(tensor=R1).log_map(), atol=ATOL, rtol=RTOL)
assert torch.allclose(v2, SO3(tensor=R2).log_map(), atol=ATOL, rtol=RTOL)

# 5. the log operation: log R = v_hat = theta * (R - R^T) / (2 sin(theta))
assert torch.allclose(v1_hat, v1.norm() * (R1 - R1.transpose(-1, -2)) / 2. / torch.sin(v1.norm()),
                      atol=ATOL, rtol=RTOL)
assert torch.allclose(v2_hat, v2.norm() * (R2 - R2.transpose(-1, -2)) / 2. / torch.sin(v2.norm()),
                      atol=ATOL, rtol=RTOL)

# Outputs: 
# Example of the so3 skew symmetric matrix:
# tensor([[[ 0.0000, -0.5821,  1.2653],
#          [ 0.5821,  0.0000, -0.7207],
#          [-1.2653,  0.7207,  0.0000]]])

# Operation for the SO(3) group

# 1. hat(v1 + v2) = hat(v1) + hat(v2)
#    because v and v_hat are in the same vector space
assert torch.allclose(v1_hat + v2_hat, SO3().hat(v1 + v2), atol=ATOL, rtol=RTOL)


# 2. compose the rotation by right multiplication
R3 = R1 @ R2
assert torch.allclose(R3, torch.einsum('...ij,...jk->...ik', R1, R2), atol=ATOL, rtol=RTOL)



# 3. compose the vector:
#    The rotation composition is not commutative, i.e. R1 @ R2 != R2 @ R1
#    so apparently, Exp_map(v1 + v2) != R1 @ R2.
#    The reason is that the geodesic of Exp_map(v1) is different from geodesic of Exp_map(v2)
#    To get the vector representation from v1 and v2, we will need to
#    - compose the corresponding rotations
#    - transform it back by taking the Log_map
def compose_rotvec(v1, v2):
  R1 = SO3().exp_map(v1).to_matrix()
  R2 = SO3().exp_map(v2).to_matrix()
  R3 = R1 @ R2
  return SO3(tensor=R3).log_map()

v3_a = compose_rotvec(v1, v2)
v3_b = compose_rotvec(v2, v1)

assert not torch.allclose(v3_a, v3_b)
assert torch.allclose(R1 @ R2, SO3().exp_map(v3_a).to_matrix(), atol=ATOL, rtol=RTOL)
assert torch.allclose(R2 @ R1, SO3().exp_map(v3_b).to_matrix(), atol=ATOL, rtol=RTOL)



# 4. Interpolations between two rotations on the SO3 geodesic
#    See: https://en.wikipedia.org/wiki/Slerp
def slerp(R1, R2, weights):
  assert R1.shape[0] == R2.shape[0] == weights.shape[0]
  assert (weights <= 1.0).any() and (weights >= 0.0).any()

  R1_norm = R1 / torch.norm(R1, dim=1, keepdim=True)
  R2_norm = R2 / torch.norm(R2, dim=1, keepdim=True)
  omega = torch.acos((R1_norm * R2_norm).sum(1))
  so = torch.sin(omega)
  res = (torch.sin((1.0 - weights[..., None]) * omega) / so).unsqueeze(1) * R1 + (torch.sin(weights[..., None] * omega) / so).unsqueeze(1) * R2
  return res

assert torch.allclose(slerp(R1, R2, torch.tensor([1.0])), R2, atol=ATOL, rtol=RTOL)
assert torch.allclose(slerp(R1, R2, torch.tensor([0.0])), R1, atol=ATOL, rtol=RTOL)

torch.manual_seed(42)
w = torch.rand(1)
assert torch.allclose(slerp(R1, R2, w), slerp(R2, R1, 1. - w), atol=ATOL, rtol=RTOL)



# 5. "Scale" a rotation by geodesic interpolation
#    Scaling operator can be done with a weighted interpolation between identity and the rotation
#    0 <= scale <= 1
def scale_rotations(R, scale):
  assert len(R.shape) == 3
  assert R.shape[0] == scale.shape[0]
  assert (scale <= 1.0).any() and (scale >= 0.0).any()
  batch = R.shape[0]
  return slerp(torch.eye(3)[None, ...].repeat(batch, 1, 1), R, scale) # just use SLERP

assert torch.allclose(R1, scale_rotations(R1, torch.ones(1)), atol=ATOL, rtol=RTOL)
assert torch.allclose(torch.eye(3)[None, ...], scale_rotations(R1, torch.zeros(1)), atol=ATOL, rtol=RTOL)


# 5. "Scale" a rotation by scaling the angle while fixing the axis
#    Scaling a rotation by 0 = Identity (zero degree)
#    Scaling a rotation by 0.5 = rotate (0.5 * theta) wrt the same axis
#    Scaling a rotation by 1.0 = the same ratation
#    Therefore, again, 0 <= scale <= 1
def scale_rotations_by_angle(R, scale):
  assert len(R.shape) == 3
  assert R.shape[0] == scale.shape[0]
  assert (scale <= 1.0).any() and (scale >= 0.0).any()

  v = SO3(tensor=R).log_map() # convert from R to v
  scaled_v = v * scale[..., None] # scale v, changing the theta while keeping the axis the same
  return SO3().exp_map(scaled_v).to_matrix() # convert it back to the rotation matrix by Exp


# 6. Visualizing scaled rotations and interpolated rotations
n_scale = 1000
scales = torch.linspace(0.0, 1.0, n_scale + 1)

# scaling
rots = [scale_rotations(R1, torch.tensor([scale])) for scale in scales]
plot_rotations([R_dummy] + rots)

# interpolating R1 -> R2
rots = [slerp(R1, R2, torch.tensor([scale])) for scale in scales]
plot_rotations([R_dummy] + rots)

# interpolating R2 -> R1
rots = [slerp(R2, R1, torch.tensor([scale])) for scale in scales]
plot_rotations([R_dummy] + rots)

import requests
from PIL import Image
from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize

url = 'http://images.cocodataset.org/val2017/000000039769.jpg'
image = Image.open(requests.get(url, stream=True).raw)

print('Original Image size = ', ToTensor()(image).shape)

image_size = 128

# a series of transformations
transform = Compose([Resize(image_size),
                     CenterCrop(image_size),
                     ToTensor(), # turn into torch tensor of shape (Height x Width x Channel), divide by 255 in RGB
                     Lambda(lambda t: (t * 2) - 1)])

# inverse transform
reverse_transform = Compose([Lambda(lambda t: (t + 1) / 2),
                             Lambda(lambda t: t.permute(1, 2, 0)), # C x H x W to H x W x C
                             Lambda(lambda t: t * 255.0),
                             Lambda(lambda t: t.numpy().astype(np.uint8)),
                             ToPILImage()])

x_start = transform(image)
print('New Image Size = ', x_start.shape)
x_start = x_start[None, ...]
print('Batched New Image Size = ', x_start.shape)

reverse_transform(x_start[0]) # 2 sleeping cats : )

# Outputs:
# Original Image size =  torch.Size([3, 480, 640])
# New Image Size =  torch.Size([3, 128, 128])
# Batched New Image Size =  torch.Size([1, 3, 128, 128])

# compute the scores
# here because we have access to the single ground truth, we can calculate it directly
# But in the ML problem, we want a NN to learn this
# Note that the function or model inputs are noised_x and time (or std) (we won't have ground truth during sampling)
# and output is an image of vector fields or the score
def compute_score_image(x_noised, x_truth, std, eps=1e-6):
  assert x_noised.shape == x_truth.shape
  assert x_noised.shape[0] == std.shape[0]
  dist = (x_noised - x_truth) # (b, c, w, h)
  return - dist / (std[..., None, None, None] ** 2 + eps)


# following the score back to the sample using Langevin dynamics
# noise_on = False: ODE-like or noise-free
# std_min = std_max: unannealed
def follow_score_image(x_truth, std_min, std_max, T=1500, dt=0.001, noise_on=False, seed=1001):
  assert std_min <= std_max
  std = torch.linspace(std_max, std_min, T + 1)

  torch.manual_seed(seed)
  x_noised = torch.randn_like(x_truth)
  x = x_noised.clone()

  for i in range(T + 1):
    score = compute_score_image(x, x_truth, torch.tensor([std[i]])) # this will be where the NN model comes in
    x += dt * score
    if noise_on and i <= T:
      x += np.sqrt(2 * dt) * torch.randn_like(x)
  return x


# some visualizations
print('Un-annealed ODE-like')
x = follow_score_image(x_start, 0.5, 0.5, noise_on=False)
display.display(reverse_transform(x[0]))

print('Annealed ODE-like')
x = follow_score_image(x_start, 0.1, 5.0, noise_on=False)
display.display(reverse_transform(x[0]))

print('Un-annealed Langevin dynamics')
x = follow_score_image(x_start, 0.5, 0.5, noise_on=True)
display.display(reverse_transform(x[0]))

print('Annealed Langevin dynamics')
x = follow_score_image(x_start, 0.1, 5.0, noise_on=True)
display.display(reverse_transform(x[0]))

print('Note: this just a demo and does not suggest which sampling is superior')

# Sampling from a SE-3 Gaussian Distribution
def sample_from_se3_gaussian(x_tar, R_tar, std):
  '''
  x_tar: translational mean, (..., 3)
  R_tar: rotational mean, (..., 3, 3)
  std: standard deviation, (..., )
  '''

  x_eps = std[:, None] * torch.randn_like(x_tar)

  theta_eps = std[:, None] * torch.randn_like(x_tar)
  rot_eps = SO3().exp_map(theta_eps).to_matrix()

  _x = x_tar + x_eps # compose the translation
  _R = R_tar @ rot_eps # compose the rotation by matrix mutiplication
  return _x, _R


# another implementation using theseus built-in randn
def sample_from_se3_gaussian_with_theseus(x_tar, R_tar, std):
  '''
  x_tar: translational mean, (..., 3)
  R_tar: rotational mean, (..., 3, 3)
  std: standard deviation, (..., )
  '''
  batch_size = std.shape[0]
  x_eps = std[:, None] * torch.randn_like(x_tar)
  rot_eps = scale_rotations(SO3.randn(batch_size).to_matrix(), std)

  _x = x_tar + x_eps # compose the translation
  _R = R_tar @ rot_eps # compose the rotation
  return _x, _R


# using the complicated formula of IGSO3


# A helper function construct H from x and R
# H = [[R, x],
#      [0, 1]]
def construct_roto_trans(x, R):
  assert len(R.shape) == 3
  assert x.shape[0] == R.shape[0]
  batch_size = x.shape[0]

  H = torch.eye(4)[None, ...].repeat(batch_size, 1, 1)
  H[:, :3, :3] = R.clone()
  H[:, :3, -1] = x.clone()
  return H

torch.manual_seed(42)
B = 400
R_mu = SO3.rand(1).to_matrix().repeat(B, 1, 1) # mean rotation
x_mu = torch.randn(1, 3).repeat(B, 1) # mean translation

# rotation and translation combined in the H tensor (..., 4, 4)
H_mu = construct_roto_trans(x_mu, R_mu)
print('An example of SE(3) group element:')
print(H_mu[0:1])

# Visualizations of Gaussians on SO(3) centering at mean rotation with different std
stds = [1.0, 0.8, 0.5, 0.25, 0.1, 0.05]
rots, rots_with_theseus = [], []
for std in stds:

  __, R_samples = sample_from_se3_gaussian(x_mu, R_mu, std * torch.ones(B))
  __, R_samples_with_theseus = sample_from_se3_gaussian_with_theseus(x_mu, R_mu, std * torch.ones(B))
  rots.append(R_samples)
  rots_with_theseus.append(R_samples_with_theseus)

print('sample_from_se3_gaussian')
fig = plot_rotations(rots, labels=stds)
fig.to_html('se3_gaussian.html')

print('sample_from_se3_gaussian_with_theseus')
fig = plot_rotations(rots_with_theseus, labels=stds)
fig.to_html('se3_gaussian_th.html')

# Outputs: 
# An example of SE(3) group element:
# tensor([[[-0.7645,  0.1293, -0.6315, -0.8293],
#          [ 0.6156, -0.1438, -0.7748, -1.6137],
#          [-0.1910, -0.9811,  0.0303, -0.2147],
#          [ 0.0000,  0.0000,  0.0000,  1.0000]]])

# A spreadout SE(3) Gaussian, std = 0.4
torch.manual_seed(42)
x_samples, R_samples = sample_from_se3_gaussian(x_mu, R_mu, 0.4 * torch.ones(B))

H = construct_roto_trans(x_samples, R_samples)
H = torch.cat([H, H_mu[0:1]], dim=0)
colors = torch.zeros_like(H[:, :3, -1])
colors[-1, 0] = 1

scene = visualize_grasps(Hs=H, colors=colors.numpy(), show=False)
display.display(scene.show())


# A tight SE(3) Gaussian, std = 0.25
torch.manual_seed(42)
x_samples, R_samples = sample_from_se3_gaussian(x_mu, R_mu, 0.25 * torch.ones(B))

H = construct_roto_trans(x_samples, R_samples)
H = torch.cat([H, H_mu[0:1]], dim=0)
colors = torch.zeros_like(H[:, :3, -1])
colors[-1, 0] = 1

scene = visualize_grasps(Hs=H, colors=colors.numpy(), show=False)
display.display(scene.show())

print('Note that each fork is of the same size!')

# Evaluate log probability of SE(3) poses in SE(3) Gaussian distribution
def se3_log_probability_normal(x, R, x_tar, R_tar, std, eps=1e-6):
  '''
  x: translation samples
  R: rotation samples

  x_tar: mean translation of SE-3 gaussian
  R_tar: mean rotation of SE-3 gaussian
  std: standard deviation of the SE-3 gaussian
  '''
  assert x.shape == x_tar.shape
  assert R.shape == R_tar.shape

  # Mean rotation as theseus object
  _R_tar = SO3()
  _R_tar.update(R_tar)

  # rotation samples as theseus object
  _R = SO3()
  _R.update(R)
  R = _R

  # Compute distance in R^3 + SO(3)
  # Rotation distance
  R_tar_inv = _R_tar.inverse()
  dR = SO3()
  dR_rot = R_tar_inv.to_matrix() @ R.to_matrix()
  dR.update(dR_rot)
  dv = dR.log_map() # the vector representation for the rotation difference

  # translation distance
  dx = (x - x_tar)

  # 6D distance
  dist = torch.cat((dx, dv), dim=-1)

  # compute the log probability up to a constant term, which we don't care
  return -.5 * dist.pow(2).sum(-1) / (std.pow(2) + eps)


std = 0.25 * torch.ones(B)
log_prob = se3_log_probability_normal(x_samples, R_samples, x_mu, R_mu, std)

# probability of each sample comping from the SE-3 samples
colors = torch.zeros((B + 1, 3))
colors[:-1, 1] = (log_prob - log_prob.min())/(log_prob.max() - log_prob.min())
colors[:-1, 0] = 1. - (log_prob - log_prob.min())/(log_prob.max() - log_prob.min())

scene = visualize_grasps(Hs=H, colors=colors.numpy(), show=False)
display.display(scene.show())
print('These forks are colored by the log probability, the greener the greater the logp < 0')

# Move an SE(3) pose given the score of a Gaussian Distribution in SE(3)

# compute the SE(3) scores
def se3_score_normal(x, R, x_tar, R_tar, std):
  '''
  x: translational samples. (..., 3)
  R: rotational samples. (..., 3, 3)

  v: se3 scores. (..., 6)
  '''

  # theseus object
  _R = SO3()
  _R.update(R)
  R = _R

  # construct trainable 6D vector
  v = R.log_map()
  x_theta = torch.cat((x, v), dim=-1)
  x_theta.requires_grad_(True)

  # assign components from 6D vector
  # looks redundant but this preserves the gradient hook and computation graph
  x = x_theta[..., :3]
  R = SO3.exp_map(x_theta[..., 3:])

  # compute log probability with gradient hooked tensors
  d = se3_log_probability_normal(x, R, x_tar, R_tar, std)
  v = grad(d.sum(), x_theta, only_inputs=True)[0]
  return v

# (x, R) + v
def step(x, R, v):
    # compose rotations
    rot = SO3.exp_map(v[..., 3:]).to_matrix()
    R_1 = R @ rot

    # compose translations
    x_1 = x + v[...,:3]
    return x_1, R_1


# a helper function for scaling the roto-translation vector
# using the proper scaling of rotations
def scale_roto_trans_vec(v, scale):
  assert v.shape[0] == scale.shape[0]

  trans, roto = v[..., :3], v[..., 3:]

  # roto vector scaling
  R = SO3().exp_map(roto).to_matrix()
  R = scale_rotations(R, scale)
  roto = SO3(tensor=R).log_map()

  # trans vector scaling
  trans = trans * scale[..., None]

  return torch.cat((trans, roto), dim=-1)


# follow se3 scores, keeping intermediate states and outputs the scene
def follow_score_se3(x_truth, R_truth, std_min, std_max, T=2000, dt=0.001, noise_on=False, naive_scale=True, seed=41):

  assert x_truth.shape[0] == R_truth.shape[0] == 1
  H_truth = construct_roto_trans(x_truth, R_truth)

  # start with some random position and rotation in SE(3)
  torch.manual_seed(seed)
  R = SO3.rand(1).to_matrix() # the prior is USO3
  x = torch.randn(1, 3) # the prior is Normal

  # std schedules
  stds = torch.linspace(std_max, std_min, T + 1)
  sqrt2_dt = np.sqrt(2 * dt)

  # init SE3 components
  H_trj = torch.zeros(0, 4, 4)

  # following the scores
  for i in tqdm(range(T + 1)):
    H0 = construct_roto_trans(x.detach(), R.detach())
    H_trj = torch.cat((H_trj, H0), dim=0)

    v = se3_score_normal(x, R, x_truth, R_truth, std=torch.tensor([stds[i]]))

    _s = v * dt if naive_scale else scale_roto_trans_vec(v, torch.tensor([dt]))

    if noise_on and i < T:
      z = torch.randn_like(v)
      _s += sqrt2_dt * z if naive_scale else scale_roto_trans_vec(z, torch.tensor([sqrt2_dt]))

    # one step following the score
    x, R = step(x, R, _s)

  # for vis
  H = torch.cat((H_trj, H_truth), dim=0)
  colors = torch.zeros_like(H[:,:3,-1])
  colors[:-1, 1] = torch.linspace(0, 1, H_trj.shape[0])
  colors[:-1, 2] = 1 - torch.linspace(0, 1, H_trj.shape[0])
  colors[-1,0] = 1

  scene = visualize_grasps(Hs=H, colors=colors.numpy(), show=False)
  return H, scene

print('Un-annealed ODE-like with large std...')
__, scene = follow_score_se3(x_mu[:1, ...], R_mu[:1, ...], 0.5, 0.5, noise_on=False)
display.display(scene.show())

print('Un-annealed ODE-like with small std...')
__, scene = follow_score_se3(x_mu[:1, ...], R_mu[:1, ...], 0.1, 0.1, noise_on=False)
display.display(scene.show())

print('Annealed ODE-like')
__, scene = follow_score_se3(x_mu[:1, ...], R_mu[:1, ...], 0.1, 5.0, noise_on=False)
display.display(scene.show())


print('Un-annealed Langevin dyanmics with large std...')
__, scene = follow_score_se3(x_mu[:1, ...], R_mu[:1, ...], 0.5, 0.5, noise_on=True)
display.display(scene.show())

print('Un-annealed Langevin dyanmics with small std...')
__, scene = follow_score_se3(x_mu[:1, ...], R_mu[:1, ...], 0.1, 0.1, noise_on=True)
display.display(scene.show())

print('Annealed Langevin dyanmics')
__, scene = follow_score_se3(x_mu[:1, ...], R_mu[:1, ...], 0.1, 5.0, noise_on=True)
display.display(scene.show())

# Training a Toy SE(3) Diffusion Model

# getting the data
def get_sample_from_data(B=100):
  x_data = torch.Tensor([[0.3, 0.3, 0.3],
                          [-0.5, 1.2, -0.7]])
  theta_data = torch.Tensor([[0., 0.0, 0.0],
                              [-0.3, 1.2, -0.4]])
  R_data = SO3().exp_map(theta_data).to_matrix()
  idx = torch.randint(0, 2, (B, ))
  _x = x_data[idx, ...]
  _R = R_data[idx, ...]
  return _x, _R


# defines the scheduling of std schedule with SDE with no drift
# this is the variance schedule we chose
def marginal_prob_std(t, sigma=0.5):
  return torch.sqrt((sigma ** (2 * t) - 1.) / (2. * np.log(sigma)))


# Define the layer and model

# Time step embedding
class GaussianFourierProjection(nn.Module):
  '''Gaussian random features for encoding time steps.
  '''
  def __init__(self, embed_dim, scale=30.):
    super().__init__()
    self.W = nn.Parameter(torch.randn(embed_dim // 2) * scale, requires_grad=False) # fixed random projection

  def forward(self, x):
    x_proj = torch.einsum('...,b->...b', x, self.W) * 2 * torch.pi
    return torch.cat([torch.sin(x_proj), torch.cos(x_proj)], dim=-1)


# Naive all linears
class NaiveSE3DiffusionModel(nn.Module):
  '''Basic NN with linears
  input the noised x (B, 3) and R (B, 3, 3) at time t (B, )
  output the predicted scores v (B, 6)
  '''
  def __init__(self):
    super().__init__()

    input_size = 12 # we take a translation and flattened rotation
                    # one can do a 6-dim where we take the Log of the rotation
    enc_dim = 128
    output_size = 6

    self.network = nn.Sequential(
        nn.Linear(2 * enc_dim, 128),
        nn.ReLU(),
        nn.Linear(128, 256),
        nn.ReLU(),
        nn.Linear(256, output_size)
    )

    # Time Embedings Encoder
    self.time_embed = nn.Sequential(
        GaussianFourierProjection(embed_dim=enc_dim),
        nn.Linear(enc_dim, enc_dim),
        nn.SiLU(),
    )
    self.x_embed = nn.Sequential(
        nn.Linear(input_size, enc_dim),
        nn.SiLU(),
    )


  def forward(self, x, R, t):
    std = marginal_prob_std(t)
    x_R_input = torch.cat((x, R.reshape(R.shape[0], -1)), dim=-1)
    z = self.x_embed(x_R_input)
    z_time = self.time_embed(t)
    z_in = torch.cat((z, z_time),dim=-1)
    v = self.network(z_in)

    # the 1/v scaling is necessary for numerical stability
    # as we don't want the NN to predict scores say, from 0.001 to 100.0
    return v / (std[..., None].pow(2))


# Training
model = NaiveSE3DiffusionModel()
optimizer = torch.optim.AdamW(model.parameters(), lr=0.0005)

K = 1000
B = 500
EPS = 1e-3
loss_trj = torch.zeros(0)
for k in tqdm(range(K)):

    t = (1 - EPS) * torch.rand(B) + EPS # t ~ 0 will cause numerical instability
    std = marginal_prob_std(t) # compute scheuling of std at t=t, increasing with t
    x, R = get_sample_from_data(B) # batch samples
    x_eps, R_eps = sample_from_se3_gaussian(x, R, std) # noised samples

    v_tar = se3_score_normal(x_eps, R_eps, x_tar=x, R_tar=R, std=std) # estimate scores of noised samples
    v_pred = model(x_eps, R_eps, t) # predicted scores from model
    loss = std ** 2 * (((v_pred - v_tar) ** 2).sum(-1)) # score matching loss
    loss_trj = torch.cat((loss_trj, loss.mean().detach()[None]), dim=0)

    # Backward pass and optimization
    optimizer.zero_grad()
    loss.mean().backward()
    optimizer.step()

plt.plot(loss_trj)
plt.show()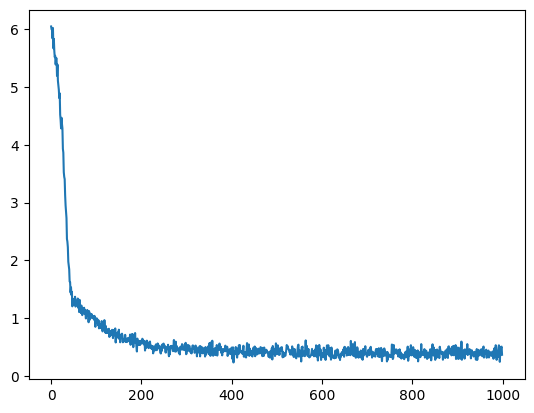

# Given the model run reverse sampling using the step function we defined
def sample_se3(model, data_gen, B=B, T=1000, dt=0.001, eps=1e-3, noise_on=False, naive_scale=True, seed=37):

  # random starting point
  torch.manual_seed(seed)
  R0 = SO3.rand(B).to_matrix()
  x0 = torch.randn(B, 3)

  for t in range(T):
    k = (T - t)/T + eps

    v = model(x0, R0, t=k * torch.ones(B))
    _s = v * dt if naive_scale else scale_roto_trans_vec(v, dt * torch.ones(B, ))

    if noise_on and t != T - 1:
      z = torch.randn_like(v)
      _s += np.sqrt(2 * dt) * z if naive_scale else scale_roto_trans_vec(z, np.sqrt(2 * dt) * torch.ones(B, ))

    x0, R0 = step(x0, R0, _s)

  # generated samples (red)
  H_gen = construct_roto_trans(x0.detach(), R0.detach())
  colors_gen = torch.zeros((B, 3))
  colors_gen[:,0] = 1

  # real samples (green)
  xd, Rd = data_gen(B=10)
  H_dat = construct_roto_trans(xd, Rd)
  colors_dat = torch.zeros((10, 3))
  colors_dat[:,1] = 1

  H = torch.cat((H_gen, H_dat), dim=0)
  c = torch.cat((colors_gen, colors_dat), dim=0)

  scene = visualize_grasps(Hs=H, colors=c.numpy(), show=False)
  return H_gen, scene

print('Sampling from trained model by following score prediction')
__, scene = sample_se3(model, get_sample_from_data, noise_on=False)
display.display(scene.show())

print('Sampling from trained model by Langevin dynamics')
H, scene = sample_se3(model, get_sample_from_data, noise_on=True)
display.display(scene.show())
plot_rotations([R_dummy] + [H[..., :3, :3]] + [get_sample_from_data(10)[1]])

# try different distributions
def get_sample_from_data_2(B=100):
    x_data = torch.Tensor([[0.3, 0.3, 0.3],
                           [-0.5, 1.2, -0.7],
                           [3.1, 1.3, -2.4], # this one is significantly more further away
                           [-0.3, 1.2, 0.4]])
    theta_data = torch.Tensor([[0., 0.0, 0.0],
                               [-0.3, 1.2, -0.4],
                               [0.3, -1., -1.4],
                               [-0.5, 1.2, 0.7]])

    R_data = SO3().exp_map(theta_data).to_matrix()
    idx = torch.randint(0, 4, (B,))
    _x = x_data[idx, :]
    _R = R_data[idx, ...]
    return _x, _R


# the same training, just copied and pasted here
model = NaiveSE3DiffusionModel()
optimizer = torch.optim.AdamW(model.parameters(), lr=0.0005)


K = 1000
B = 500
loss_trj = torch.zeros(0)
for k in tqdm(range(K)):

    t = (1 - EPS) * torch.rand(B) + EPS
    std = marginal_prob_std(t)
    x, R = get_sample_from_data_2(B)
    x_eps, R_eps = sample_from_se3_gaussian(x, R, std)

    v_tar = se3_score_normal(x_eps, R_eps, x_tar=x, R_tar=R, std=std)
    v_pred = model(x_eps, R_eps, t)
    loss = std ** 2 *(((v_pred - v_tar) ** 2).sum(-1))
    loss_trj = torch.cat((loss_trj, loss.mean().detach()[None]), dim=0)

    optimizer.zero_grad()
    loss.mean().backward()
    optimizer.step()

plt.plot(loss_trj)
plt.show()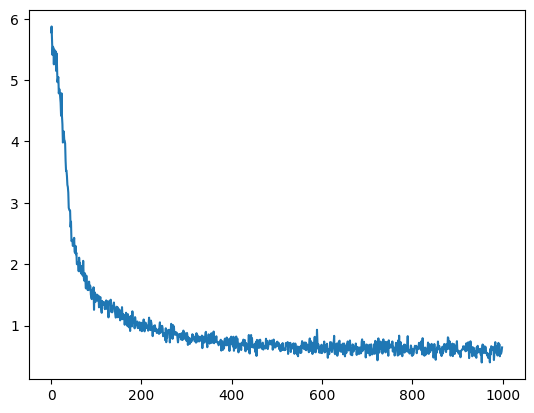

print('Sampling from trained model by following score prediction')
__, scene = sample_se3(model, get_sample_from_data_2, noise_on=False)
display.display(scene.show())


print('Sampling from trained model by Langevin dynamics')
H, scene = sample_se3(model, get_sample_from_data_2, noise_on=True)
display.display(scene.show())

plot_rotations([R_dummy] + [H[..., :3, :3]] + [get_sample_from_data_2(20)[1]])

print()
print('Notice there is a relative sampling bias with respective to the more distant point')
print('This is because for translational sampling, the more distance from the original, the less likely it will be achieved')
print('One can simply make the system of zero COM.')

# Let's redo th training by centering the SE(3) distribution at origin

offset = torch.tensor([0.6500, 1.0000, -0.6000])

model = NaiveSE3DiffusionModel()
optimizer = torch.optim.AdamW(model.parameters(), lr=0.0005)

# again copied and pasted
# should've put this into a function but well..
K = 1000
B = 500
loss_trj = torch.zeros(0)
for k in tqdm(range(K)):

    t = (1 - EPS) * torch.rand(B) + EPS
    std = marginal_prob_std(t)
    x, R = get_sample_from_data_2(B)

    # the only difference is the centering
    x -= offset

    x_eps, R_eps = sample_from_se3_gaussian(x, R, std)
    v_tar = se3_score_normal(x_eps, R_eps, x_tar=x, R_tar=R, std=std)
    v_pred = model(x_eps, R_eps, t)
    loss = std ** 2 *(((v_pred - v_tar) ** 2).sum(-1))
    loss_trj = torch.cat((loss_trj, loss.mean().detach()[None]), dim=0)

    # Backward pass and optimization
    optimizer.zero_grad()
    loss.mean().backward()
    optimizer.step()

plt.plot(loss_trj)
plt.show()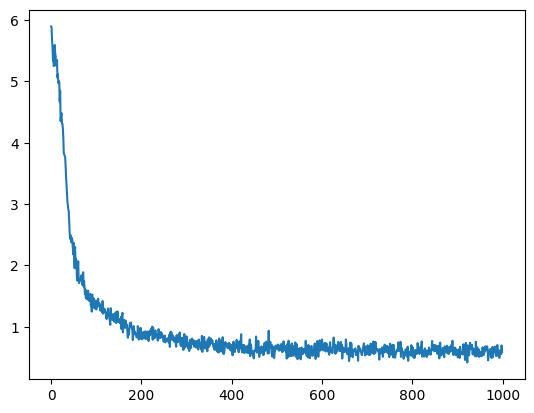

print('Sampling from trained model by Langevin dynamics')
H, scene = sample_se3(model, get_sample_from_data_2, noise_on=True)
display.display(scene.show())
plot_rotations([R_dummy] + [H[..., :3, :3]] + [get_sample_from_data_2(20)[1]])
print()
print('The green forks are from un-centered distribution')
print('Notice that the sampling becomes more balanced by just centering the distribution')
print('There are ways to improve the sampling, like scaling.')
print('Because the roto-translation are coupled, now we have a more balanced samples for the orientation as well.')

print()
print('There are many ways to overcome this, like scaling, sample and recentering, decoupling')

# Let's use a more complicated SE(3) distribution - protein

import pickle

retrain = False # turn this on if you want to train it yourself

# rotation from 3 points using Gram–Schmidt to construct local basis
# a protein local frame can be constructed using C-alpha, N and C
def from_3_points(
        p_neg_x_axis: torch.Tensor,
        origin: torch.Tensor,
        p_xy_plane: torch.Tensor,
        eps: float = 1e-8
    ):
        """
            Implements algorithm 21. Constructs transformations from sets of 3
            points using the Gram-Schmidt algorithm.

            Args:
                p_neg_x_axis: [*, 3] coordinates
                origin: [*, 3] coordinates used as frame origins
                p_xy_plane: [*, 3] coordinates
                eps: Small epsilon value
            Returns:
                A transformation object of shape [*]
        """
        p_neg_x_axis = torch.unbind(p_neg_x_axis, dim=-1)
        origin = torch.unbind(origin, dim=-1)
        p_xy_plane = torch.unbind(p_xy_plane, dim=-1)

        e0 = [c1 - c2 for c1, c2 in zip(origin, p_neg_x_axis)]
        e1 = [c1 - c2 for c1, c2 in zip(p_xy_plane, origin)]

        denom = torch.sqrt(sum((c * c for c in e0)) + eps)
        e0 = [c / denom for c in e0]
        dot = sum((c1 * c2 for c1, c2 in zip(e0, e1)))
        e1 = [c2 - c1 * dot for c1, c2 in zip(e0, e1)]
        denom = torch.sqrt(sum((c * c for c in e1)) + eps)
        e1 = [c / denom for c in e1]
        e2 = [
            e0[1] * e1[2] - e0[2] * e1[1],
            e0[2] * e1[0] - e0[0] * e1[2],
            e0[0] * e1[1] - e0[1] * e1[0],
        ]

        rots = torch.stack([c for tup in zip(e0, e1, e2) for c in tup], dim=-1)
        rots = rots.reshape(rots.shape[:-1] + (3, 3))
        return rots

# an in-house preprocessed antibody structure
# this should be provided with the notebook
data = pickle.load(open('./AFQ82415.pkl', 'rb'))
coordinates = torch.from_numpy(data['atom_positions'][:101, :, :3]) # N, Ca, C

rots = from_3_points(coordinates[:, 0], coordinates[:, 1], coordinates[:, 2])
trans = coordinates[..., 1, :] / 10. # we need to scale this in order to get a more balanced samples
p = construct_roto_trans(trans, rots)

# interpolate between residues to augment the data
t1, t2 = trans[:-1, ...], trans[1:, ...]
r1, r2 = rots[:-1, ...], rots[1:, ...]

for w in torch.linspace(0.1, 1.0, 20):
  t = w * t1 + (1. - w) * t2
  r = slerp(r2, r1, torch.ones(100) * w)
  p = torch.cat((p, construct_roto_trans(t, r)))

scene = visualize_grasps(p, show=False)
display.display(scene.show())

# get samples from backbone
prot = construct_roto_trans(trans, rots)
print(prot.shape)

def get_sample_from_protein(prot=prot, B=500):

  n = prot.shape[0]
  idx = torch.randint(0, n, (B, ))
  H = prot[idx, ...]
  _x = H[:, :3, -1]
  _R = H[:, :3, :3]
  return _x, _R


# a deeper model
# We just naively stacked more Linears in between
class NaiveSE3DiffusionModel2(nn.Module):
    def __init__(self):
        super().__init__()

        input_size = 12
        enc_dim = 128
        output_size = 6

        self.network1 = nn.Sequential(
            nn.Linear(2*enc_dim, 128),
            nn.ReLU(),
            nn.Linear(128, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, enc_dim)
        )

        self.network2 = nn.Sequential(
            nn.Linear(2*enc_dim, 128),
            nn.ReLU(),
            nn.Linear(128, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, output_size)
        )

        ## Time Embedings Encoder ##
        self.time_embed = nn.Sequential(
            GaussianFourierProjection(embed_dim=enc_dim),
            nn.Linear(enc_dim, enc_dim),
            nn.SiLU(),
        )
        self.x_embed = nn.Sequential(
            nn.Linear(input_size, enc_dim),
            nn.SiLU(),
        )

    def marginal_prob_std(self, t, sigma=0.5):
        return torch.sqrt((sigma ** (2 * t) - 1.) / (2. * np.log(sigma)))

    def forward(self, x, R, t):
        std = self.marginal_prob_std(t)
        x_R_input = torch.cat((x, R.reshape(R.shape[0], -1)), dim=-1)
        z = self.x_embed(x_R_input)
        z_time = self.time_embed(t)
        z_in = torch.cat((z, z_time),dim=-1)
        z = self.network1(z_in)
        z_in = torch.cat((z, z_time),dim=-1)
        v = self.network2(z_in)
        return v/(std[:,None].pow(2))

if retrain:
    torch.manual_seed(42)

    model = NaiveSE3DiffusionModel2()
    optimizer = torch.optim.AdamW(model.parameters(), lr=0.0005)

    K = 30000
    B = 1000
    loss_trj = torch.zeros(0)
    for k in tqdm(range(K)):

        t = (1 - EPS) * torch.rand(B) + EPS # t ~ 0 will cause numerical instability
        std = marginal_prob_std(t) # compute scheuling of std at t=t, increasing with t
        x, R = get_sample_from_protein(B=B) # batch samples

        x_eps, R_eps = sample_from_se3_gaussian(x, R, std) # noised samples

        v_tar = se3_score_normal(x_eps, R_eps, x_tar=x, R_tar=R, std=std) # estimate scores of noised samples

        v_pred = model(x_eps, R_eps, t) # predicted scores from model

        loss = std ** 2 * (((v_pred - v_tar) ** 2).sum(-1)) # score matching loss
        loss_trj = torch.cat((loss_trj, loss.mean().detach()[None]), dim=0)

        # Backward pass and optimization
        optimizer.zero_grad()
        loss.mean().backward()
        optimizer.step()

    plt.plot(loss_trj)
    plt.show()

    # torch.save(model.state_dict(), 'model.pt')

if not retrain:
  model = NaiveSE3DiffusionModel2()
  model.load_state_dict(torch.load('model.pt'))
H, __ = sample_se3(model, get_sample_from_protein, noise_on=False, T=1000, B=500)
H2, __ = sample_se3(model, get_sample_from_protein, noise_on=False, T=1000, B=500)

H = torch.cat((H, H2), dim=0)
colors = torch.zeros((1101, 3))
colors[:1000, 0] = 1.0
colors[1000:, 1] = 1.0
scene = visualize_grasps(torch.cat((H, prot), dim=0), colors=colors.numpy(), show=False)
display.display(scene.show())

colors = torch.zeros((H.shape[0] + p.shape[0], 3))
colors[:1000, 0] = 1.0
colors[1000:, 1] = 1.0
scene = visualize_grasps(torch.cat((H, p), dim=0), colors=colors.numpy(),show=False)
display.display(scene.show())
print('Green is the grund truth')