Training GNN for Stability Prediction
Mutations of a protein affect the protein stability, via changing the local interactions among neighboring residues. This mutation effect has been hard to predict especially in the case of protein conformational changes becuase of limited experimental data available. Recently, Tsuboyama et al. reported a large study of protein folding stability and made the data available.
It might be interesting to model these protein stability data (dG) using the structure and graph neural networks. The notebook and associated subset of the data can be found here. I was using a structure given from the paper: HEEH_KT_rd6_4322.pdb and the cleaned dG data test_dG_data.csv. Each entry represent the single point mutation and corresponding dG. The goal is to build a graph neural network that learns the local neighborhood of the point mutation and predict the stability effect.
0. Dependencies
Building a graph from pdb requires many dependencies for the interaction edges. Here I just used minimal functions to construct the edges.
If ones uses edge features in the message passing, I would recommend build all edges. Otherwise, these edges might result in over-smoothing in message passing.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Dependencies
import os, torch, copy, Bio, logging
logging.getLogger('matplotlib').setLevel(level=logging.CRITICAL)
logging.getLogger('graphein').setLevel(level=logging.CRITICAL)
import pandas as pd
import numpy as np
import networkx as nx
from functools import partial
from tqdm.auto import tqdm
from torch_geometric.nn import GCNConv
from torch_geometric.loader import DataLoader, DataListLoader
from torch_geometric.data import Data
from torch_geometric.utils import add_self_loops
from torch_scatter import scatter_mean, scatter_sum
from graphein.protein.config import ProteinGraphConfig
from graphein.protein.graphs import construct_graph
from graphein.protein.edges.distance import *
from graphein.protein.features.nodes.amino_acid import amino_acid_one_hot
from graphein.protein.visualisation import plotly_protein_structure_graph
from graphein.ml.conversion import GraphFormatConvertor
node_edge_graph_funcs = {'edge_construction_functions': [add_peptide_bonds,
add_hydrogen_bond_interactions,
add_backbone_carbonyl_carbonyl_interactions,
partial(add_distance_threshold, long_interaction_threshold=5, threshold=8.0)],
'node_metadata_functions': [amino_acid_one_hot]}
CONFIG = ProteinGraphConfig(**node_edge_graph_funcs)
1. Example Data
I merged the tables from Raw_NGS_count_tables, K50_dG_tables and pull out one structure from AlphaFold_model_PDBs for this example.
The test_dG_data.csv is the simplified file.
1
2
3
4
5
6
# tables for dG
data = pd.read_csv('test_dG_data.csv')
data = data.dropna().iloc[3:]
data['mutation'] = data['name'].apply(lambda x: x.split('_')[-1])
print(data.shape)
data.head(2)
Output:
(946, 3)
Now, construct the protein graph using Graphein.
1
2
3
4
5
6
7
8
9
10
11
12
13
# Construct graph from PDB
g = construct_graph(pdb_path='HEEH_KT_rd6_4322.pdb', config=CONFIG)
# visualize as point cloud graph in 3d
p = plotly_protein_structure_graph(g, colour_edges_by="kind",
colour_nodes_by="element_symbol",
label_node_ids=False,
node_size_min=5,
node_alpha=0.85,
node_size_multiplier=1,
plot_title="HEEH_KT_rd6_4322")
p.show()
Output:
Does it look like 2 alpha helices and 2 small beta sheets, like below?
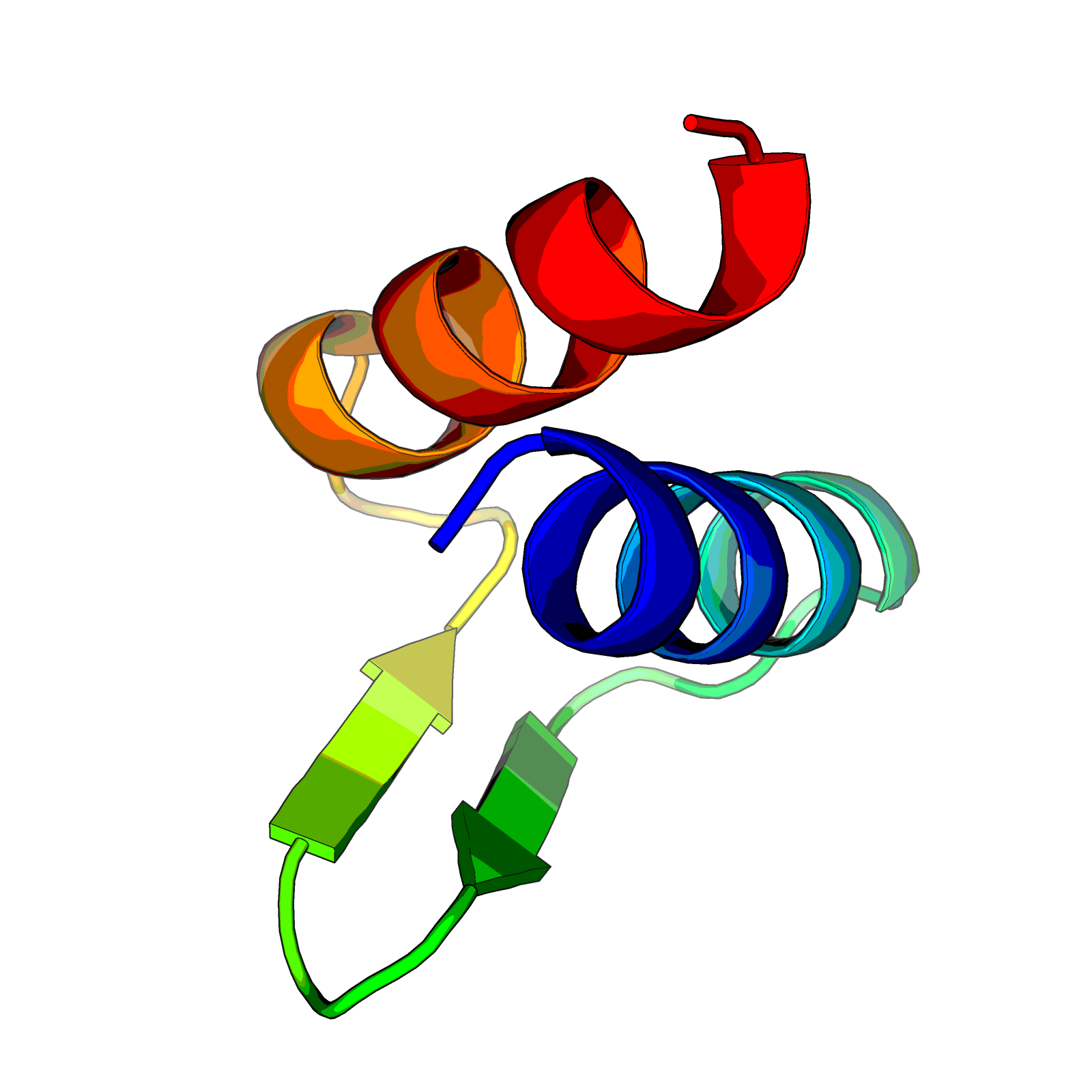
Now g is a networkx graph and we can take a look at what it contains.
1
2
3
print(g.nodes['A:SER:1']) # node features
print(g.edges[('A:SER:1', 'A:GLU:2')]) # edge_features
# g.graph contains the original pdb info
Output:
{'chain_id': 'A', 'residue_name': 'SER', 'residue_number': 1, 'atom_type': 'CA', 'element_symbol': 'C', 'coords': array([1.458, 0. , 0. ]), 'b_factor': 0.0, 'amino_acid_one_hot': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0])}
{'kind': {'bb_carbonyl_carbonyl', 'peptide_bond'}, 'distance': 3.8009521175621246}2. Data Wrangling
Here I defined some functions for arranging the data intoeasy-to-work-with format, including the pytorch data object GFocus.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
def one2three(resn):
return Bio.SeqUtils.seq3(resn).upper()
def get_aa_one_hot(resn):
if len(resn) == 3: aa = resn
elif len(resn) == 1: aa = one2three(resn)
else: NotImplementedError()
return amino_acid_one_hot('', {'residue_name': aa})
def get_node_features(g, field):
node = list(g.nodes)[0]
assert field in g.nodes[node]
return torch.from_numpy(np.array([g.nodes[node][field] for node in g.nodes]))
def graph2data(g, focus, fields=['amino_acid_one_hot']):
assert len(g.nodes()) > 0
assert focus in g.nodes
d = GraphFormatConvertor('nx', 'pyg').convert_nx_to_pyg(g)
d.x = torch.cat([get_node_features(g, field) for field in fields], dim=1).to(torch.float)
d.focus = list(g.nodes).index(focus)
return d
# The Customized Focused Graph
# The focus is the node being mutated
class GFocus(Data):
def __init__(self, data):
super().__init__()
attrs = ['x', 'edge_index', 'focus', 'y', 'name', 'mut']
if data is not None:
for attr in attrs: setattr(self, attr, getattr(data, attr))
def __inc__(self, key, value, *args, **kwargs):
if key == 'focus': return self.x.shape[0]
else: return super().__inc__(key, value, *args, **kwargs)
def mutate_aa(g, mut):
chain = list(g.nodes)[0][0]
wt, resi, mt = one2three(mut[0]), mut[1:-1], one2three(mut[-1])
node, new_node = f'{chain}:{wt}:{resi}', f'{chain}:{mt}:{resi}'
assert node in g.nodes
ng = nx.relabel_nodes(g, {node: new_node})
ng.nodes[new_node]['amino_acid_one_hot'] = get_aa_one_hot(mt)
return ng, new_node
def generate_dataloader(df, g, batch_size, verbose=True):
# only do that for mutations, ignore insert or dele for now
# insertion can be: duplicating neighbor residues then resample edges
# deletion might be tricky: keep neighbor info then deleting the node then use neighbors for prediction
assert len(set.intersection(set(['mutation', 'deltaG']), set(data.columns))) == 2
datalist = []
for i in df.index:
mut, dg = df.loc[i, ['mutation', 'deltaG']]
if mut[0].islower(): continue
# just skipping some "mutations" that does not pass the assert
try:
ng, new_node = mutate_aa(g, mut)
d = graph2data(ng, new_node)
d.y = dg
d.mut = mut
except:
if verbose: print(f'Cannot process {mut}')
continue
datalist.append(GFocus(d))
return DataLoader(datalist, batch_size=batch_size, shuffle=True, follow_batch='x')
Now we can create a data loader for training.
1
2
3
4
5
# data loader
dataloader = generate_dataloader(data, g, 32, verbose=False)
batch = next(iter(dataloader))
print(len(dataloader))
print(batch)
Output:
26
GFocusBatch(x=[1376, 20], x_batch=[1376], edge_index=[2, 2880], focus=[32], y=[32], name=[32], mut=[32], batch=[1376], ptr=[33])3. Naive Graph Neural Network Model
Here I used 4 simple layers:
- Pre: Preprocessing
- GNN: Message passing layers
- Neighborhood: Neighbor aggregation
- Head: Regression head
1. Preprocessing layer
This layer processes the node features using 2 Linear layers. Or one can just use torch.nn.Embedding layer, if the node features are one-hot or discrete.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Pre(torch.nn.Module):
def __init__(self, in_dim, hidden_dim):
super(Pre, self).__init__()
self.in_dim = in_dim
self.hidden_dim = hidden_dim
self.layers = torch.nn.ModuleList([torch.nn.Linear(in_dim, hidden_dim),
torch.nn.SiLU(),
torch.nn.Linear(hidden_dim, hidden_dim)])
def forward(self, x):
for layer in self.layers: x = layer(x)
return x
2. Message Passing Layers
This is the message passing operation by the simplest GCNConv graph convolution layer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class GNN(torch.nn.Module):
def __init__(self, hidden_dim, hops=3):
super(GNN, self).__init__()
# self.in_dim = in_dim
self.hidden_dim = hidden_dim
self.hops = hops
gnn_layers, bn_layers, act_layers = [], [], []
for __ in range(hops):
gnn_layers.append(GCNConv(hidden_dim, hidden_dim, add_self_loops=True))
bn_layers.append(torch.nn.BatchNorm1d(hidden_dim))
act_layers.append(torch.nn.Sigmoid())
self.gnn_layers = torch.nn.ModuleList(gnn_layers)
self.bn_layers = torch.nn.ModuleList(bn_layers)
self.act_layers = torch.nn.ModuleList(act_layers)
def forward(self, x, edge_index):
for i in range(self.hops): x = self.bn_layers[i](self.act_layers[i](self.gnn_layers[i](x, edge_index)))
return x
3. Local Neighborhood Aggregation
This might be tricky because given different mutation position, the focused neighborhood changes and indexed by neighbor_idx. The GFocus data class has this focus index and is colleated following minibatches of the graphs.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# get focus
def get_focus(edge_index, focus, hop=2):
idx = focus.clone()
row, col = edge_index
for __ in range(hop): idx = torch.cat([idx, col[torch.isin(row, idx)], row[torch.isin(col, idx)]], dim=0)
return idx.unique().to(torch.long)
class NeighborHood(torch.nn.Module):
def __init__(self, hidden_dim, out_dim, aggr='sum', hop=2):
super(NeighborHood, self).__init__()
assert aggr in ['mean', 'sum']
self.hidden_dim = hidden_dim
self.out_dim = out_dim
self.aggr = aggr
self.hop = hop
self.phi = torch.nn.Linear(hidden_dim, hidden_dim)
self.act_phi = torch.nn.SiLU()
self.bn_phi = torch.nn.BatchNorm1d(hidden_dim)
self.psi = torch.nn.Linear(hidden_dim, out_dim)
self.act_psi = torch.nn.SiLU()
def forward(self, x, edge_index, focus, batch):
neighbor_idx = get_focus(edge_index, focus)
message = self.bn_phi(self.act_phi(self.phi(x[neighbor_idx])))
if self.aggr == 'mean': message = scatter_mean(message, batch[neighbor_idx], dim=0)
elif self.aggr == 'sum': message = scatter_sum(message, batch[neighbor_idx], dim=0)
else: raise NotImplementedError()
out = self.act_psi(self.psi(message))
return out
4. Regression Head:
This is nothing but a prediction head from the embeddings of the focused neighborhood.
1
2
3
4
5
6
7
8
9
10
11
12
13
class RegressionHead(torch.nn.Module):
def __init__(self, hidden_dim):
super(RegressionHead, self).__init__()
self.hidden_dim = hidden_dim
self.layers = torch.nn.ModuleList([torch.nn.Linear(hidden_dim, hidden_dim),
torch.nn.SiLU(),
torch.nn.Linear(hidden_dim, 1)])
def forward(self, x):
for layer in self.layers: x = layer(x)
return x.view(-1)
5. Full Model and Loss
The full model StabilityGNN is now:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# full model
class StabilityGNN(torch.nn.Module):
def __init__(self, in_dim=20, hidden_dim=32, out_dim=64, hops=3):
super(StabilityGNN, self).__init__()
self.in_dim = in_dim
self.hidden_dim = hidden_dim
self.out_dim = out_dim
self.hops = hops
self.pre = Pre(in_dim, hidden_dim)
self.gnn = GNN(hidden_dim)
self.nh = NeighborHood(hidden_dim, out_dim)
self.head = RegressionHead(out_dim)
def forward(self, x, edge_index, focus, batch):
processed_x = self.pre(x)
node_embeds = self.gnn(processed_x, edge_index)
focus_embeds = self.nh(node_embeds, edge_index, focus, batch)
return focus_embeds, self.head(focus_embeds)
Since this is a regression task, I used the MSELoss
1
loss = torch.nn.MSELoss()
Now Let’s test the functionalities of these layers and their inputs and outputs.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# testing the functionalities of the layers
# Pre
pre = Pre(20, 32)
processed_x = pre(batch.x)
# GNN
gnn = GNN(32)
x = gnn(processed_x, batch.edge_index)
# Neighborhood
nh = NeighborHood(32, 64)
out = nh(x, batch.edge_index, batch.focus, batch.x_batch)
# RegressionHead
rh = RegressionHead(64)
pred = rh(out)
1
2
3
4
5
6
# testing the whole model
sgnn = StabilityGNN()
focus_embeds, pred = sgnn(batch.x, batch.edge_index, batch.focus, batch.x_batch)
assert focus_embeds.shape == (32, 64)
assert pred.shape[0] == 32
4. Training
Training the neighborhood embeddings to fit the dG locally on cpu… Took ~5 min for training with 800 (tiny) mutated graphs.
I was training this small example on CPU. If one wants to train on GPU, just .to('cuda')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# using naive model
stability_gnn = StabilityGNN()
mse_loss = torch.nn.MSELoss()
l1_loss = torch.nn.L1Loss()
nepochs = 1000
lr, wd = 1e-4, 1e-3
loss_type = 'L2'
log_every = int(np.floor(nepochs / 20))
optimizer = torch.optim.AdamW(stability_gnn.parameters(), lr=lr, weight_decay=wd)
for epoch in tqdm(range(nepochs + 1), desc='Training Stability GNN'):
losses = []
for batch in dataloader:
optimizer.zero_grad()
__, pred = stability_gnn(batch.x, batch.edge_index, batch.focus, batch.x_batch)
loss = mse_loss(pred, batch.y.to(torch.float)) if loss_type == 'L2' else l1_loss(pred, batch.y.to(torch.float))
loss.backward()
optimizer.step()
losses.append(loss.item())
avg_loss = np.array(losses).mean()
if epoch % log_every == 0: print(f'-- Epoch = {epoch}, MSE-Loss = {avg_loss}')
Output:
-- Epoch = 0, MSE-Loss = 5.007125299710494
-- Epoch = 50, MSE-Loss = 0.3031598604642428
-- Epoch = 100, MSE-Loss = 0.22531221978939497
-- Epoch = 150, MSE-Loss = 0.1948822490297831
-- Epoch = 200, MSE-Loss = 0.18019723892211914
-- Epoch = 250, MSE-Loss = 0.16349028222835982
-- Epoch = 300, MSE-Loss = 0.16791437165095255
-- Epoch = 350, MSE-Loss = 0.14197989237996247
-- Epoch = 400, MSE-Loss = 0.16626639348956254
-- Epoch = 450, MSE-Loss = 0.13275881555791086
-- Epoch = 500, MSE-Loss = 0.14490264081037962
-- Epoch = 550, MSE-Loss = 0.11256958214709392
-- Epoch = 600, MSE-Loss = 0.13622687069269326
-- Epoch = 650, MSE-Loss = 0.10607394826813386
-- Epoch = 700, MSE-Loss = 0.11214157938957214
-- Epoch = 750, MSE-Loss = 0.103588092355774
-- Epoch = 800, MSE-Loss = 0.11125421910904922
-- Epoch = 850, MSE-Loss = 0.09300274430559231
-- Epoch = 900, MSE-Loss = 0.11821510571126755
-- Epoch = 950, MSE-Loss = 0.15214177851493543
-- Epoch = 1000, MSE-Loss = 0.09064253620230235It seems like for these small singly mutated graphs, the model can learn the stability from local neighorhood embeddings. In another experiment, I was getting < 0.05 MSE loss. It might be interesting to test the trained model on an independent protein structures and see how it performs and if the neighborhood embeddings can be generalized.
5. Final Note
The StabilityGNN is just a naive model for this task with minimal inductive bias. I ran it serval times and I could get down to mse < 0.1 in 1000 epochs just using one-hot.
The model assumes identical conformation upon mutation, which is not always the case. That is why more complex structural modeling tools, such as Rosetta or Molecular Dynamics simulations were developed and used to model slight to drastic conformational changes.
The focus only consider k-hop neighbor, if k=0 it might just learn the PSSM of the position. If k > 2, the neighborhood information might be over-smoothed and is hard to generalize. Moreover, there are some cases where allosterics is critical in protein stability; such long-range interaction might help in stabilizing the proteins and undermine the naive assumption of this GNN model.
There can be multiple ways to improve / train the model, I’ll not reveal too much on that then..
The complete notebook can be found here.