EPI-EPMP Multitasking Model
The EPI-EPMP multitasking model was proposed by this paper. The model is based on message-passing neural networks; it takes antibody and antigen structures as input and predicts the paratope on the antibody and epitope on the antigen. The model architecture is shown below, which is the Fig. 2 of the original paper.
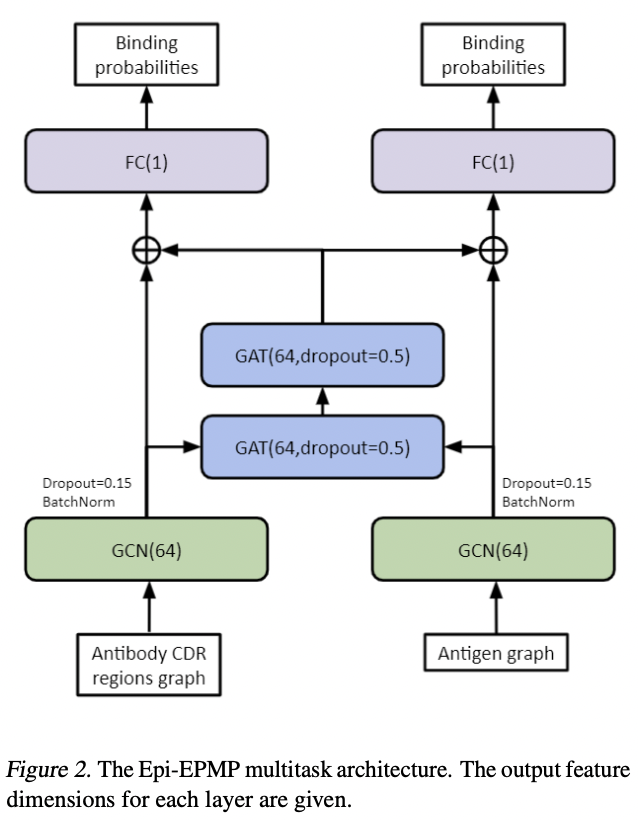
The model uses 2 different graph neural networks to process the antibody and antigen structure separately to get node embeddings for each residues. Then these nodes were used to construct a bipartite graph, similar to the old recommender system. The antigen and antibody node embeddings are passed around with graph attentional network (GAT) to obtain a final embedding for predicting binding probability of both paratopes and epitopes.
The benefit of such model is that it does not assume or sample relative orientations between antibody and antigen, which can be quite computationally expensive. It aims to do message-passing between antigen and antibody residues and determines the epitope and paratope from the mutual structural context.
I will use pyotrch-geometric(PyG) to build the batched data and EPI-EPMP model.
1. Data: Graph Pairing
For the model, one data point is one (antibody, antigen) pair. We have to build a paired data with minibatching. The tricky part is that antibody and antigen might have different number of residues, so we need to first take care of them separately.
Let’s assume that one can transform a protein structure data (i.e. atomic coordinates, PDBs) into a featurized graph G with node feature x, edge index edge_index. The Graphein package is one of the cool packages for this purpose. The following AbAgPair data class builds the paired graph:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from torch_geometric.data import Data
class AbAgPair(Data):
def __init__(self, antigen, antibody):
super().__init__()
# antigen: add prefix 'ag' to all fields
ag_attrs = ['edge_index', 'x']
if antigen is not None:
for ag_attr in ag_attrs:
setattr(self, f'ag_{ag_attr}', getattr(antigen, ag_attr))
# antibody: add prefix 'ab' to all fields
ab_attrs = ['edge_index', 'x']
if antibody is not None:
for ab_attr in ab_attrs:
setattr(self, f'ab_{ab_attr}', getattr(antibody, ab_attr))
# incremental operation: for minibatching
# the index incremental follows # of nodes of antibody or antigen
def __inc__(self, key, value, *args, **kwargs):
if key == 'ag_edge_index': return self.ag_x.shape[0]
elif key == 'ab_edge_index': return self.ab_x.shape[0]
else: return super().__inc__(key, value, *args, **kwargs)
Now given a list of AbAgPair objects, we can build the data loader with antigen-antibody pairs.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.model_selection import train_test_split
from torch_geometric.loader import DataLoader
datalist = []
for pairname in tqdm(pairnames[:n], desc='Loading Ab-Ag Pairs'):
g_ag, g_ab = ..., ... # the graphs for pairing
paired_data = AbAgPair(g_ag, g_ab)
datalist.append(paired_data)
# train and test splitting
train_data, test_data = train_test_split(datalist, test_size=0.2, random_state=random_state)
# dataloaders:
# Need to keep track of the batch index for both antibody and antigen separately
# The batched data will contain additional fields: 'ag_x_batch' and 'ab_x_batch'
train_dataloader = DataLoader(train_data, batch_size=batch_size, shuffle=True, follow_batch=['ag_x', 'ab_x'])
test_dataloader = DataLoader(test_data, batch_size=batch_size, shuffle=True, follow_batch=['ag_x', 'ab_x'])
2. Model: EPI-EPMP
Now the data and loader is constructed. The model is built based on how it was architected in the figure above.
2.1 Model Architecture
The model needs to process information differently for ab_ and ag_.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import torch
from torch_geometric.nn import GATConv, GCNConv, Linear
from torch.nn import Sequential, Tanh, BatchNorm1d
# EPI-EPMP Multitasking Model
class EpiEPMP(torch.nn.Module):
def __init__(self, node_attr_dim, edge_attr_dim, hidden_dim, h1_dim, h2_dim, share_weight=False, dropout=0.2, heads=4):
super(EpiEPMP, self).__init__()
self.node_attr_dim = node_attr_dim
self.edge_attr_dim = edge_attr_dim
self.hidden_dim = hidden_dim
self.h1_dim = h1_dim # dim after the first gnn
self.h2_dim = h2_dim # dim after the bipartite message passing
self.share_weight = share_weight # Should model weights be shared between Ag and Ab?
self.dropout = dropout
self.heads = heads
# 2 layers antigen GCN (2-hop basically)
self.ag_gnn1 = GCNConv(self.node_attr_dim, self.hidden_dim)
self.ag_gnn2 = GCNConv(self.hidden_dim, self.h1_dim)
if self.share_weight:
# if weights are shared, 2 layers of antibody GCN are identical with antigen GCN
self.ab_gnn1 = self.ag_gnn1
self.ab_gnn2 = self.ag_gnn2
else:
# or the antibody uses new GCNs
self.ab_gnn1 = GCNConv(self.node_attr_dim, self.hidden_dim)
self.ab_gnn2 = GCNConv(self.hidden_dim, self.h1_dim)
self.ag_bnorm1 = BatchNorm1d(self.hidden_dim)
self.ag_bnorm2 = BatchNorm1d(self.h1_dim)
self.ab_bnorm1 = BatchNorm1d(self.hidden_dim)
self.ab_bnorm2 = BatchNorm1d(self.h1_dim)
# The GATs for the bipartite graph
self.bp_gnn1 = GATConv(self.h1_dim, self.hidden_dim, heads=self.heads, concat=True, dropout=self.dropout)
self.bp_gnn2 = GATConv(self.hidden_dim * self.heads, self.h2_dim, heads=self.heads, concat=False, dropout=self.dropout)
# antigen prediction head
self.ag_classifier = Sequential(Linear(self.h1_dim + self.h2_dim, self.hidden_dim),
Tanh(),
Linear(self.hidden_dim, 1))
# Classifier can be shared or not
# The same as the GCN's
if self.share_weight:
self.ab_classifier = self.ag_classifier
else:
self.ab_classifier = Sequential(Linear(self.h1_dim + self.h2_dim, self.hidden_dim),
Tanh(),
Linear(self.hidden_dim, 1))
def forward(self, ag_x, ag_edge_index, ag_x_batch, \
ab_x, ab_edge_index, ab_x_batch):
# antigen gnn + batchnorm
ag_h1 = self.ag_bnorm1(torch.tanh(self.ag_gnn1(ag_x, ag_edge_index)))
ag_h1 = self.ag_bnorm2(torch.tanh(self.ag_gnn2(ag_h1, ag_edge_index)))
# antibody gnn + batchnorm
ab_h1 = self.ab_bnorm1(torch.tanh(self.ab_gnn1(ab_x, ab_edge_index)))
ab_h1 = self.ab_bnorm2(torch.tanh(self.ab_gnn2(ab_h1, ab_edge_index)))
# bipartite construction
x, edge_index, ag_index, ab_index = bipartite(ag_h1, ag_x_batch, ab_h1, ab_x_batch)
h2 = torch.tanh(self.bp_gnn1(x, edge_index))
h2 = torch.tanh(self.bp_gnn2(h2, edge_index))
ag_h2, ab_h2 = h2[ag_index], h2[ab_index]
# concat skip connection and clasifier heads
ag_out = self.ag_classifier(torch.cat([ag_h1, ag_h2], dim=1))
ab_out = self.ab_classifier(torch.cat([ab_h1, ab_h2], dim=1))
return ag_out, ag_h1, ag_h2, ab_out, ab_h1, ab_h2
2.2 The Bipartite Graph
The bipartite graph is constructed in such way that every antigen node has edges connecting to all antibody nodes and vise versa. The antigen/antibody nodes themselves don’t necessarily need to be fully connected in the bipartite because such locality was captured in the original protein graph already. In the bipartite, we just want the model to pass messages between antigen and antibody.
The bipartite is built with the minibatched paired data, i.e. batch_size bipartites are built for each minibatch, so ag_x_batch and ab_x_batch are used to keep track which bipartite is which.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import torch
from torch_geometric.utils import add_self_loops
# create bipartite using index and attributes
# with device consistent tensors
def bipartite(ag_x, ag_x_batch, ab_x, ab_x_batch):
assert ag_x.device == ag_x_batch.device == ab_x.device == ab_x_batch.device
device = ag_x.device
# node attr and edge index
x, edge_index = torch.tensor([], dtype=torch.float, device=device), torch.tensor([], dtype=torch.long, device=device)
# antigen and antibody index for later retreval of the matrix
ag_index, ab_index = torch.tensor([], dtype=torch.long, device=device), torch.tensor([], dtype=torch.long, device=device)
# getting the unique batch index for the antibody and antigens
ag_batch_unique, ab_batch_unique = ag_x_batch.unique(), ab_x_batch.unique()
assert ab_batch_unique.shape[0] == ag_batch_unique.shape[0]
# creating the bipartite following the batch index
for b in ag_batch_unique:
idx_ag, idx_ab = torch.eq(ag_x_batch, b), torch.eq(ab_x_batch, b)
n_ag, n_ab = idx_ag.sum(), idx_ab.sum()
# keeping the offset
offset = x.shape[0]
# antigen
ag = torch.tensor(range(offset, offset + n_ag), dtype=torch.long, device=device)
ag_index = torch.cat([ag_index, ag])
# antibody
ab = torch.tensor(range(offset + n_ag, offset + n_ag + n_ab), dtype=torch.long, device=device)
ab_index = torch.cat([ab_index, ab])
# construct the edge_index
edge_index = torch.cat([edge_index, torch.cat([ag.repeat_interleave(n_ab).view(1, -1), ab.repeat(n_ag).view(1, -1)], dim=0)], dim=1)
edge_index = add_self_loops(edge_index)[0]
# construct the node feature
x = torch.cat([x, ag_x[idx_ag], ab_x[idx_ab]], dim=0)
return x, edge_index, ag_index, ab_index
3. In-Batch Sampling
Since paratope and epitope residues are generally less than 10 \% of the number of residues (nodes) in the protein (graph). One can scale the loss function to account for the label imbalance. I chose to do the balance sampling while leaving equal weighting of the paratope and epitope prediction losses. The in-batch sampling function is as follows.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import torch
import numpy as np
def sample_balanced_indices(y):
pos_ix = torch.nonzero(y).view(-1).cpu()
n_pos = pos_ix.shape[0]
neg_indices = torch.nonzero(y != 1).view(-1)
neg_ix = torch.tensor(np.random.choice(neg_indices.cpu().numpy(), min(n_pos, neg_indices.shape[0]), replace=False))
return torch.cat((pos_ix, neg_ix))
# For each batch index, sample balanced labels of the negative (non-epitope) nodes
def in_batch_sampling(y, batch):
ubatch = batch.unique()
idx, sampled_batch = torch.tensor([], dtype=torch.long), torch.tensor([], dtype=torch.long)
offset = 0 # keeping track of the # of nodes as offset for different batch index
for b in ubatch:
yb = y[batch == b]
ix = sample_balanced_indices(yb) + offset
idx = torch.cat([idx, ix])
offset += yb.shape[0]
return idx, sampled_batch
4. Observations and Discussions
4.1 From the Paper
The authors demonstrated good validation case with the SARS-COV-2 spike protein and a corresponding antibody that targets it.
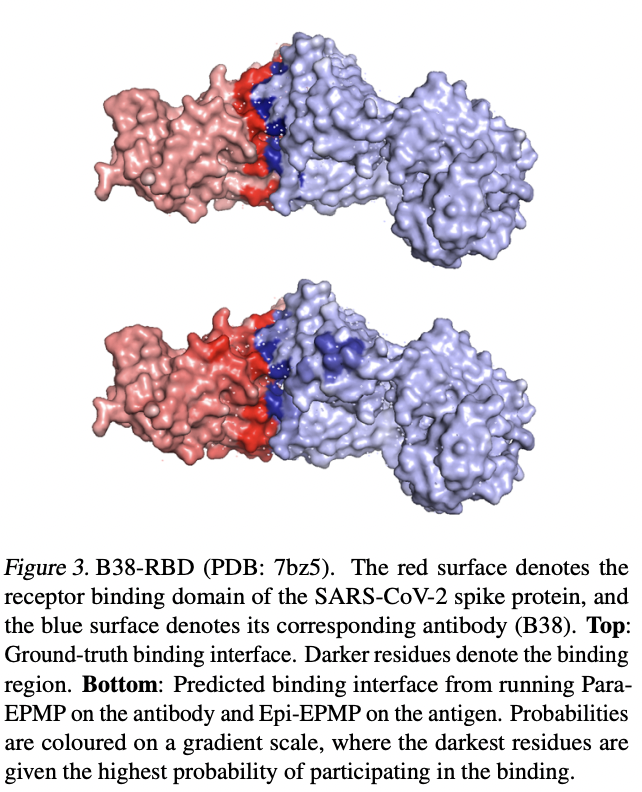
4.2 Performances
I experiemnted with self-generated structural features, i.e. ag_x and ab_x and achieved similar performances as reported in the paper.
For antibody paratopes: AUROC = 0.800 (0.966), AUPRC = 0.551 (0.752). The bracketed values were the reported values. The discrepancy is that the authors only use the CDRs regions to feed into the model where as I was using the whole antibody, including the framework regions, which makes the paratope task a bit challenging as the labels are much more imbalanced and noises or confusions might arise from the loop regions on top of the CDR loops. However, genrally, antibody CDRs can be determined purely from sequences, so there is so surprise that the paratopes are easier to predict (middle of the CDR loops of H3 and L3). The left figure below is the predicted paratopes among different anibody fabs.

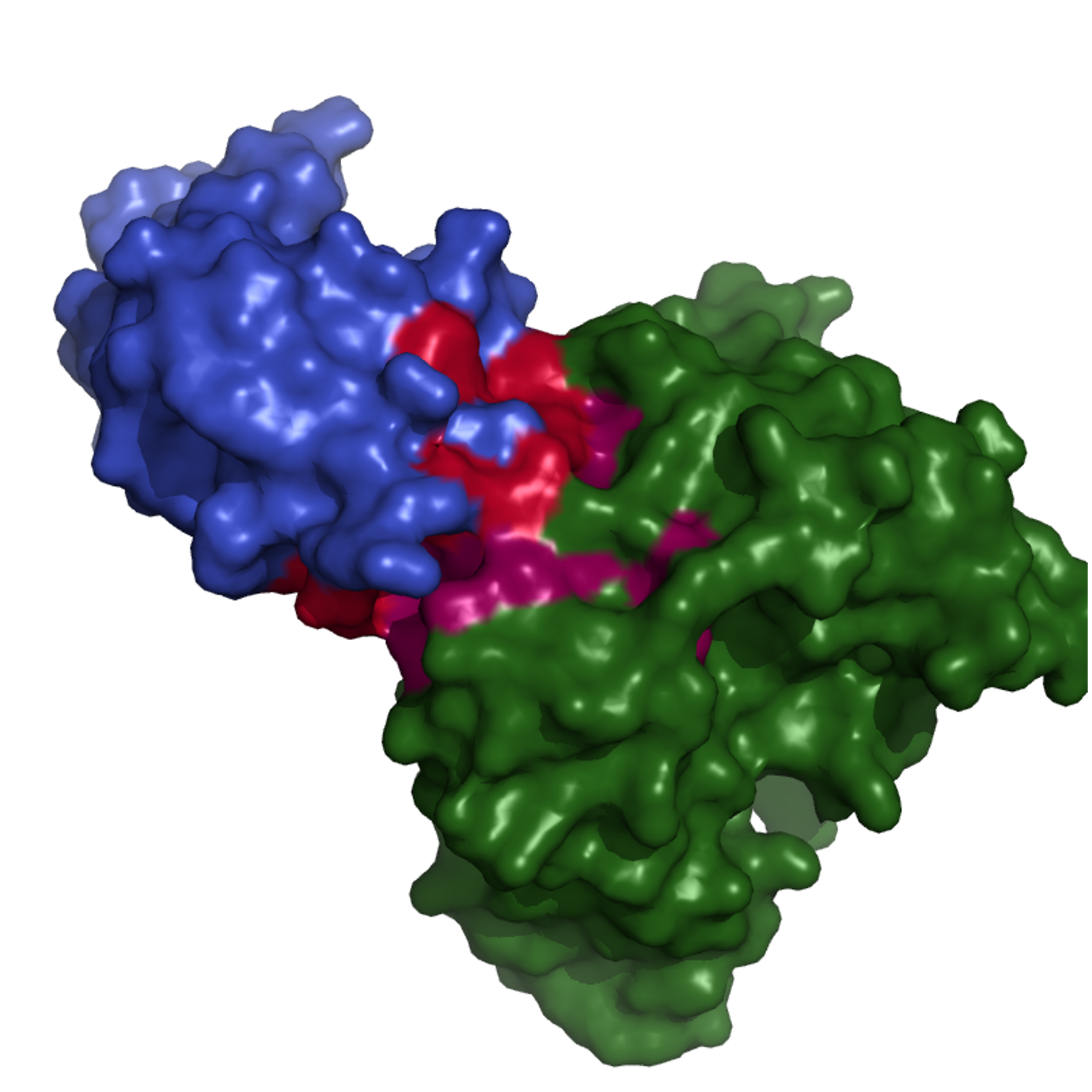
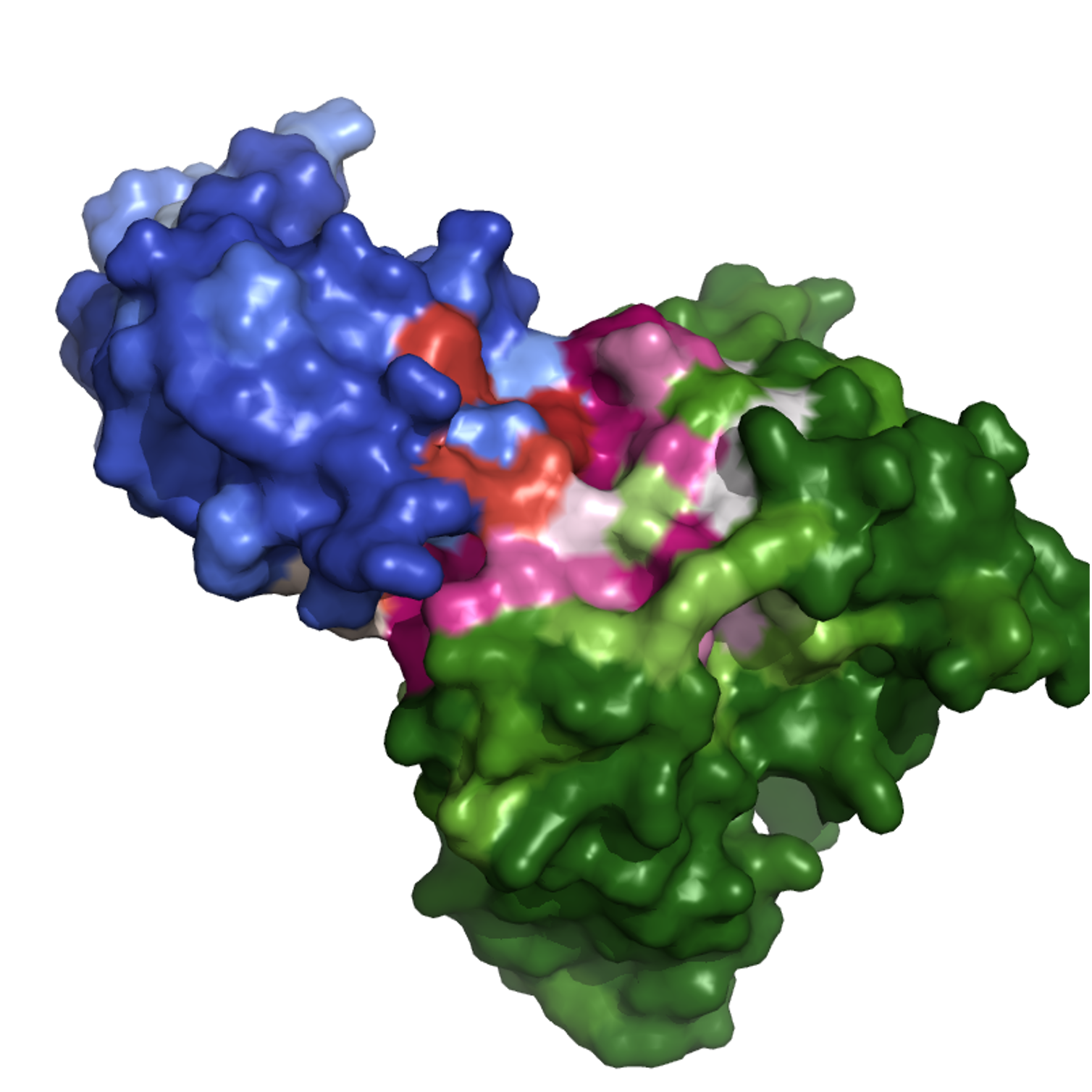
For antigen epitopes: AUROC = 0.798 (0.710), AUPRC = 0.319 (0.277). The middle figure is the ground truth and right is the model prediction of one sample in the testing set with anitgen and antibody shown in blue and green with different probabilities overlayed on the surfaces using PyMol.
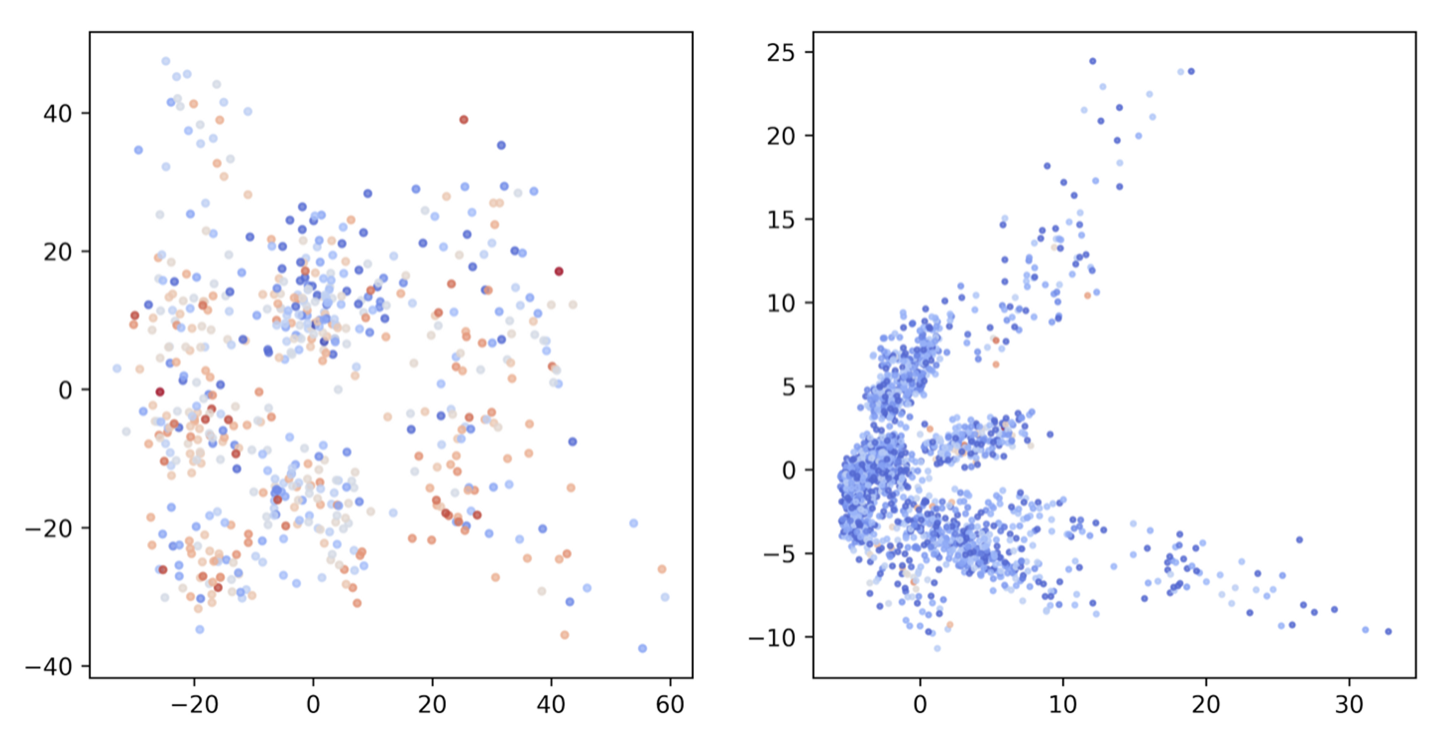
It is usually interesting to look under the hood what the model learned. Here are the PCA plots for antigen and antibody node embeddings (ag_h1 and ab_h1) colored by the node degree. There is no obvious correlation between embeddings and node degree because the model was trained in such way that it focused on structural context, i.e. node features while still taking local neighborhood into account.
4.3 Efficiency
Generally, the training took about 48 GPU-hrs for a few k of data and epochs. The inference took ~ 2s. The computationally expensive part was the featurization.
The minibatch might bags LARGE antigens with >500 residues, and might consume large memory or even cause RuntimeError: CUDA error: out of memory.
4.4 Some Thoughts
When the antibody and antigen complex is formed for cryoEM or X-ray cystallography, the conformations of both changed. The side chains might pertrude and all the structural context might differ from the original free antibody or antigen. Using the bound complex to predict the interfaces or epitopes might suffer information leakage that undermine the model’s generalizability to free antigens for antibody designs or applications.
This EPI-EPMP model is not a conditional model. It does message passing between antigen and antibodies but the authors did not show that if the model learned the conditional probability P(epiotpe | paratope) or independent probabilities P(epitope) P(paratope). I was convinced that the latter was the case, meaning that if one pairs any antibody to the same antigen, the epitope prediction does not vary, which might limit the real-world use case as people care more about where different antibodies bind to a certain target. A deeper look into the GAT attentional weight in the bipartite confirms that the attentional edges (or soft edges) are very sparse, i.e. the model might as well use an epitope node embedding ONLY rather than paying attention to ANY antibody nodes. I call this as attention collapse, where the dense attentional edges collaped to self-attention after training.
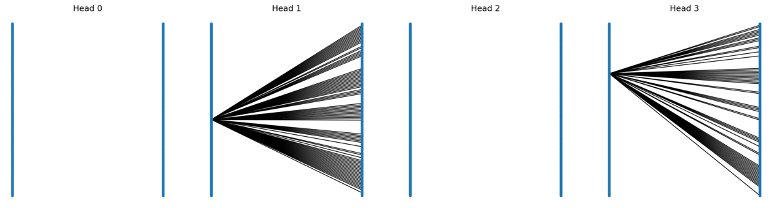
One solution to this could be forcing information flow into the epitope prediction.
Sometimes the epitopes span a large portion on the antigen surface; further narrowing down of the epitopes might require force-field (physical) modeling of the docking free energies but at least the model has ruled out quite a large set of potential patches.
Here is the repo of my implementation of the EPI-EPMP multitasking model.
Reference
- Alice Del Vecchio, Andreea Deac, Pietro Liò, Petar Veličković, Neural message passing for joint paratope-epitope prediction, https://arxiv.org/abs/2106.00757