After playing with e3nn and a toy example with the tetris shape classification, I am going to move from the invariant model to equivariant model, which outputs type-1 (\(l=1\)) feature like 3D coordinates or even higher order tensors. This example is to predict the trajectories of the many-body dynamics, which is adopted from the dmol book Ch. 19.

2. Trajectory Prediction

Given a position snapshot of a connected 12-body system at time \(t\), \(x(t)\), predict the positions of each particle at \(t+\Delta t\), i.e. \(x(t+\Delta t)\).

The data can be found here

Let’s first take a look at the first frame, the second frame and later frames:

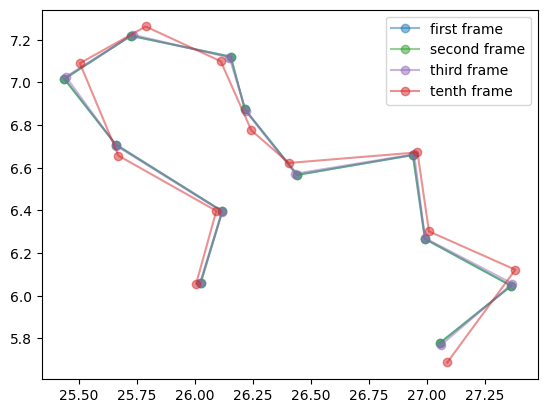
Given a snapshot, our equivariant model can be trained to predict the coordinates of the next frame \(x(t+\Delta t)\) or the displacement \(\Delta x = x(t + \Delta t) - x(t)\). These two objectives might have different 3D distributions. The later turns out to be easier to model and we will focus on predicting the delta.

2.1 Packages

Here we load the required packages and set up global parameters:

# imports 
import torch, e3nn, urllib, einops

import numpy as np 
import torch_geometric as pyg
import matplotlib.pyplot as plt

from torch_cluster import radius_graph
from torch_geometric.data import Data
from torch_geometric.loader import DataLoader
from torch_geometric.nn import GATConv
from torch_scatter import scatter

from tqdm.auto import tqdm
from sklearn.metrics import r2_score
import scipy.spatial.transform as trans

from e3nn import o3
from e3nn.o3 import FullyConnectedTensorProduct
from e3nn.nn.models.gate_points_2101 import Network

if torch.cuda.is_available(): DEVICE = torch.device('cuda')
else: DEVICE = torch.device('mps') if torch.backends.mps.is_available() else torch.device('cpu')
print(f'Using device: {DEVICE}')

Note that there are few functions in torch_geometric that are not compatible with Apple’s M1/M2 GPU, so if one is using mps, e3nn or functionalities in torch_geometric might raise low-level errors.

2.2 Data

# Retrieving data from trajectory

urllib.request.urlretrieve("https://github.com/whitead/dmol-book/raw/main/data/paths.npz", "paths.npz")
paths = np.load('paths.npz')['arr']

print('path shape = ', paths.shape) # time stamp, particle, xy

plt.plot(paths[0, :, 0], paths[0, :, 1], 'o-', color='tab:blue', label='first frame', alpha=0.5)
plt.plot(paths[1, :, 0], paths[1, :, 1], 'o-', color='tab:green', label='second frame', alpha=0.5)
plt.plot(paths[2, :, 0], paths[2, :, 1], 'o-', color='tab:purple', label='third frame', alpha=0.5)
plt.plot(paths[9, :, 0], paths[9, :, 1], 'o-', color='tab:red', label='tenth frame', alpha=0.5)
plt.legend()
plt.show()

path shape = (2048, 12, 2)

The path contains 2048 frames of 2D coordinates for 12 particles. The output plot was shown above.

The data is the \(x(t)\) and the label is either \(x(t + \Delta t)\) or \(\Delta x\). We will arrange the path accordingly. Additionally, we will prepare the data with and without shuffling the data.

# Process the data into datasets and dataloaders
def build_dataset(x, y): 
    data = []
    for frame, label in zip(x, y):
        data.append(pyg.data.Data(x=None, pos=frame.to(torch.float32), y=label.to(torch.float32)))
    return data

# make 3d trajectories
nt, npoint, __ = paths.shape
traj = np.concatenate((paths, np.zeros((nt, npoint, 1))), axis=-1)

# two types of data:
# 1. feature = x(t), label = x(t+1), prediction = label
# 2. feature = x(t), label = dx(t), prediction = x(t+1) = x(t) + dx(t)
features, labels = torch.from_numpy(traj[:-1]).to(torch.float), torch.from_numpy(traj[1:]).to(torch.float)
dx = labels - features

# training = 0:n, testing = n:2048, n = 1637
n = 1637
pos_prediction_train_dataset = build_dataset(features[:n], labels[:n])
pos_prediction_test_dataset = build_dataset(features[n:], labels[n:])

dx_prediction_train_dataset = build_dataset(features[:n], dx[:n])
dx_prediction_test_dataset = build_dataset(features[n:], dx[n:])

# data loaders: [pos, dx] x [shuffle or not] x [train, test]
BATCH_SIZE = 32
dataloaders = dict({'pos': dict(), 'dx': dict()})

dataloaders['pos']['no_shuffle'] = dict({'train': DataLoader(pos_prediction_train_dataset, batch_size=BATCH_SIZE, shuffle=False), 
                                         'test': DataLoader(pos_prediction_test_dataset, batch_size=BATCH_SIZE, shuffle=False)})
dataloaders['pos']['shuffle'] = dict({'train': DataLoader(pos_prediction_train_dataset, batch_size=BATCH_SIZE, shuffle=True), 
                                      'test': DataLoader(pos_prediction_test_dataset, batch_size=BATCH_SIZE, shuffle=True)})

dataloaders['dx']['no_shuffle'] = dict({'train': DataLoader(dx_prediction_train_dataset, batch_size=BATCH_SIZE, shuffle=False), 
                                        'test': DataLoader(dx_prediction_test_dataset, batch_size=BATCH_SIZE, shuffle=False)})
dataloaders['dx']['shuffle'] = dict({'train': DataLoader(dx_prediction_train_dataset, batch_size=BATCH_SIZE, shuffle=True), 
                                     'test': DataLoader(dx_prediction_test_dataset, batch_size=BATCH_SIZE, shuffle=True)})

Take a look at what the minibatch is like:

print(len(dataloaders['pos']['no_shuffle']['train'])) # 52
batch_data = next(iter(dataloaders['pos']['no_shuffle']['train']))
print(batch_data)
# DataBatch(y=[384, 3], pos=[384, 3], batch=[384], ptr=[33])

assert torch.allclose(batch_data.pos[12:], batch_data.y[:-12])

2.3 Baseline Models

With the dataloaders at hand, we can start to build the models. First, we will construct 2 baseline models for comparisons. The first one is just the normal MLP and the second one is the GNN baseline using the equivariant features (to make it comparable with models later).

# Baseline models: 
# 1. Just a MLP
# 2. GNN baseline

# input = a set of 12 coordinates
# output = a set of 12 coordinates

loss_fn = torch.nn.MSELoss()


class MLPBaseline(torch.nn.Module):

    def __init__(self, hidden_dim=64): 
        super(MLPBaseline, self).__init__()
        self.dim = 36
        self.hidden_dim = hidden_dim
        self.mlp = torch.nn.Sequential(torch.nn.Linear(self.dim, self.hidden_dim),
                                       torch.nn.Linear(self.hidden_dim, self.hidden_dim),
                                       torch.nn.Linear(self.hidden_dim, self.dim))
        
    def forward(self, data): 
        pos = einops.rearrange(data.pos, '(t p) c -> t (p c)', p=12)
        pos = self.mlp(pos)
        pos = einops.rearrange(pos, 't (p c) -> (t p) c', p=12)
        return pos

   
# Using spherical harmonics as featurizer
class GNNBaseline(torch.nn.Module): 

    def __init__(self, dim_in=16, edge_dim=16, hidden_dim=256, dim_out=3, heads=4): 
        super(GNNBaseline, self).__init__()
        self.dim_in = dim_in
        self.edge_dim = edge_dim
        self.hidden_dim = hidden_dim
        self.dim_out = dim_out
        self.heads = heads

        self.irreps_sh = o3.Irreps.spherical_harmonics(3)
        
        self.gat1 = GATConv(dim_in, hidden_dim, edge_dim=edge_dim, heads=heads)
        self.gat2 = GATConv(hidden_dim * heads, hidden_dim, edge_dim=edge_dim, heads=heads)
        self.head = torch.nn.Sequential(torch.nn.Linear(hidden_dim * heads, hidden_dim),
                                        torch.nn.GELU(),
                                        torch.nn.Linear(hidden_dim, dim_out))
        
    def forward(self, data):

        num_neighbors = 6
        num_nodes = 12
        
        # tensors of indices representing the graph, using fully connected
        edge_index = radius_graph(x=data.pos, r=2.5, batch=data.batch)
        edge_src, edge_dst = edge_index
        edge_vec = data.pos[edge_src] - data.pos[edge_dst]
        
        edge_features = o3.spherical_harmonics(l=self.irreps_sh, x=edge_vec, normalize=False, normalization='component')
        node_features = scatter(edge_features, edge_dst, dim=0).div(num_neighbors**0.5)

        # GNN message passing
        x = self.gat1(node_features, edge_index, edge_attr=edge_features)
        x = self.gat2(x, edge_index, edge_attr=edge_features)
        
        return self.head(x)

Let’s try to feed in one minibatch.

mlpbase = MLPBaseline()
pred = mlpbase(batch_data)
print(pred.shape) # torch.Size([384, 3])
print(loss_fn(pred, batch_data.y)) # tensor(253.8258, grad_fn=<MseLossBackward0>)

gnnbase = GNNBaseline()
pred = gnnbase(batch_data)
print(pred.shape) # torch.Size([384, 3])
print(loss_fn(pred, batch_data.y)) # tensor(244.7130, grad_fn=<MseLossBackward0>)

We need some helper functions for model training, evaluations and visualizations. These functions are straightforward.

# general training function 
EPOCHS = 100
LR = 1e-3

def train(model, trainloader, testloader, epochs=EPOCHS, lr=LR, device=DEVICE, opt='Adam'): 

    model.to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=lr) if opt == 'Adam' else torch.optim.AdamW(model.parameters(), lr=lr)
    loss_fn = torch.nn.MSELoss()

    every_n = epochs // 100
    logs = dict({'train_loss': np.zeros(epochs + 1), 'test_loss': np.zeros(epochs + 1)})
    pbar = tqdm(range(epochs + 1))
    for step in pbar: 
        
        train_loss, test_loss = [], []

        # training: 
        model.train()
        for data in trainloader: 
            data = data.to(device)
            pred = model(data)
            loss = loss_fn(pred, data.y)

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            train_loss.append(loss.item())
        
        logs['train_loss'][step] = np.array(train_loss).mean()

        # testing: 
        model.eval()
        with torch.no_grad():
            for data in testloader: 
                data = data.to(device)
                pred = model(data)
                loss = loss_fn(pred, data.y)
                test_loss.append(loss.item())
        
        logs['test_loss'][step] = np.array(test_loss).mean()

        trainl, testl = logs['train_loss'][step], logs['test_loss'][step]
        s = f'epoch {step:5d} | Train MSE {trainl:<10.5f} | Test MSE {testl:<10.5f}'
        if step % every_n == 0: pbar.set_description(s)
    
    return model, logs


# get forward pass for all testing set 
def forward_pass(model, dataset, delta=False): 
    model.eval()
    device = next(model.parameters()).device
    pbar = tqdm(dataset)
    with torch.no_grad():
        if delta: 
            pred = [(data.pos.to(device) + model(data.to(device))).unsqueeze(0) for data in pbar]
            truth = [(data.pos + data.y).unsqueeze(0) for data in pbar]
        else: 
            pred = [model(data.to(device)).unsqueeze(0) for data in pbar]
            truth = [data.y.unsqueeze(0) for data in dataset]
    return torch.concat(pred, dim=0).cpu(), torch.concat(truth, dim=0).cpu()


# show correlations of center of mass, first particle center of mass, 7th particle x coord, last particle y coord
def show_correlation(y_hat, y): 
    assert y_hat.shape == y.shape
    y_hat_cm, y_cm = y_hat.mean(-1), y.mean(-1)
    y_hat_cmm, y_cmm = y_hat.mean((-2, -1)), y.mean((-2, -1))

    fig, axes = plt.subplots(1, 4, figsize=(20, 5))
    axes[0].plot(y_cmm, y_cmm, '-', color='black')
    axes[0].plot(y_cmm, y_hat_cmm, '.')
    axes[0].set_title(f'COM, rsq = {r2_score(y_cmm, y_hat_cmm): .3f}')

    axes[1].plot(y_cm[:, 0], y_cm[:, 0], '-', color='black')
    axes[1].plot(y_cm[:, 0], y_hat_cm[:, 0], '.')
    axes[1].set_title(f'First COM, rsq = {r2_score(y_cm[:, 0], y_hat_cm[:, 0]): .3f}')

    axes[2].plot(y[:, 6, 0], y[:, 6, 0], '-', color='black')
    axes[2].plot(y[:, 6, 0], y_hat[:, 6, 0], '.')
    axes[2].set_title(f'7th x, rsq = {r2_score(y[:, 6, 0], y_hat[:, 6, 0]): .3f}')

    axes[3].plot(y[:, -1, 1], y[:, -1, 1], '-', color='black')
    axes[3].plot(y[:, -1, 1], y_hat[:, -1, 1], '.')
    axes[3].set_title(f'last y, rsq = {r2_score(y[:, -1, 1], y_hat[:, -1, 1]): .3f}')

    plt.show()


# show and compare trajectories
def compare_trajectories(y_hat, y, interval=25): 
    assert y_hat.shape == y.shape
    nt = y.shape[0]
    fig, axes = plt.subplots(1, 2, squeeze=True, figsize=(16, 4))

    axes[0].set_title("Trajectory")
    axes[1].set_title("Predicted Trajectory")

    cmap = plt.get_cmap("coolwarm")
    for i in range(0, nt, interval):
        axes[0].plot(y[i, :, 0], y[i, :, 1], ".-", alpha=0.2, color=cmap(i / nt))
        axes[1].plot(y_hat[i, :, 0], y_hat[i, :, 1], ".-", alpha=0.2, color=cmap(i / nt))
    for i in range(2):
        axes[i].set_xticks([])
        axes[i].set_yticks([])

    plt.show()

For each model, we will train it, evaluate the trained model using testing data and visualize the testing trajectories. For evaluation, we select correlations of center of mass, first particle center of mass, 7th particle x coordinate, last particle y coordinate. Therefore, we will be able to see the small variations in a more granular way.

# test training 

epochs = 1000
mlpbase, mlpbase_logs = train(MLPBaseline(), dataloaders['dx']['no_shuffle']['train'], dataloaders['dx']['no_shuffle']['test'], epochs=epochs)
gnnbase, gnnbase_logs = train(GNNBaseline(), dataloaders['dx']['no_shuffle']['train'], dataloaders['dx']['no_shuffle']['test'], epochs=epochs)

mlp_y_hat, y = forward_pass(mlpbase, dx_prediction_test_dataset, delta=True)
show_correlation(mlp_y_hat, y)
compare_trajectories(mlp_y_hat, y)

gnn_y_hat, y2 = forward_pass(gnnbase, dx_prediction_test_dataset, delta=True)
assert torch.allclose(y, y2)
show_correlation(gnn_y_hat, y)
compare_trajectories(gnn_y_hat, y)

epoch  1000 | Train MSE 0.00003    | Test MSE 0.00003   : 100%|██████████| 1001/1001 [01:31<00:00, 10.90it/s]
epoch  1000 | Train MSE 0.00002    | Test MSE 0.00003   : 100%|██████████| 1001/1001 [05:21<00:00,  3.11it/s]
100%|██████████| 410/410 [00:00<00:00, 5012.90it/s]
100%|██████████| 410/410 [00:01<00:00, 393.63it/s]

For MLP no shuffle:

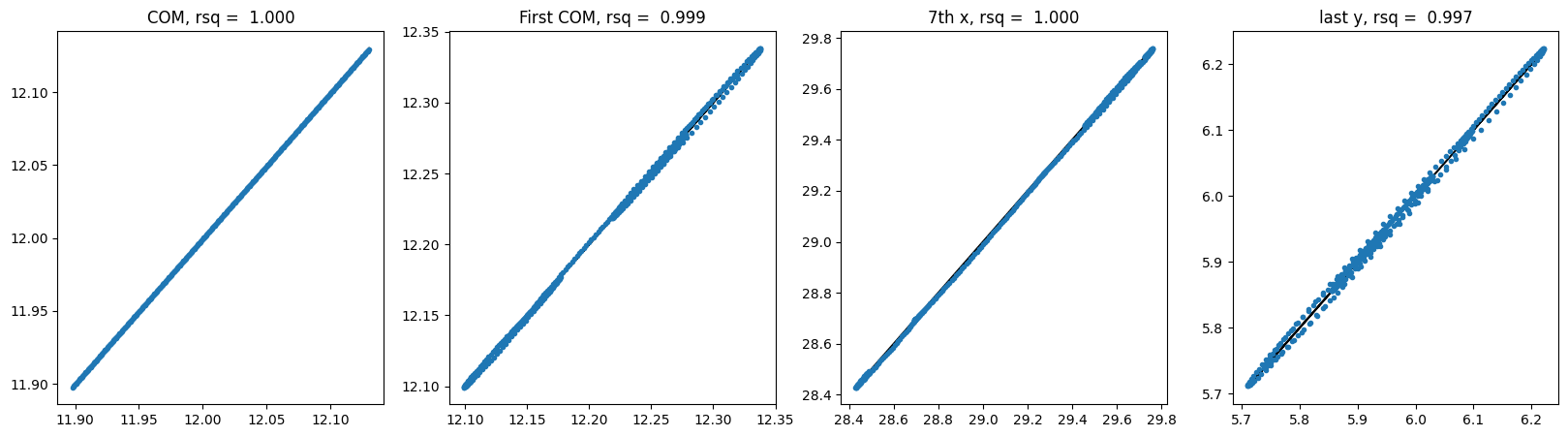
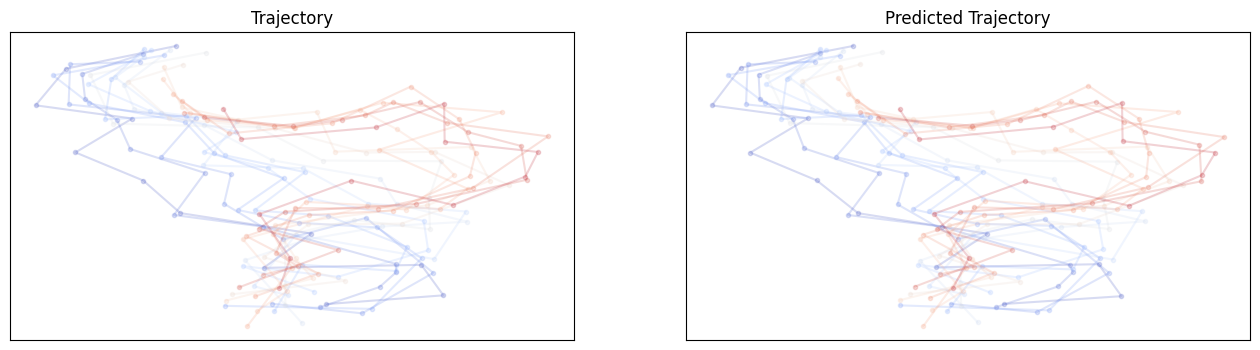
For GNN no shuffle:

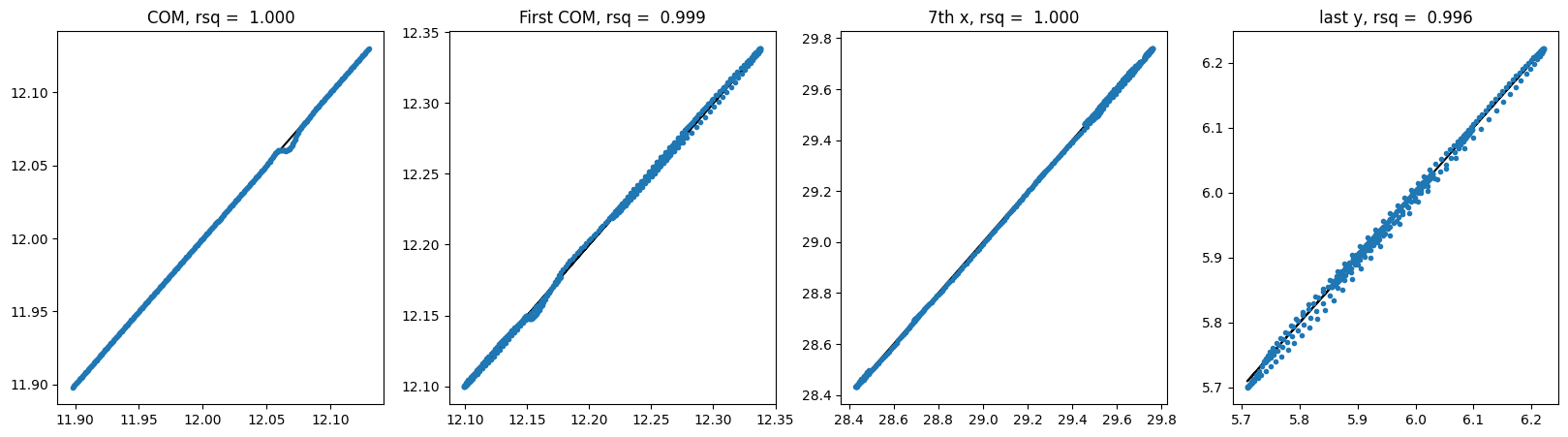
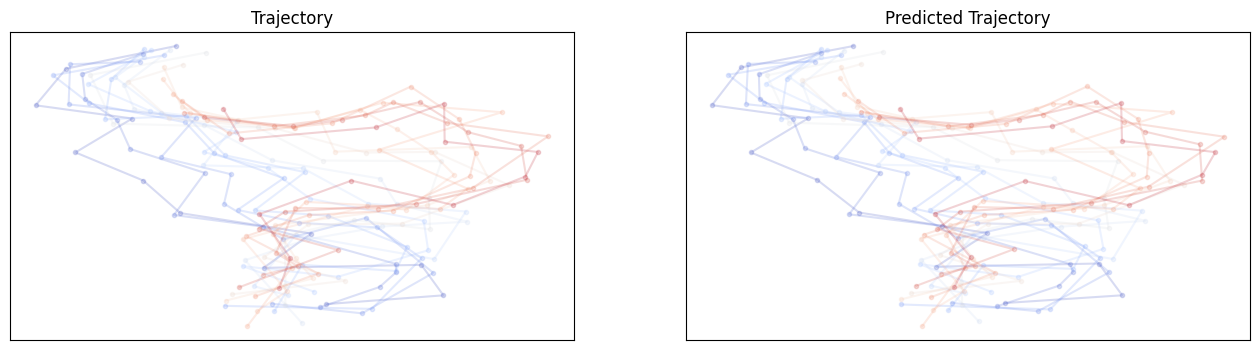
The baseline models have already good performances, which might be coming from the ordering of the data. Let’s try it again with shuffled dataloader.

epochs = 1000
mlpbase_sh, mlpbase_sh_logs = train(MLPBaseline(), dataloaders['dx']['shuffle']['train'], dataloaders['dx']['shuffle']['test'], epochs=epochs)
gnnbase_sh, gnnbase_sh_logs = train(GNNBaseline(), dataloaders['dx']['shuffle']['train'], dataloaders['dx']['shuffle']['test'], epochs=epochs)

mlp_y_hat, y = forward_pass(mlpbase_sh, dx_prediction_test_dataset, delta=True)
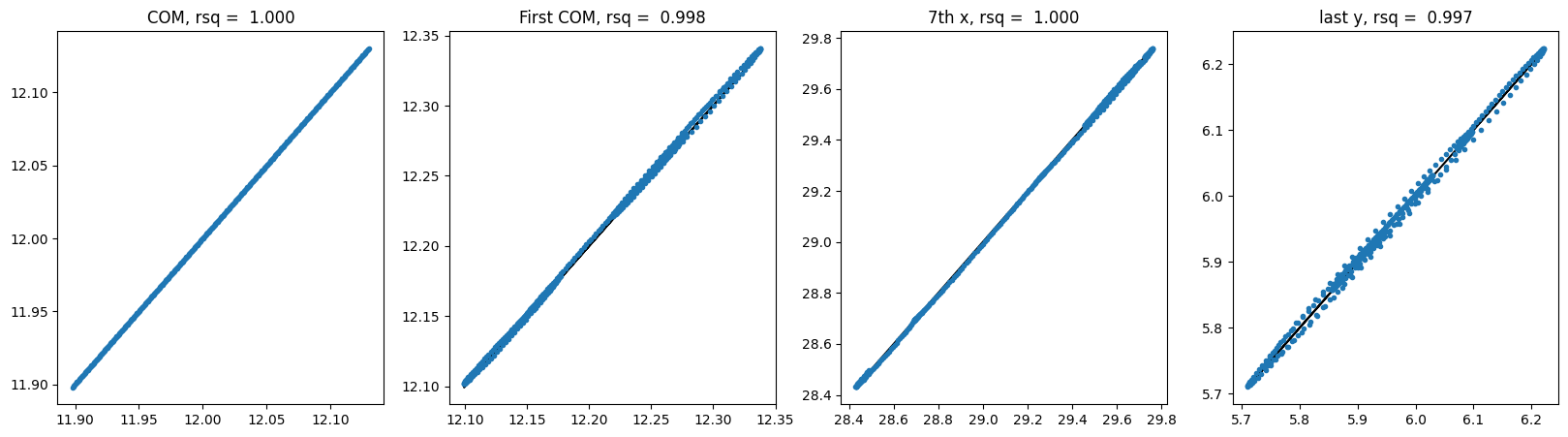
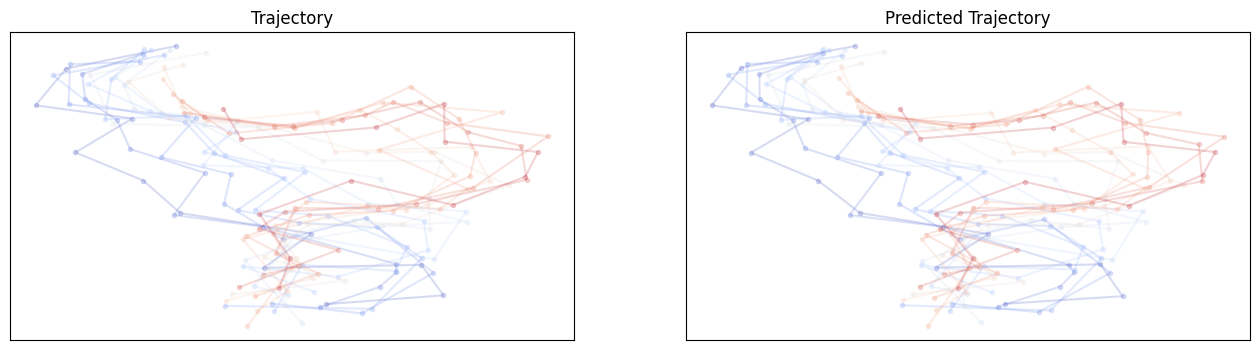
show_correlation(mlp_y_hat, y)
compare_trajectories(mlp_y_hat, y)

gnn_y_hat, y2 = forward_pass(gnnbase_sh, dx_prediction_test_dataset, delta=True)
assert torch.allclose(y, y2)
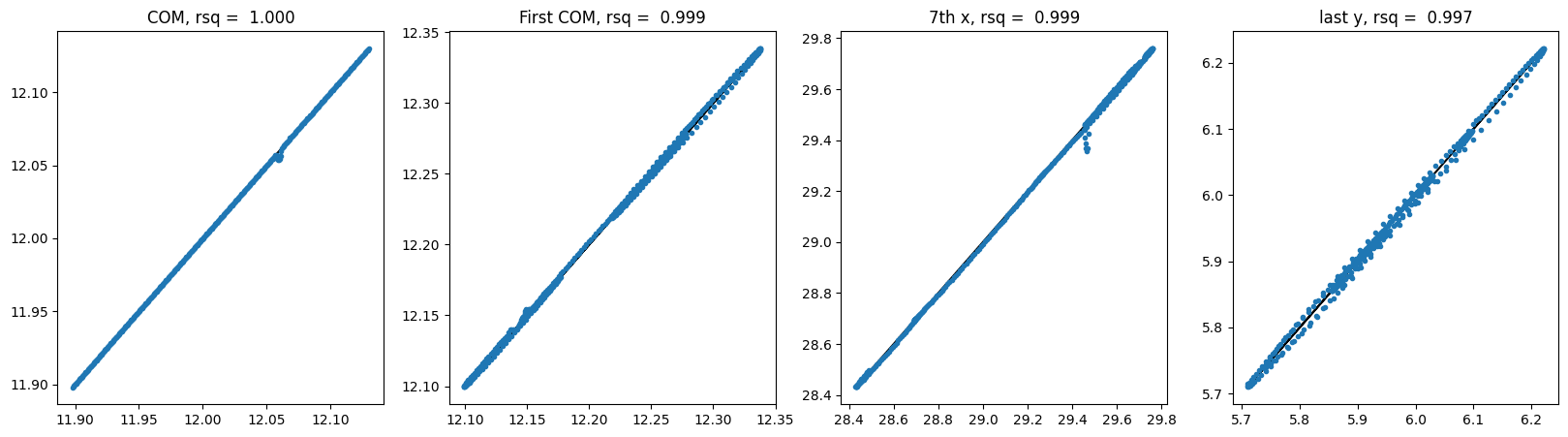
show_correlation(gnn_y_hat, y)
compare_trajectories(gnn_y_hat, y)

epoch  1000 | Train MSE 0.00002    | Test MSE 0.00004   : 100%|██████████| 1001/1001 [01:35<00:00, 10.48it/s]
epoch  1000 | Train MSE 0.00002    | Test MSE 0.00003   : 100%|██████████| 1001/1001 [05:34<00:00,  2.99it/s]
100%|██████████| 410/410 [00:00<00:00, 7180.50it/s]
100%|██████████| 410/410 [00:01<00:00, 389.29it/s]

For MLP shuffle:

For GNN shuffle:

2.4 E3NN Models

Let’s try to build the equivariant model from e3nn and see if the models can achieve better predictions.

We will recycle the model from the Tetris example except the final aggregation operation for the e3nn_small model. Similarly, we recycle the Network as the e3nn_large model. Explicitly:

# E3NN
class EquivariantPolynomial(torch.nn.Module):

    def __init__(self, r=3.5):
        super(EquivariantPolynomial, self).__init__()
        self.r = r
        self.irreps_sh = o3.Irreps.spherical_harmonics(3) 
        irreps_mid = o3.Irreps('8x0e + 8x0o + 16x1e + 16x1o + 8x2e + 8x2o') # add l = 3 to the hidden irreps
        irreps_out = o3.Irreps('1x1o') # each particle outputs a vector (1x1o)

        self.tp1 = FullyConnectedTensorProduct(irreps_in1=self.irreps_sh, 
                                               irreps_in2=self.irreps_sh,
                                               irreps_out=irreps_mid)
        
        self.tp2 = FullyConnectedTensorProduct(irreps_in1=irreps_mid,
                                               irreps_in2=self.irreps_sh,
                                               irreps_out=irreps_out)
        
        self.irreps_out = self.tp2.irreps_out

    def forward(self, data):
        num_neighbors = 11
        num_nodes = 12
        
        # tensors of indices representing the graph
        edge_src, edge_dst = radius_graph(x=data.pos, r=self.r, batch=data.batch)
        edge_vec = data.pos[edge_src] - data.pos[edge_dst]
        edge_sh = o3.spherical_harmonics(l=self.irreps_sh, x=edge_vec, normalize=False, normalization='component')
    
        # For each node, the initial features are the sum of the spherical harmonics of the neighbors
        node_features = scatter(edge_sh, edge_dst, dim=0).div(num_neighbors**0.5)

        # For each edge, tensor product the features on the source node with the spherical harmonics
        edge_features = self.tp1(node_features[edge_src], edge_sh)
        node_features = scatter(edge_features, edge_dst, dim=0).div(num_neighbors**0.5)

        edge_features = self.tp2(node_features[edge_src], edge_sh)
        # node_features = scatter(edge_features, edge_dst, dim=0).div(num_neighbors**0.5)
        node_features = scatter(edge_features, edge_dst, dim=0, reduce='mean')
        
        return node_features
    

model_kwargs = {
    "irreps_in": None, 
    "irreps_hidden": e3nn.o3.Irreps('8x0e + 8x0o + 16x1e + 16x1o + 8x2e + 8x2o'),  # hyperparameter
    "irreps_out": "1x1o",  # 12 vectors out, but only 1 vector out per input
    "irreps_node_attr": None,
    "irreps_edge_attr": e3nn.o3.Irreps.spherical_harmonics(3),
    "layers": 3, 
    "max_radius": 3.5,
    "number_of_basis": 10,
    "radial_layers": 1,
    "radial_neurons": 128,
    "num_neighbors": 11,  
    "num_nodes": 12, 
    "reduce_output": False,  # setting this to true would give us one scalar as an output.
}

After defining these models, let go ahead to reuse the training codes.

# test training 

epochs = 1000
lr = 1e-3
e3nn_small, e3nn_small_logs = train(EquivariantPolynomial(), dataloaders['dx']['no_shuffle']['train'], dataloaders['dx']['no_shuffle']['test'], epochs=epochs, lr=lr)
e3nn_large, e3nn_large_logs = train(Network(**model_kwargs), dataloaders['dx']['no_shuffle']['train'], dataloaders['dx']['no_shuffle']['test'], epochs=epochs, lr=lr)

e3nn_small_y_hat, y = forward_pass(e3nn_small, dx_prediction_test_dataset, delta=True)
show_correlation(e3nn_small_y_hat, y)
compare_trajectories(e3nn_small_y_hat, y)

e3nn_large_y_hat, y2 = forward_pass(e3nn_large, dx_prediction_test_dataset, delta=True)
assert torch.allclose(y, y2)
show_correlation(e3nn_large_y_hat, y)
compare_trajectories(e3nn_large_y_hat, y)

epoch  1000 | Train MSE 10.74854   | Test MSE 0.36630   : 100%|██████████| 1001/1001 [10:59<00:00,  1.52it/s]
epoch  1000 | Train MSE 0.00000    | Test MSE 0.00006   : 100%|██████████| 1001/1001 [51:30<00:00,  3.09s/it]
100%|██████████| 410/410 [00:02<00:00, 147.40it/s]
100%|██████████| 410/410 [00:06<00:00, 60.48it/s]

The training speed is significantly slower due to the expensive FullyConnectedTensorProduct layer as it operates on higher order irreps.

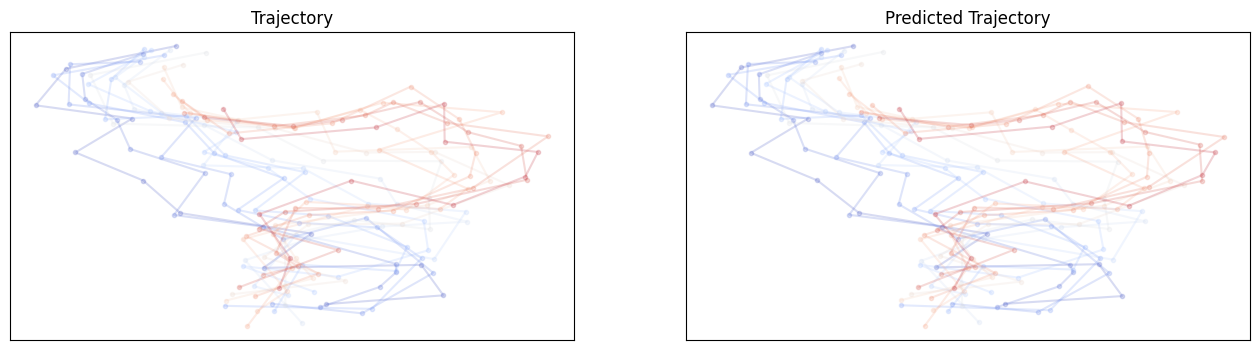
For E3NN small no shuffle:

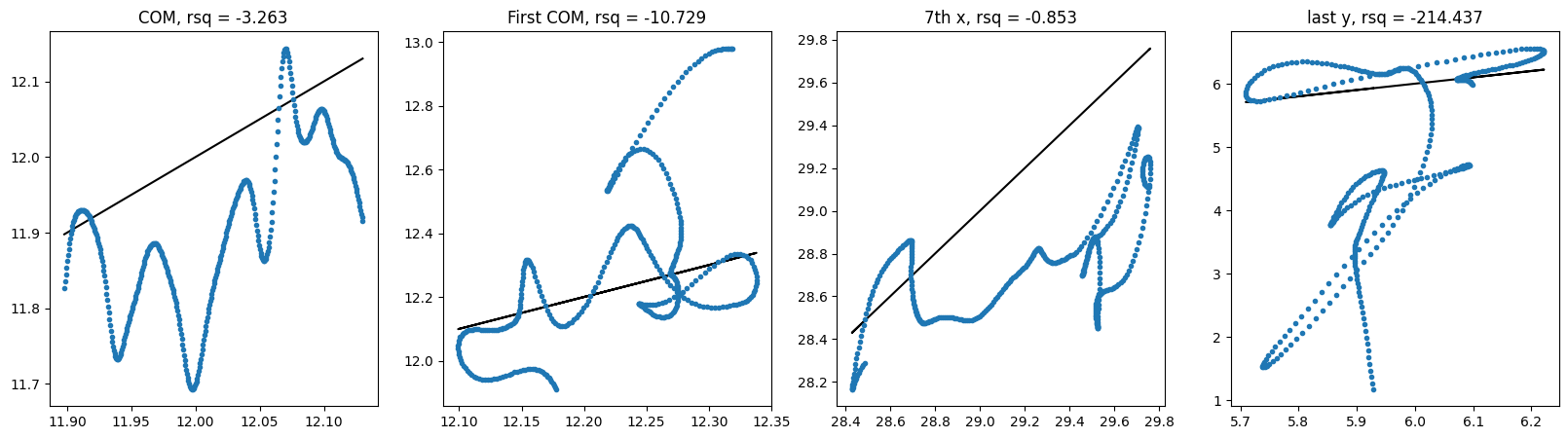
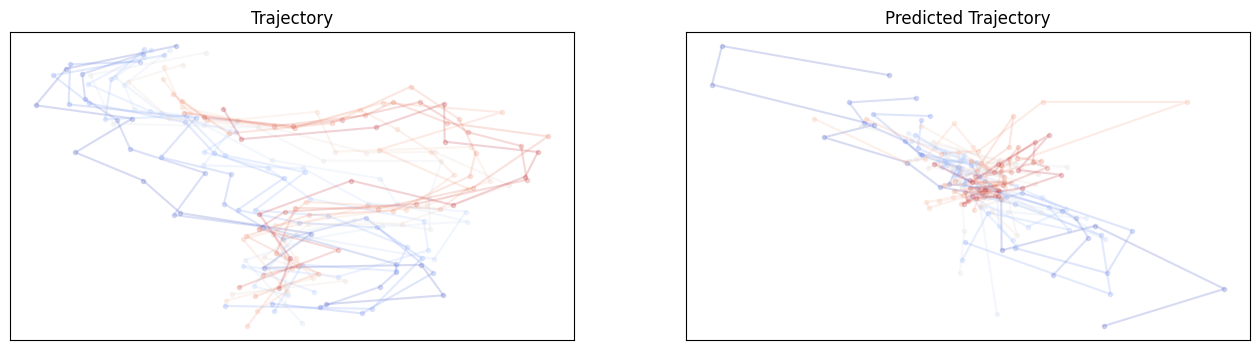
For E3NN large no shuffle:

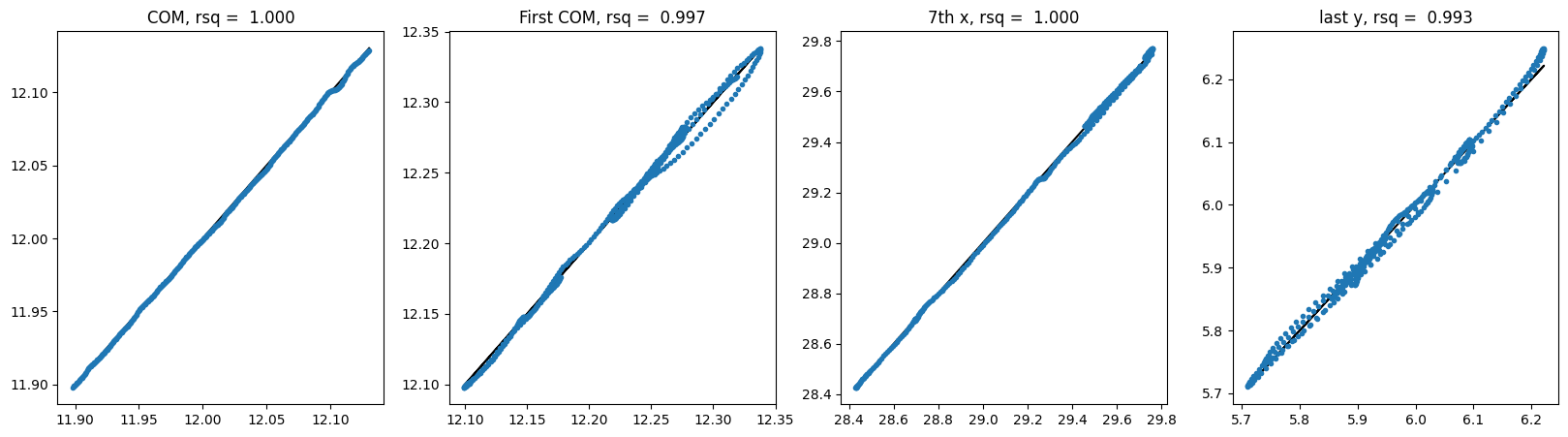
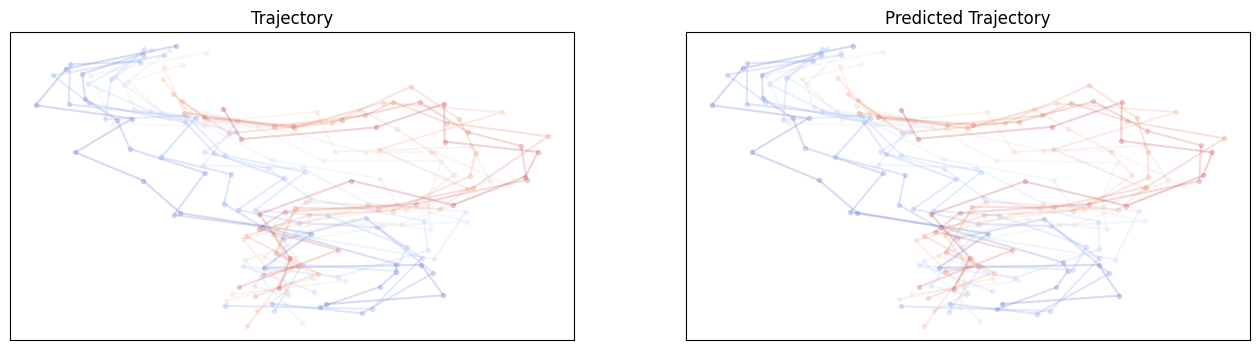
Hmmm.. It does not seem like these equivariant models outperform non-equivariant ones but the larger model involving higher order irreps definitely helps. It is unclear whether these models require different learning rates or longer training epochs.

I also tried to train them using the shuffled data sets but the results look similar without significant improvement.

In our set-up, we have the option to predict \(x(t+\Delta t)\) directly. Let’s see if we can directly train the e3nn_large using the positions directly.

epochs = 1000
lr = 1e-3
# e3nn_small, e3nn_small_logs = train(EquivariantPolynomial(), dataloaders['dx']['no_shuffle']['train'], dataloaders['dx']['no_shuffle']['test'], epochs=epochs, lr=lr, device='cpu', opt='AdamW')
e3nn_large2, _ = train(Network(**model_kwargs), dataloaders['pos']['no_shuffle']['train'], dataloaders['pos']['no_shuffle']['test'], epochs=epochs, lr=lr)

# e3nn_small_y_hat, y = forward_pass(e3nn_small, dx_prediction_test_dataset, delta=True)
# show_correlation(e3nn_small_y_hat, y)
# compare_trajectories(e3nn_small_y_hat, y)

e3nn_large_y_hat, y2 = forward_pass(e3nn_large2, pos_prediction_test_dataset, delta=False)
# assert torch.allclose(y, y2)
show_correlation(e3nn_large_y_hat, y2)
compare_trajectories(e3nn_large_y_hat, y2)

epoch  1000 | Train MSE 3.05509    | Test MSE 698.58898 : 100%|██████████| 1001/1001 [53:10<00:00,  3.19s/it]
100%|██████████| 410/410 [00:06<00:00, 62.76it/s]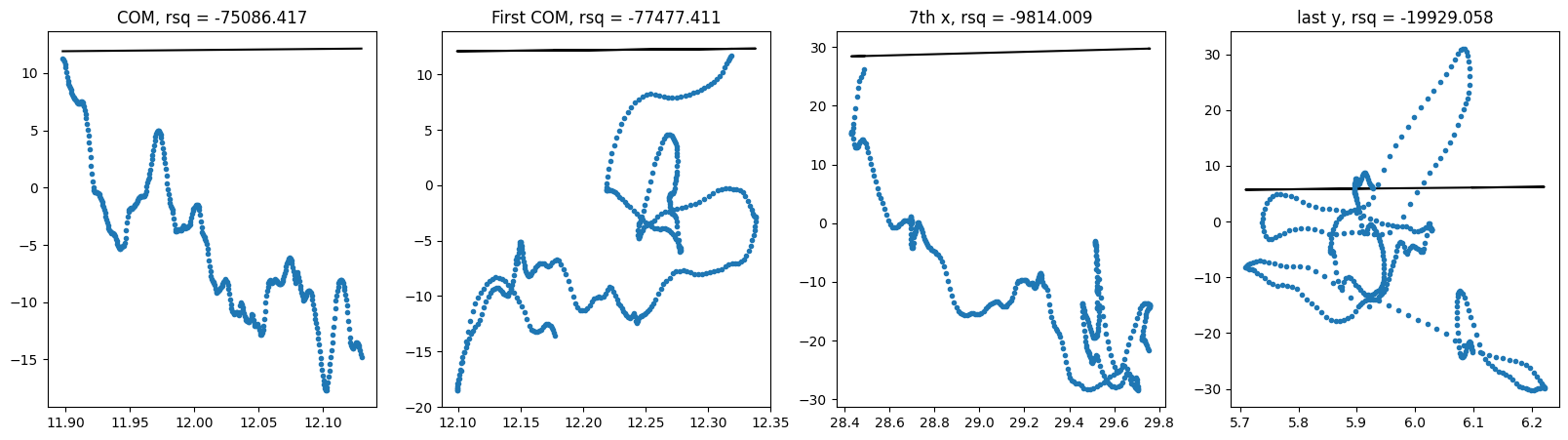

It does not seem to work. This might suggest that \(p(x(t + \Delta t) \| x(t))\) is different from \(p(\Delta x \| x(t))\) and is more diffucult to learn from the data in this setup.

2.5 Testing Equivariance

We will test equivariance of our 4 models so far.

# test se3 equivariance 
def se3_equivariance(model, rot=None, t=None, tol=1e-4):

    if rot is None: rot = trans.Rotation.from_euler('x', 37, degrees=True)
    if t is None: t = torch.zeros(1, 3)

    input_point = torch.randn(12, 3)
    input_point_transformed = torch.from_numpy(rot.apply(input_point)).to(torch.float) + t

    dset = [Data(pos=input_point, y=input_point)]
    dset_transformed = [Data(pos=input_point_transformed, y=input_point_transformed)]

    output_point, __ = forward_pass(model, dset)
    output_point_transformed = torch.from_numpy(rot.apply(output_point.squeeze(0))).to(torch.float)
    trandformed_output_point, __ = forward_pass(model, dset_transformed)

    err = (trandformed_output_point - output_point_transformed).abs().max().item()
    print('Err = ', err)
    # assert err < tol

    return None

print('MLP Baseline: ')
se3_equivariance(mlpbase)

print('GNN Baseline: ')
se3_equivariance(gnnbase)

print('E3NN Small: ')
se3_equivariance(e3nn_small)


print('E3NN Large: ')
se3_equivariance(e3nn_large)

MLP Baseline: 
100%|██████████| 1/1 [00:00<00:00, 1642.25it/s]
100%|██████████| 1/1 [00:00<00:00, 2750.36it/s]
Err =  0.004440372344106436
GNN Baseline: 
100%|██████████| 1/1 [00:00<00:00, 211.60it/s]
100%|██████████| 1/1 [00:00<00:00, 365.26it/s]
Err =  0.013194178231060505
E3NN Small: 
100%|██████████| 1/1 [00:00<00:00, 23.25it/s]
100%|██████████| 1/1 [00:00<00:00, 204.99it/s]
Err =  0.0001068115234375
E3NN Large: 
100%|██████████| 1/1 [00:00<00:00, 61.12it/s]
100%|██████████| 1/1 [00:00<00:00, 63.11it/s]
Err =  2.8870999813079834e-08

2.6 Simple SE3-Transformer

Given that the e3nn_large model does not outperform the baselines, I was motivated to look into more complex models, such as the SE3-Transformer. The e3nn document provides simple implementation of SE3-Transformer using the e3nn framework. I will use the implementation for E3Attention which grounds the E3MultiHeadAttention. We will use the layers to build a more complex E3Network.

# Build a SE-3 Transformer model
import e3nn

class E3Attention(torch.nn.Module): 

    def __init__(self, irreps_in, irreps_q, irreps_k, irreps_out, num_bases, max_radius, sh_order=4,): 
        super(E3Attention, self).__init__()

        self.irreps_in = irreps_in
        self.irreps_q = irreps_q
        self.irresp_k = irreps_k
        self.irreps_out = irreps_out
        self.irreps_sh = o3.Irreps.spherical_harmonics(sh_order)

        self.num_bases = num_bases
        self.max_radius = max_radius

        # input to query
        self.to_q = o3.Linear(irreps_in, irreps_q).to(DEVICE)
        
        # input to key
        self.tp_k = o3.FullyConnectedTensorProduct(irreps_in, self.irreps_sh, irreps_k, shared_weights=False).to(DEVICE)
        self.fc_k = e3nn.nn.FullyConnectedNet([self.num_bases, (sh_order + 1) ** 2, self.tp_k.weight_numel], act=torch.nn.functional.gelu).to(DEVICE)

        # input to value
        self.tp_v = o3.FullyConnectedTensorProduct(irreps_in, self.irreps_sh, irreps_out, shared_weights=False).to(DEVICE)
        self.fc_v = e3nn.nn.FullyConnectedNet([self.num_bases, (sh_order + 1) ** 2, self.tp_v.weight_numel], act=torch.nn.functional.gelu).to(DEVICE)

        # dot product
        self.dot_product = o3.FullyConnectedTensorProduct(irreps_q, irreps_k, '0e').to(DEVICE)


    def forward(self, data): 
        num_neighbors = 11
        num_nodes = 12
        
        pos = data.pos
        # features = torch.zeros(pos.shape[0], self.irreps_in.dim)
        features = pos
        

        # edges
        edge_src, edge_dst = radius_graph(pos, self.max_radius)
        edge_vec = pos[edge_src] - pos[edge_dst]
        edge_length = edge_vec.norm(dim=1)

        edge_length_embedded = e3nn.math.soft_one_hot_linspace(edge_length, start=0.0, end=self.max_radius, number=self.num_bases, basis='smooth_finite', cutoff=True) * self.num_bases ** 0.5
        edge_weight_cutoff = e3nn.math.soft_unit_step(10 * (1 - edge_length / self.max_radius))

        edge_features = o3.spherical_harmonics(self.irreps_sh, edge_vec, True, normalization='component').to(DEVICE)
        edge_length_embedded = edge_length_embedded.to(DEVICE)

        # qkv
        q = self.to_q(features)
        k = self.tp_k(features[edge_src], edge_features, self.fc_k(edge_length_embedded))
        v = self.tp_v(features[edge_src], edge_features, self.fc_v(edge_length_embedded))

        exp = edge_weight_cutoff[:, None] * self.dot_product(q[edge_dst], k).exp()
        exp = exp.clamp(0.0, 1.0)

        z = scatter(exp, edge_dst, dim=0, dim_size=len(features))
        z[z == 0] = 1
        alpha = exp / z[edge_dst]

        out = scatter(alpha.relu().sqrt() * v, edge_dst, dim=0, dim_size=len(features), reduce='mean')

        return out



class E3MultiHeadAttention(torch.nn.Module): 

    def __init__(self, irreps_in, irreps_q, irreps_k, irreps_mid, irreps_out, num_bases, max_radius, sh_order=4, heads=4): 
        super(E3MultiHeadAttention, self).__init__()
        self.irreps_in = irreps_in
        self.irreps_q = irreps_q
        self.irreps_k = irreps_k
        self.irreps_mid = irreps_mid
        self.irreps_out = irreps_out
        self.num_bases = num_bases
        self.max_radius = max_radius
        self.sh_order = sh_order
        self.heads = heads 

        self.irreps_all_heads = irreps_mid * heads
        self.irreps_sh = o3.Irreps.spherical_harmonics(sh_order)


        self.hs = [E3Attention(irreps_in, irreps_q, irreps_k, irreps_mid, num_bases=num_bases, max_radius=max_radius) for _ in range(heads)]
        
        self.tp1 = o3.FullyConnectedTensorProduct(self.irreps_all_heads, self.irreps_sh, self.irreps_mid)
        self.tp2 = o3.FullyConnectedTensorProduct(self.irreps_mid, self.irreps_sh, self.irreps_out)

    def forward(self, data): 

        pos = data.pos
        # features = torch.zeros(pos.shape[0], self.irreps_in.dim)
        features = pos
        
        # edges
        edge_src, edge_dst = radius_graph(pos, self.max_radius)
        edge_vec = pos[edge_src] - pos[edge_dst]
        edge_features = o3.spherical_harmonics(self.irreps_sh, edge_vec, True, normalization='component')

        hs = torch.concat([f(data) for f in self.hs], dim=1)
        # print(hs)

        h = self.tp1(hs[edge_src], edge_features)
        h = scatter(h, edge_dst, dim=0, reduce='mean')
        # print(h.shape)
        h = self.tp2(h[edge_src], edge_features)
        h = scatter(h, edge_dst, dim=0, reduce='mean')
        # print(h.shape)
        return h



class E3Network(torch.nn.Module): 
    
    def __init__(self, irreps_in, irreps_q, irreps_k, irreps_mid, irreps_out, num_bases, max_radius, sh_order=4, heads=4, layers=4): 
        super(E3Network, self).__init__()
        e3mhas = []
        for i in range(layers): 
            e3mhas.append(E3MultiHeadAttention(irreps_in=irreps_in, # if i == 0 else irreps_mid, 
                                               irreps_q=irreps_q, irreps_k=irreps_k, irreps_mid=irreps_mid,
                                               irreps_out=irreps_out, 
                                               num_bases=num_bases, max_radius=max_radius, sh_order=sh_order, 
                                               heads=heads))
        self.e3mhas = torch.nn.ModuleList(e3mhas)

    def forward(self, data): 
        tmp_data = data.clone()
        for (i, e3mha) in enumerate(self.e3mhas): tmp_data.pos = e3mha(tmp_data)
        return tmp_data.pos

Let’s get them trained. Note that GPU is required for training 1000 epochs here.

irreps_in = o3.Irreps("1x1o")
irreps_q = e3nn.o3.Irreps('8x0e + 8x0o + 16x1e + 16x1o + 8x2e + 8x2o')
irreps_k = irreps_q
irreps_mid = irreps_q
irreps_out = o3.Irreps("1x1o")

num_bases = 20
max_radius = 3.5


epochs = 300
lr = 1e-3
e3mha = E3MultiHeadAttention(irreps_in, irreps_q, irreps_k, irreps_mid, irreps_out, num_bases=num_bases, max_radius=max_radius, heads=16)
e3mha, _ = train(e3mha, dataloaders['dx']['no_shuffle']['train'], dataloaders['dx']['no_shuffle']['test'], epochs=epochs, lr=lr)

e3net = E3Network(irreps_in, irreps_q, irreps_k, irreps_mid, irreps_out, num_bases=num_bases, max_radius=max_radius, heads=8, layers=4)
e3net, _ = train(e3net, dataloaders['dx']['no_shuffle']['train'], dataloaders['dx']['no_shuffle']['test'], epochs=epochs, lr=lr)


e3mha_y_hat, y = forward_pass(e3mha, dx_prediction_test_dataset, delta=True)
show_correlation(e3mha_y_hat, y)
compare_trajectories(e3mha_y_hat, y)

e3net_y_hat, y = forward_pass(e3net, dx_prediction_test_dataset, delta=True)
show_correlation(e3net_y_hat, y)
compare_trajectories(e3net_y_hat, y)

  0%|          | 0/1 [01:45<?, ?it/s]
epoch   300 | Train MSE 0.00029    | Test MSE 0.00112   : 100%|██████████| 301/301 [1:58:21<00:00, 23.59s/it]
epoch    57 | Train MSE 0.00002    | Test MSE 0.00002   :  19%|█▉        | 58/301 [56:27<3:56:26, 58.38s/it]

(Note that the training was clipped due to disconnection from jupyter lab.)

Let’s see how the trained models perform.

e3mha_y_hat, y = forward_pass(e3mha, dx_prediction_test_dataset, delta=True)
show_correlation(e3mha_y_hat, y)
compare_trajectories(e3mha_y_hat, y)

e3net_y_hat, y = forward_pass(e3net, dx_prediction_test_dataset, delta=True)
show_correlation(e3net_y_hat, y)
compare_trajectories(e3net_y_hat, y)

For SE3 MHA no shuffle:

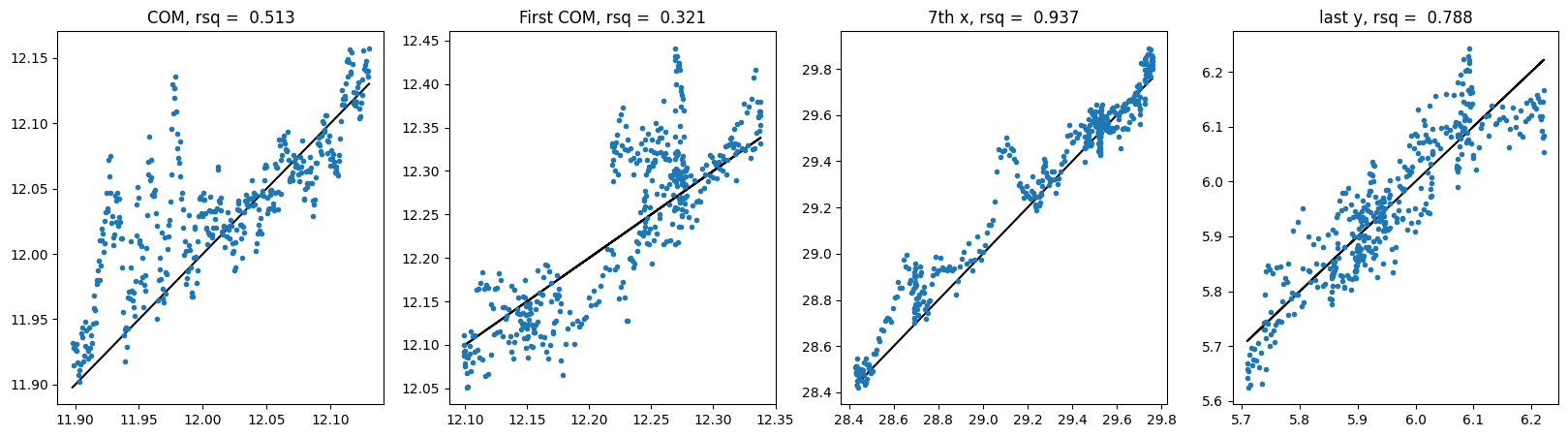
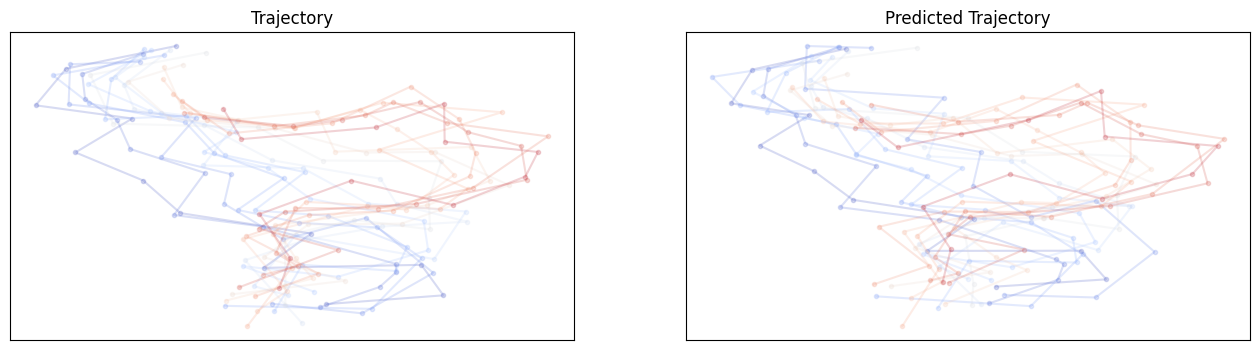
For SE3 Transformer no shuffle:

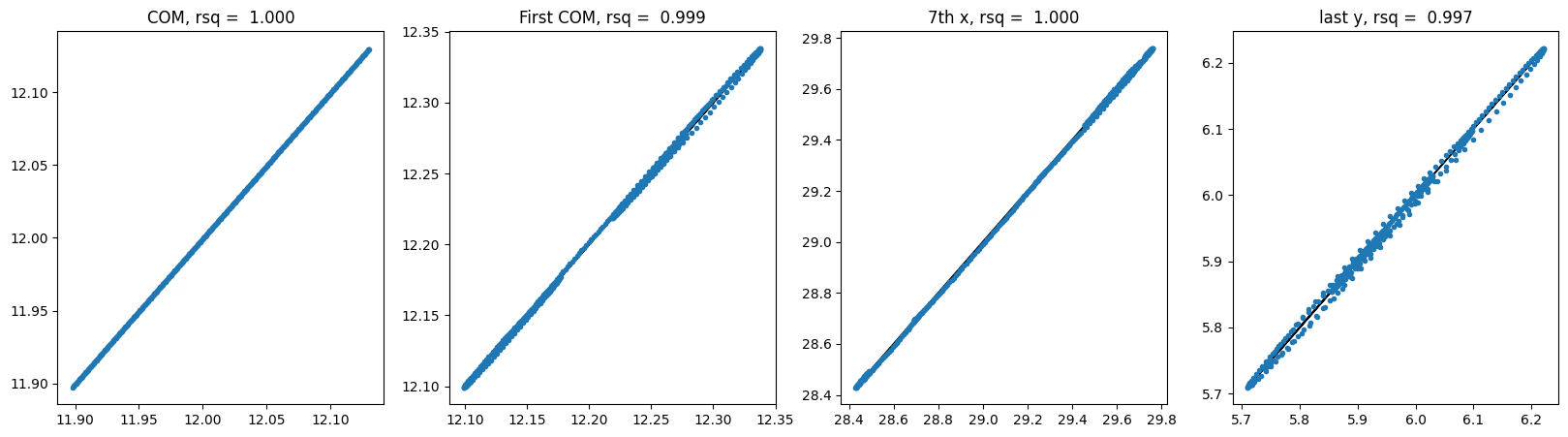
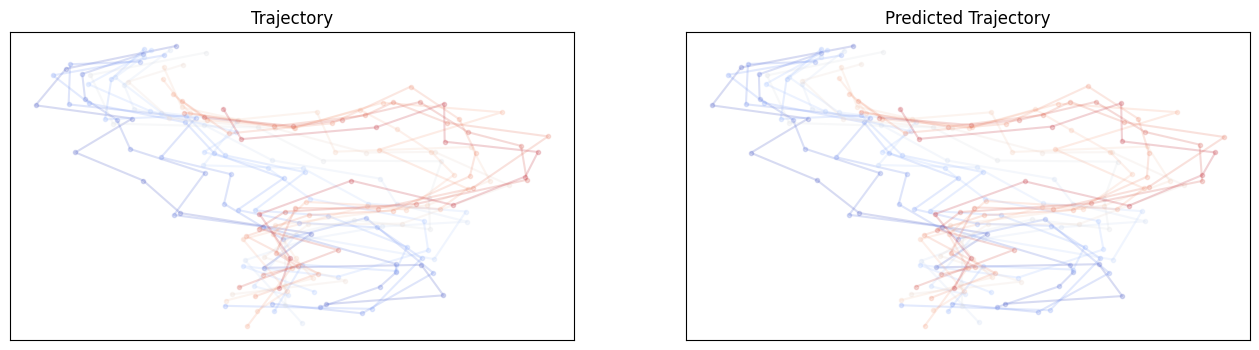
Let’s test the equivariance again

e3att = E3Attention(irreps_in, irreps_q, irreps_k, irreps_out, num_bases, max_radius)
print('E3ATT: ')
se3_equivariance(e3att)
# print(sum(p.numel() for p in e3att.parameters() if p.requires_grad))

e3mha = E3MultiHeadAttention(irreps_in, irreps_q, irreps_k, irreps_mid, irreps_out, num_bases=num_bases, max_radius=max_radius)
print('E3MHA: ')
se3_equivariance(e3mha)
# print(sum(p.numel() for p in e3mha.parameters() if p.requires_grad))


e3net = E3Network(irreps_in, irreps_q, irreps_k, irreps_mid, irreps_out, num_bases=num_bases, max_radius=max_radius, layers=4)
print('E3Net: ')
se3_equivariance(e3net)
# print(sum(p.numel() for p in e3net.parameters() if p.requires_grad))

E3ATT: 
3.576e-7

E3MHA: 
2.129e-7

E3NET:
1.781e-8

2.7 Summary

Here is the summary table of the experiments using the trajectory data.

model	trained on	shuffle	cm corr	p1 cm corr	p7 x corr	p12 y corr	equivariance err
MLPBase	dx	no	1.000	0.999	1.000	0.997	4.44e-3
MLPBase_SH	dx	yes	1.000	0.998	1.000	0.997
GNNBase	dx	no	1.000	0.999	1.000	0.996	1.32e-2
GNNBase_SH	dx	yes	1.000	0.999	0.999	0.997
E3Small	dx	no	-3.263	-10.729	-0.853	-214.437	1.07e-4
E3Small_SH	dx	yes	0.998	0.830	0.992	0.772
E3Large	dx	no	1.000	0.997	1.000	0.993	2.89e-8
E3Large_SH	dx	yes	0.999	0.993	0.999	0.990
E3Large_Pos	x	no	-75086	-77477	-9814	-19929
SE3MHA	dx	no	0.513	0.321	0.937	0.788	2.13e-7
SE3Trans	dx	no	1.000	0.999	1.000	0.997	1.78e-8

2.8 Notes

In the models that utilize FullyConnectedTensorProduct from e3nn, it might be interesting to see the weights between different order of features. Intuitively, the coefficients of higher order interactions should be small compared to l0 and l1 features. However, I have not investigated it.

The model was using radius_graph with a given radius range for constructing the message passing graphs. Whether this is good enough and how one should choose the radius are potential factors for model improvements.

References

Deep learning for molecules and materials: https://dmol.pub/index.html
https://e3nn.org
https://docs.e3nn.org/en/latest/guide/transformer.html
SE3-Transformer: https://arxiv.org/abs/2006.10503