Recently, I have been working with equivariant or invariant models. The models leverage inductive bias in the data. For example, convolutional layers is translational equivariant. The messaging aggregation function in the graph neural networks is permutational invariant. Physical data is typically in 3D and the models should respect euclidean symmetries, E(3). If the model does not respect E(3) symmetry, it is usually required to augment the data by random rotation and translation, which is an infinite amount of augmented data and the model might be hard to optimize.

If \(f: V \to V\) is an equivariant function on \(G\) and \(g\) is a group operation in \(G\). We have a data \(x\) on some vector space \(V\). We have

\[f(g \circ x) = g \circ f(x)\]

I am going to explore a general framework e3nn, which has taken care of the equivariant operations using irreproducible representations, irreps. There are 3 cases/tasks I want to explore in this post:

Tetris shape prediction: Given 3D coordinates of the voxels of a tetris block, predict the shape. The coordinates might be randomly rotated or translated and the model needs to generalize.
Trajectory prediction: Given a 12-body system and coordinates at certain time, predict 12 coordinates at the next time step. The system and physical motions should be independent of the reference frame, therefore, if we rotate or translate the coordinates, the motions should be equivariant.
Electron density prediction: The electron density is usually represented by the linear combinations of spherical harmonics, \(Y^l_m\). The goal is to predict the coefficients, which fits nicely to the irreps in e3nn.

1. Tetris

Given 3D coordinates of the voxels of a tetris block, predict the shape. The coordinates might be randomly rotated or translated and the model needs to generalize.

1.1 Packages

We will use some basic packages like torch, geometric libraries torch_geometric and augmented torch libraries torch_cluster and torch_scatter. The main one I am going to use is the e3nn package.

# minimal example for mesing with e3nn
import torch, logging
import numpy as np
import matplotlib.pyplot as plt

from torch_cluster import radius_graph
from torch_geometric.data import Data
from torch_geometric.loader import DataLoader
from torch_geometric.nn import GATConv
from torch_scatter import scatter

from e3nn import o3
from e3nn.o3 import FullyConnectedTensorProduct
from e3nn.util.test import assert_equivariant
from e3nn.nn.models.gate_points_2101 import Network

from tqdm.auto import tqdm

1.2 Tetris toy dataset

Each tetris block contain 4 voxels of size 1x1x1. There are 8 different shapes.

def tetris(shuffle=True):
    pos = [
        [(0, 0, 0), (0, 0, 1), (1, 0, 0), (1, 1, 0)],  # chiral_shape_1
        [(0, 0, 0), (0, 0, 1), (1, 0, 0), (1, -1, 0)],  # chiral_shape_2
        [(0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 1, 0)],  # square
        [(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 0, 3)],  # line
        [(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0)],  # corner
        [(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 1, 0)],  # L
        [(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 1, 1)],  # T
        [(0, 0, 0), (1, 0, 0), (1, 1, 0), (2, 1, 0)],  # zigzag
    ]
    pos = torch.tensor(pos, dtype=torch.get_default_dtype())

    # Since chiral shapes are the mirror of one another we need an *odd* scalar to distinguish them
    labels = torch.tensor(
        [
            [+1, 0, 0, 0, 0, 0, 0],  # chiral_shape_1
            [-1, 0, 0, 0, 0, 0, 0],  # chiral_shape_2
            [0, 1, 0, 0, 0, 0, 0],  # square
            [0, 0, 1, 0, 0, 0, 0],  # line
            [0, 0, 0, 1, 0, 0, 0],  # corner
            [0, 0, 0, 0, 1, 0, 0],  # L
            [0, 0, 0, 0, 0, 1, 0],  # T
            [0, 0, 0, 0, 0, 0, 1],  # zigzag
        ],
        dtype=torch.get_default_dtype(),
    )

    # apply shuffling of data
    if shuffle: 
        idx = torch.randperm(8)
        pos = pos[idx]
        labels = labels[idx]

    # apply random rotation
    pos = torch.einsum("zij,zaj->zai", o3.rand_matrix(len(pos)), pos)

    # put in torch_geometric format
    dataset = [Data(pos=pos) for pos in pos]
    data = next(iter(DataLoader(dataset, batch_size=len(dataset))))

    return data, labels

Note that the chiral shape has parity, i.e. the label of the chiral shape is a pseudo-scalar, which flip signs upon mirror reflection.

Everything should look familiar, maybe except for o3.rand_matrix(n). It generates \(n\) 3x3 random rotational matrices, which were applied to the coordinates.

Let’s take a look at the data.


1
2
3
 data, labels = tetris(shuffle=False)
print(data)
print(data.pos.shape)

Output:

DataBatch(pos=[32, 3], batch=[32], ptr=[9])
torch.Size([32, 3])

The data follows the torch_geometric convention where batch represents which graph the positions belong to and the ptr is the pointer to the start of each graph.

1.3 GNN Baseline

Let’s build a simple GNN baseline model using message passing with attention: GATConv.

# GNN base line
class GNN(torch.nn.Module): 
    
    def __init__(self, dim_in=16, edge_dim=16, hidden_dim=256, dim_out=7, heads=4): 
        super(GNN, self).__init__()
        self.dim_in = dim_in
        self.edge_dim = edge_dim
        self.hidden_dim = hidden_dim
        self.dim_out = dim_out
        self.heads = heads

        # irreps of spherical harmonics
        self.irreps_sh = o3.Irreps.spherical_harmonics(3)
        
        self.gat1 = GATConv(dim_in, hidden_dim, edge_dim=edge_dim, heads=heads)
        self.gat2 = GATConv(hidden_dim * heads, hidden_dim, edge_dim=edge_dim, heads=heads)
        self.head = torch.nn.Sequential(torch.nn.Linear(hidden_dim * heads, hidden_dim),
                                        torch.nn.GELU(),
                                        torch.nn.Linear(hidden_dim, dim_out))
        
    def forward(self, data):

        num_neighbors = 3
        num_nodes = 4
        
        # tensors of indices representing the graph, using fully connected
        edge_index = radius_graph(x=data.pos, r=10.1, batch=data.batch)
        edge_src, edge_dst = edge_index
        edge_vec = data.pos[edge_src] - data.pos[edge_dst]
        
        edge_features = o3.spherical_harmonics(l=self.irreps_sh, x=edge_vec, normalize=False, normalization='component')
        node_features = scatter(edge_features, edge_dst, dim=0).div(num_neighbors**0.5)

        # GNN message passing
        x = self.gat1(node_features, edge_index, edge_attr=edge_features)
        x = self.gat2(x, edge_index, edge_attr=edge_features)
        x = scatter(x, data.batch, dim=0).div(num_nodes**0.5)
        return self.head(x)

Again, this is a very typical GNN and forward pass. However, there are some foreign stuff sneaking in the code and I’ll explain. Since the input or the data only contains a set of 4 coordinates, (x, y, z). The node and edge contain absolutely no features at all except for the coordinates. I am going to use, again, spherical harmonics to featurize the edges and nodes.

The line self.irreps_sh = o3.Irreps.spherical_harmonics(3) is the basis of the spherical harmonics, containing the following irreps:

o3.Irreps.spherical_harmonics(3)

1x0e+1x1o+1x2e+1x3o

Ok and let me expand these weird codes. There are 4 irreps in the above expression. Each irrep is of the form of mxlp, where

m is the multiplicity, i.e. the number of features
x just stands for times
l is the rotation order, or the first quantum number of electron orbitals or the order of spherical harmonics.
- l = 0 is transformed as scalar (one number), or the l = 0 orbital, which is a sphere.
- l = 1 is transformed as vector (three numbers), or the l = 1 orbital, which aligns with the x, y, z axes, corresponding to 3 quantum numbers m = -1, 0, 1.
- l = 2 is transformed as ?…? (five numbers), or the l = 2 orbital, which are more complicated, corresponding to 5 quantum numbers m = -2, -1, 0, 1, 2.
p describes the parity: even e or odd o, describing how these tensors transform under mirror reflection.

So 16x1o is a set of 16 vectors with odd parity.

Another line is the radius_graph(x=data.pos, r=10.1, batch=data.batch) which constructs the edge_index just using the coordinates and batch. I used r = 10.1 or something r > 3.1 to construct the fully connected graph of 4 nodes. These edges are directional, because they are translational vectors. So in the above line, we will have 4 * 3 = 12 edges for each graph. Therefore,

radius_graph(x=data.pos, r=10.1, batch=data.batch).shape
# 12 * 8 (graphs) edges in total

torch.Size([2, 96])

Since the input is only the 3D coordinates, the straightforward featurization is using the distance vector, \(\mathbf{r}_i - \mathbf{r}_j\) where \(\mathbf{r}\) is the position vector. We further use the coefficients of spherical harmonics as edge features, i.e. we project the distance vector on l=0, 1, 2, 3 spherical harmonics and get the coefficients, with a total number of 1 + 3 + 5 + 7 = 16 coefficients. Note that \(<Y^l_m, Y^{l'}_{m'}> = \delta_{ll'}\delta_{mm'}\), meaning that they are orthogonal bases.

edge_features = o3.spherical_harmonics(l=self.irreps_sh, x=edge_vec, normalize=False, normalization='component')
# 96 (edges) x 16 (edge features) tensor

The node features are the aggregated of the edge features of the inward edges.

node_features = scatter(edge_features, edge_dst, dim=0).div(num_neighbors**0.5)
# 32 (nodes) x 16 (node features) tensor

With the node and edge features using spherical harmonics, we can just create a graph convolution and a readout for tetris shape prediction.

Let’s build a general training function that can be used for all the models built for this task.

# model training script 

def train(model, epochs=1000, lr=1e-4, shuffle=False):

    model.train()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    loss_fn = torch.nn.MSELoss()

    every_n = epochs // 100
    logs = dict({'loss': np.zeros(epochs + 1), 'accuracy': np.zeros(epochs + 1)})
    pbar = tqdm(range(epochs + 1))
    for step in pbar: 
        data, labels = tetris(shuffle=shuffle)
        pred = model(data)
        loss = loss_fn(pred, labels)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        acc = pred.round().eq(labels).all(dim=1).double().mean(dim=0).item()
        logs['loss'][step] = loss.item()
        logs['accuracy'][step] = acc

        s = f'epoch {step:5d} | loss {1e3 * loss:<10.1f} | {100 * acc:5.1f}% accuracy'
        if step % every_n == 0: pbar.set_description(s)
    
    return model, logs

Now we can try to train our GNN baseline model:

g, g_logs = train(GNN(), epochs=10000, lr=1e-4, shuffle=False)
g_shuffle, g_shuffle_logs = train(GNN(), epochs=10000, lr=1e-4, shuffle=True)

# epoch 10000 | loss 41.9       |  75.0% accuracy: 100%|██████████| 10001/10001 [01:25<00:00, 117.05it/s]
# epoch 10000 | loss 40.5       |  75.0% accuracy: 100%|██████████| 10001/10001 [01:25<00:00, 116.74it/s]

Training on CPU took about 90 seconds for 10000 epochs. We tried no shuffling and shuffling and the final loss were \(41.9\) and \(40.5\) respectively. They achieved final accuracy of \(75\%\), which is not optimal given the easiness of the task and small number of data and large GNN models with GATConv.

1.4 E3NN

In previous GNN model, I used a small part of e3nn for featurization but the model is still not aware of the E(3) symmetry: it just did something like torch.nn.Linear and ignored the relationship/interaction of each element under E(3). We were also toruched on the irreps, which I feel it might be better to go through them again.

# We have seen the irreps for spherical harmonics with lmax = 3
irreps_sh = o3.Irreps.spherical_harmonics(3)
# 1x0e + 1x1o + 1x2e + 1x3o representing spherical harmonics of lmax = 3

Similar to the hidden dimension in the hidden layers of neural networks, we can also define the hidden irreps in e3nn.

irreps_mid = o3.Irreps('64x0e + 24x1e + 24x1o + 16x2e + 16x2o')
# 64x0e = 64 hidden scalar, l = 0
# 24x1e = 24 hidden pseudo-vector, l = 1
# 24x1o = 24 hidden vector, l = 1
# 16x2e = 16 even tensor, l = 2
# 16x2o = 16 odd tensor, l=2
# So we have 64 + 24 x 3 + 24 x 3 + 16 x 5 + 16 x 5 = 368 dim tensor as output of the hidden layer.

The neural network layer (or the Linear layer) in e3nn is called the FullyConnectedTensorProduct with trainable weights. At initialization, it takes 2 input irreps and 1 output 1rreps and in the forward pass, it takes 2 tensors with corresponding input irreps. This layer dictates the interaction between different irreps.

# tensor product 1
tp1 = FullyConnectedTensorProduct(irreps_in1=irreps_sh, irreps_in2=irreps_sh, irreps_out=irreps_mid)
# each path corresponds to one parameters, the path is defined by |l1 - l2| <= lout <= l1 + l2
# the above layer contains 648 paths and therefore 648 parameters
# this can be shown: 64 * 4 (0e) + 24 * 3 (1e) + 24 * 6 (1o) + 16 * 7 (2e) + 16 * 4 (2o)

We can check if the above tensor product is the same as exhausting all possible paths of the irreps.

# or we can check this: 
npaths = 0
for in1 in ['1x0e', '1x1o', '1x2e', '1x3o']: 
    for in2 in ['1x0e', '1x1o', '1x2e', '1x3o']:
        for out in ['64x0e', '24x1e', '24x1o', '16x2e', '16x2o']: 
            p = FullyConnectedTensorProduct(irreps_in1=o3.Irreps(in1), 
                                                  irreps_in2=o3.Irreps(in2), 
                                                  irreps_out=o3.Irreps(out)).weight.shape[0]
            npaths += p
            if p > 0: print(f'{in1} + {in2} -> {out}, {p}')
assert npaths == tp1.weight.shape[0]

# The output: 
# 1x0e + 1x0e -> 64x0e, 64
# 1x0e + 1x1o -> 24x1o, 24
# 1x0e + 1x2e -> 16x2e, 16
# 1x1o + 1x0e -> 24x1o, 24
# 1x1o + 1x1o -> 64x0e, 64
# 1x1o + 1x1o -> 24x1e, 24
# 1x1o + 1x1o -> 16x2e, 16
# 1x1o + 1x2e -> 24x1o, 24
# 1x1o + 1x2e -> 16x2o, 16
# 1x1o + 1x3o -> 16x2e, 16
# 1x2e + 1x0e -> 16x2e, 16
# 1x2e + 1x1o -> 24x1o, 24
# 1x2e + 1x1o -> 16x2o, 16
# 1x2e + 1x2e -> 64x0e, 64
# 1x2e + 1x2e -> 24x1e, 24
# 1x2e + 1x2e -> 16x2e, 16
# 1x2e + 1x3o -> 24x1o, 24
# 1x2e + 1x3o -> 16x2o, 16
# 1x3o + 1x1o -> 16x2e, 16
# 1x3o + 1x2e -> 24x1o, 24
# 1x3o + 1x2e -> 16x2o, 16
# 1x3o + 1x3o -> 64x0e, 64
# 1x3o + 1x3o -> 24x1e, 24
# 1x3o + 1x3o -> 16x2e, 16

And we can visualize these interaction paths:

tp1.visualize()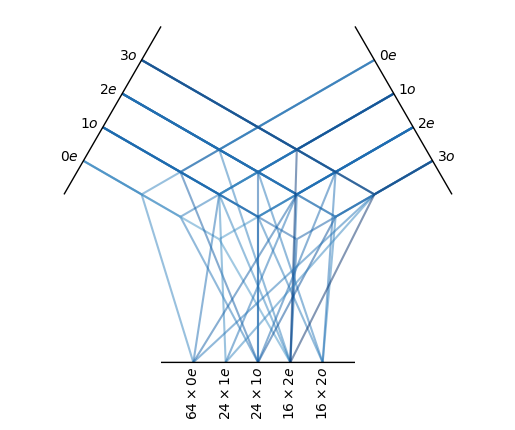

Now we can define our simple equivariant model using e3nn’s FullyConnectedTensorProduct.

class InvariantPolynomial(torch.nn.Module):

    def __init__(self):
        super(InvariantPolynomial, self).__init__()

        self.irreps_sh = o3.Irreps.spherical_harmonics(3) 
        # dimension = 16 = 1 + 3 + 5 + 7
        
        irreps_mid = o3.Irreps('64x0e + 24x1e + 24x1o + 16x2e + 16x2o') 
        # dimension = 368 = (64 * 1) + (24 * 3) + (24 * 3) + (16 * 5) + (16 * 5)
        
        irreps_out = o3.Irreps('0o + 6x0e') 
        # dimension = (1 * 1) + (6 * 1), the first one is the pseudo-scalar for chiral +1, -1

        self.tp1 = FullyConnectedTensorProduct(irreps_in1=self.irreps_sh, 
                                               irreps_in2=self.irreps_sh,
                                               irreps_out=irreps_mid)
        
        self.tp2 = FullyConnectedTensorProduct(irreps_in1=irreps_mid,
                                               irreps_in2=self.irreps_sh,
                                               irreps_out=irreps_out)
        
        self.irreps_out = self.tp2.irreps_out

    def forward(self, data):
        num_neighbors = 2
        num_nodes = 4
        
        # tensors of indices representing the graph
        edge_src, edge_dst = radius_graph(x=data.pos, r=1.1, batch=data.batch)
        
        # edge distance vector
        edge_vec = data.pos[edge_src] - data.pos[edge_dst]
        
        edge_sh = o3.spherical_harmonics(l=self.irreps_sh, x=edge_vec, normalize=False, normalization='component')
        # edge_sh is the coefficients of spherical harmonics from l=0 to l=3
        # or edge_sh is the projection of edge_vec on spherical harmonics basis
        # edge_sh is a 50 (number of edges by `radius_graph`) x 16 (l=3 spherical harmonics, i.e. 1 + 3 + 5 + 7) 
        
        
        # For each node, the initial features are the sum of the spherical harmonics of the neighbors
        node_features = scatter(edge_sh, edge_dst, dim=0).div(num_neighbors**0.5)


        # For each edge, tensor product the features on the source node with the spherical harmonics
        edge_features = self.tp1(node_features[edge_src], edge_sh)
        node_features = scatter(edge_features, edge_dst, dim=0).div(num_neighbors**0.5)
        

        edge_features = self.tp2(node_features[edge_src], edge_sh)
        node_features = scatter(edge_features, edge_dst, dim=0).div(num_neighbors**0.5)


        # For each graph, all the node's features are summed as final prediction
        return scatter(node_features, data.batch, dim=0).div(num_nodes**0.5)

We use the train function again.

f, f_logs = train(InvariantPolynomial(), epochs=10000, lr=1e-4, shuffle=False)
f_shuffle, f_shuffle_logs = train(InvariantPolynomial(), epochs=10000, lr=1e-4, shuffle=True)
# epoch 10000 | loss 7.3        | 100.0% accuracy: 100%|██████████| 10001/10001 [00:41<00:00, 241.84it/s]
# epoch 10000 | loss 2.0        | 100.0% accuracy: 100%|██████████| 10001/10001 [00:41<00:00, 243.12it/s]

Clearly, the model was trained better due to the E(3) equivariance. No shuffling and shuffling model achieved a final loss of \(7.3\) and \(2.0\) respectively with \(100\%\) accuracy, which is a lot better than the GNN baseline.

1.5 Fancy E3NN

I have seen some people use the existent model of e3nn instead of writing the FullyConnectedTensorProduct. We will use this fancier model from e3nn: gate_points_2101.Network.

We start off by assigning some hyperparameter:

model_kwargs = {
    "irreps_in": None,  # no input features
    "irreps_hidden": o3.Irreps('64x0e + 24x1e + 24x1o + 16x2e + 16x2o'),  # hyperparameter: hidden irreps
    "irreps_out": "0o + 6x0e",  # the same output irreps
    "irreps_node_attr": None,
    "irreps_edge_attr": o3.Irreps.spherical_harmonics(3), # using spherical(3) for featurization
    "layers": 3,  # hyperparameter: depth of the hidden irreps layer
    "max_radius": 1.1, 
    "number_of_basis": 10,
    "radial_layers": 1,
    "radial_neurons": 128,
    "num_neighbors": 2,  # average number of neighbors w/in max_radius
    "num_nodes": 4,  # not important unless reduce_output is True
    "reduce_output": False,  # setting this to true would give us one scalar as an output.
}

model = Network(**model_kwargs)

The output of the model is a 32 x 7 tensor, i.e. for each coordinate (regardless of the batch), the model outputs the 7-tensor. We need to aggregate these 4 7-tensors like before according to batch. So we created another wrapper model:

class InvariantNetwork(torch.nn.Module): 
    def __init__(self, model_kwargs=model_kwargs): 
        super(InvariantNetwork, self).__init__()
        self.model_kwargs = model_kwargs
        self.network = Network(**model_kwargs)
    
    def forward(self, data): 
        node_features = self.network(data)
        return scatter(node_features, data.batch, dim=0).div(self.model_kwargs['num_nodes']**0.5)

Again, we use our train function.

ff, ff_logs = train(InvariantNetwork(), epochs=10000, lr=1e-4, shuffle=False)
ff_shuffle, ff_shuffle_logs = train(InvariantNetwork(), epochs=10000, lr=1e-4, shuffle=True)
# epoch 10000 | loss 0.0        | 100.0% accuracy: 100%|██████████| 10001/10001 [04:12<00:00, 39.67it/s]
# epoch 10000 | loss 0.0        | 100.0% accuracy: 100%|██████████| 10001/10001 [04:17<00:00, 38.89it/s]

And.. take a look at those too-good-to-be-true losses and accuracies.

1.6 Comparisons

Let’s compare the 3 models trained: GNN, E3NN Basic, E3NN Fancy. We plot the training losses and accuracies using the logs.

fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].plot(g_logs['loss'], label='GNN', alpha=0.75)
axes[0].plot(g_shuffle_logs['loss'], label='GNN Shuffle', alpha=0.75)
axes[0].plot(f_logs['loss'], label='E3NNBasic', alpha=0.75)
axes[0].plot(f_shuffle_logs['loss'], label='E3NNBasic Shuffle', alpha=0.75)
axes[0].plot(ff_logs['loss'], label='E3NNFancy', alpha=0.75)
axes[0].plot(ff_shuffle_logs['loss'], label='E3NNFancy Shuffle', alpha=0.75)
axes[0].set_yscale('log')
axes[0].set_title('Loss')
axes[0].legend()

axes[1].plot(g_logs['accuracy'], label='GNN', alpha=0.75)
axes[1].plot(g_shuffle_logs['accuracy'], label='GNN Shuffle', alpha=0.75)
axes[1].plot(f_logs['accuracy'], label='E3NNBasic', alpha=0.75)
axes[1].plot(f_shuffle_logs['accuracy'], label='E3NNBasic Shuffle', alpha=0.75)
axes[1].plot(ff_logs['accuracy'], label='E3NNFancy', alpha=0.75)
axes[1].plot(ff_shuffle_logs['accuracy'], label='E3NNFancy Shuffle', alpha=0.75)
axes[1].set_title('Accuracy')
axes[1].legend()

plt.show()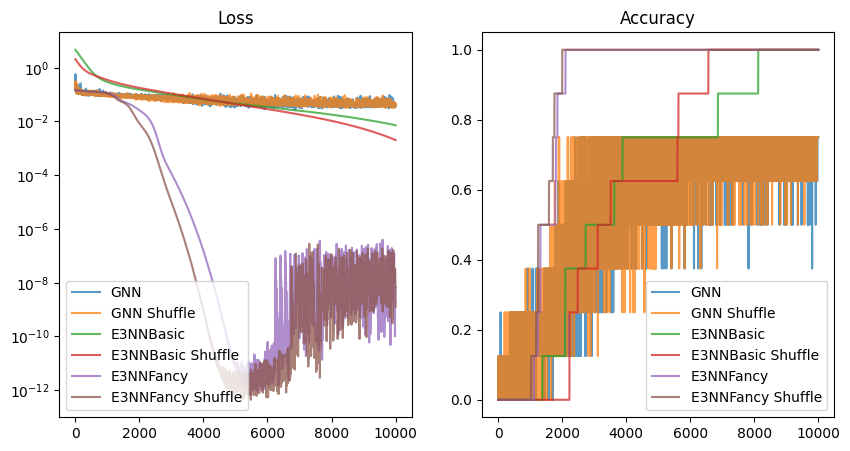

1.7 Check Equivariance

Finally, we need to check the model equivariance, using our very first equation

\[f(g \circ x) = g \circ f(x)\]

where \(g\) here is a 3D rotation or translation and \(f\) is our trained model. The model is acturally invariant, i.e. the output does not depend on the transformation of group operation.

\[f(g \circ x) = f(x)\]

# == Check equivariance ==
# Because the model outputs (psuedo)scalars, we can easily directly
# check its equivariance to the same data with new rotations:
print("Testing equivariance directly...")

data, _ = tetris(shuffle=False)
rotated_data, _ = tetris(shuffle=False)

# GNN
error = g(rotated_data) - g(data)
shuffle_error = g_shuffle(rotated_data) - g_shuffle(data)
print()
print(f"GNN: Equivariance error = {error.abs().max().item():.1e}")
print(f"GNN Shuffle: Equivariance error = {shuffle_error.abs().max().item():.1e}")

# E3NN Basic
error = f(rotated_data) - f(data)
shuffle_error = f_shuffle(rotated_data) - f_shuffle(data)
print()
print(f"E3NN Basic: Equivariance error = {error.abs().max().item():.1e}")
print(f"E3NN Basic Shuffle: Equivariance error = {shuffle_error.abs().max().item():.1e}")

# E3NN Fancy
error = ff(rotated_data) - ff(data)
shuffle_error = ff_shuffle(rotated_data) - ff_shuffle(data)
print()
print(f"E3NN Fancy: Equivariance error = {error.abs().max().item():.1e}")
print(f"E3NN Fancy Shuffle: Equivariance error = {shuffle_error.abs().max().item():.1e}")


# Testing equivariance directly...

# GNN: Equivariance error = 3.6e-01
# GNN Shuffle: Equivariance error = 3.3e-01

# E3NN Basic: Equivariance error = 9.5e-07
# E3NN Basic Shuffle: Equivariance error = 9.5e-07

# E3NN Fancy: Equivariance error = 5.5e-06
# E3NN Fancy Shuffle: Equivariance error = 5.7e-06

And we can test the equivariance using e3nn’s assert_equivariant function.

print("Testing equivariance using `assert_equivariance`...")
# We can also use the library's `assert_equivariant` helper
# `assert_equivariant` also tests parity and translation, and
# can handle non-(psuedo)scalar outputs.
# To "interpret" between it and torch_geometric, we use a small wrapper:

def fwrapper(pos, batch): return f(Data(pos=pos, batch=batch))
def ffwrapper(pos, batch): return ff(Data(pos=pos, batch=batch))

# `assert_equivariant` uses logging to print a summary of the equivariance error,
# so we enable logging
logging.basicConfig(level=logging.INFO)

assert_equivariant(
    fwrapper,
    args_in=[data.pos, data.batch], # We provide the original data that `assert_equivariant` will transform...
    irreps_in=[ # ...in accordance with these irreps...
        "cartesian_points",  # pos has vector 1o irreps, but is also translation equivariant
        None,  # `None` indicates invariant, possibly non-floating-point data
    ],
    irreps_out=[f.irreps_out], # ...and confirm that the outputs transform correspondingly for these irreps:
)

_ = assert_equivariant(ffwrapper, args_in=[data.pos, data.batch], irreps_in=["cartesian_points", None], irreps_out=[f.irreps_out])


# INFO:e3nn.util.test:Tested equivariance of `fwrapper` -- max componentwise errors:
# (parity_k=0, did_translate=False) -> max error=7.153e-07 in argument 0
# (parity_k=0, did_translate=True) -> max error=2.339e-06 in argument 0
# (parity_k=1, did_translate=False) -> max error=8.848e-07 in argument 0
# (parity_k=1, did_translate=True) -> max error=1.810e-06 in argument 0
# INFO:e3nn.util.test:Tested equivariance of `ffwrapper` -- max componentwise errors:
# (parity_k=0, did_translate=False) -> max error=2.742e-06 in argument 0
# (parity_k=0, did_translate=True) -> max error=1.824e-05 in argument 0
# (parity_k=1, did_translate=False) -> max error=3.345e-06 in argument 0
# (parity_k=1, did_translate=True) -> max error=2.146e-05 in argument 0
# Testing equivariance using `assert_equivariance`...

And this concludes the part 1 of initial messing around of e3nn.

References

Mario Geiger, Tess Smidt, e3nn: Euclidean Neural Networks, https://arxiv.org/abs/2207.09453
https://e3nn.org
https://docs.e3nn.org/en/latest/examples/tetris_polynomial.html