C4 Group CNN | Yen-Lin Chen

This was my learning process for the simple group convolution from scratch, which I did back in 2021 along with the Geometric Deep Learning (GDL) course. This is part of the tutorial 2, which can be found here. I was trying to remind myself of some of the key concepts by cleaning my previous codes and summarizing here for myself.

The key of the group equivariant neural network is to identify the spaces of input, hidden and output because the network will perform like a function mapping from one space to another. I use $X$, $Y$ as input and output spaces and $H_i$ as the i-th hidden space. The network consists a number of layers, transforming the input to hidden to output:

\[X \to H_1 \to H_2 \to ... \to H_i \to ... \to Y\]

Each of the layers is represented as $\to$ in the above and depneding on which spaces the layers map from and to, we need to consider the design of the layers. This will be the focus of this post.

0. Dependencies

Let’s just load some dependencies for later use.

# packages
import os, torch, einops

import numpy as np
import matplotlib.pyplot as plt

from PIL import Image
from tqdm.auto import tqdm
from torch.utils.data import Dataset
from torchvision.transforms import ToTensor

TOL = 1e-5
# if torch.cuda.is_available(): DEVICE = 'cuda'
# else: DEVICE = 'mps' if torch.backends.mps.is_available() else 'cpu'
DEVICE = 'cpu' # I find the 'mps' device is buggy or I have not spent time to write better code for the mac gpu

print(DEVICE)

1. Group

A group $(G, \circ )$ is a set $G$ with a binary operation: $\circ : G\times G \to G$, which satisfies the following (Ignored the $\circ$).

Associativity: $a (bc) = (ab) c$
Identity: $e \in G$, $g e = e g = g$
Inverse: $\forall g \in G$, $gg^{-1} = g^{-1}g = e$

Consider the group $G = C_4$, the cyclic group with $\pi / 2$ planar rotation. $\|C_4\| = 4$. Let $X$ be the set of some $n\times n$ gray images. An image $x \in X$ is a function $x: p \to x[p] \in R$ which maps each pixel $p = (h, w)$ to a real number.

An element $g \in G = C_4$, transforms an image $x \in X$ into the image $gx \in X$ through rotation. The rotated image $gx$ is $[gx](p) = x(g^{-1}p)$ where $g^{-1}p$ is the pixel in the unrotated image. This action is the following:

# rotate an image, the x is ... x H x W in dimension
def rotate(x, r): return x.rot90(r, dims=(-2, -1))

2. Equivariant Convolution Layers

An equivariant layer (or function) $\psi: X \to Y$ from an input G-space $X$ to an output G-space $Y$. The input space is the pixel space and we choose the same output space: $Y=X$. So both input and output are the gray-scale image (they might be of different sizes / dimensions.)

The equivariant layer will be $3 \times 3$ filter. We will verify that a random filter is not a rotational equivariant layer.

# random filter

torch.manual_seed(37)

x = torch.randn(1, 1, 33, 33) ** 3
gx = rotate(x, 1)
filter = torch.randn(1, 1, 3, 3)

psi_x = torch.conv2d(x, filter, bias=None, padding=1)
psi_gx = torch.conv2d(gx, filter, bias=None, padding=1)

g_psi_x = rotate(psi_x, 1)

fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(g_psi_x[0, 0].numpy())
axes[0].set_title('$g.\psi(x)$')

axes[1].imshow(psi_gx[0, 0].numpy())
axes[1].set_title('$\psi(g.x)$')
plt.show()

print('Equivariant' if torch.allclose(psi_gx, g_psi_x, atol=TOL, rtol=TOL) else 'Not equivariant!!')

Not equivariant!!

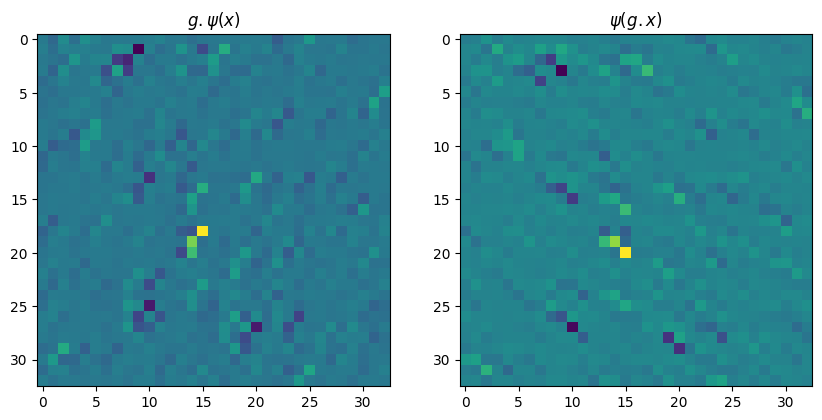
Clearly, if the filter $\psi$ has no constraint on the weights,

\[\psi(gx) \neq g\psi(x)\]

There must be some $C_4$ symmetry boiled in the filter. Let’s first try the isotropic filter where there are 2 trainable weights: one in the middle, the the other in the ring.

# Isotropic filter
# The filter looks like: 
# a, a, a
# a, b, a
# a, a, a

torch.manual_seed(37)

filter = torch.empty(1, 1, 3, 3)
filter[0, 0, 1, 1] = np.random.randn() # middle pixel
mask = torch.ones(3, 3, dtype=torch.bool)
mask[1, 1] = 0
filter[0, 0, mask] = np.random.randn() # ring pixel

# we recycle the previous codes: 
psi_x = torch.conv2d(x, filter, bias=None, padding=1)
psi_gx = torch.conv2d(gx, filter, bias=None, padding=1)

g_psi_x = rotate(psi_x, 1)

fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(g_psi_x[0, 0].numpy())
axes[0].set_title('$g.\psi(x)$')

axes[1].imshow(psi_gx[0, 0].numpy())
axes[1].set_title('$\psi(g.x)$')
plt.show()

print('Equivariant' if torch.allclose(psi_gx, g_psi_x, atol=TOL, rtol=TOL) else 'Not equivariant!!')

Equivariant

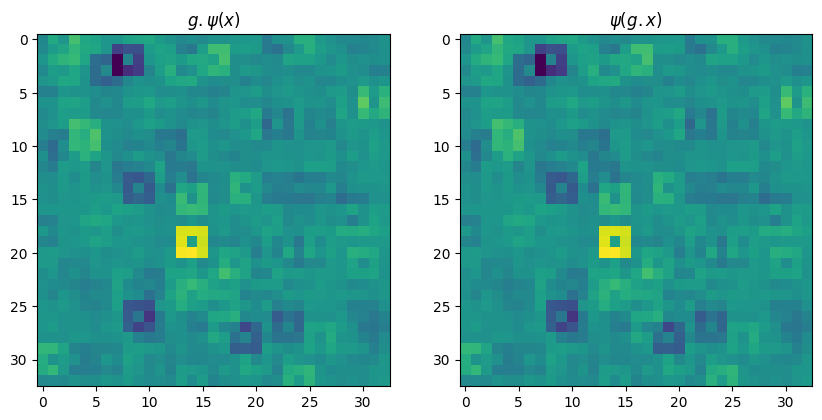
Let’s use this filter to build a equivariant convolution layer:

class IsotropicEConv2d(torch.nn.Module): 

    def __init__(self, in_channels, out_channels, bias=True):
        super(IsotropicEConv2d, self).__init__()
        self.kernel_size = 3
        self.stride = self.dilation = self.padding = 1
        self.in_channels = in_channels
        self.out_channels = out_channels

        # for each filter contains 2 parameters
        # There are total of in_channels x out_channels filters
        self.weight = self.weight = torch.nn.Parameter(torch.empty(self.out_channels, self.in_channels, 2).normal_(mean=0, std=1/np.sqrt(in_channels * out_channels)), requires_grad=True)
        self.bias = torch.nn.Parameter(torch.zeros(out_channels), requires_grad=True) if bias else None

    def build_filter(self): 
        mask = torch.ones(3, 3, dtype=torch.bool)
        filter = torch.zeros(self.out_channels, self.in_channels, 3, 3)
        filter[:, :, mask] = self.weight[:, :, 1].unsqueeze(2).repeat(1, 1, 9)
        filter[:, :, 1, 1] = self.weight[:, :, 0]

        return filter
    
    def forward(self, x):
        _filter = self.build_filter()
        return torch.conv2d(x, _filter, stride=self.stride, padding=self.padding, dilation=self.dilation, bias=self.bias)

Since this layer maps from input space $X$ to input space $X$, so we define the following equivariance checker.

def check_equivariance_XX(layer, x, tol=TOL): 

    layer.eval()

    gx = rotate(x, 1)
    with torch.no_grad():
        psi_x = layer(x)
        psi_gx = layer(gx)
    g_psi_x = rotate(psi_x, 1)

    assert not torch.allclose(psi_x, torch.zeros_like(psi_x), atol=tol, rtol=tol)
    print('Equivariant' if torch.allclose(psi_gx, g_psi_x, atol=tol, rtol=tol) else 'Not equivariant!!')
    return psi_gx, g_psi_x

Let’s check if the IsotropicEConv2d is acturally equivariant:

torch.manual_seed(37)
in_channels = 5
out_channels = 10
batchsize = 16
S = 33

x = torch.randn(batchsize, in_channels, S, S) ** 2
layer = IsotropicEConv2d(in_channels=x.shape[1], out_channels=16, bias=True)
psi_gx, g_psi_x = check_equivariance_XX(layer, x, tol=TOL)

fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(g_psi_x[0, 0].numpy())
axes[0].set_title('$g.\psi(x)$')

axes[1].imshow(psi_gx[0, 0].numpy())
axes[1].set_title('$\psi(g.x)$')
plt.show()

Equivariant

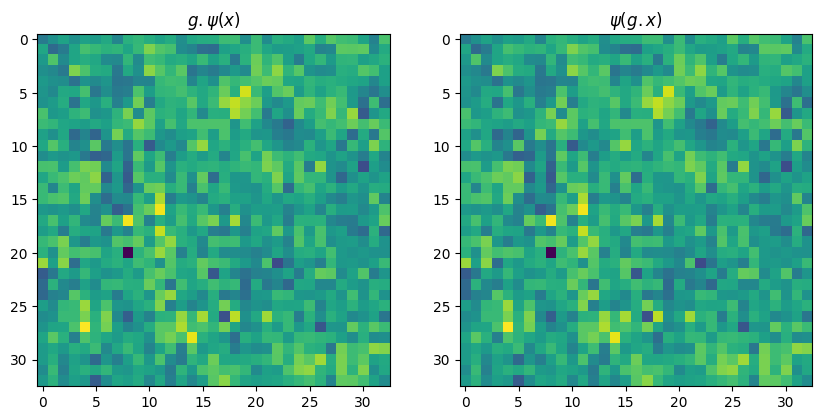
Unfortunately, isotropic filters are not very expressive. Instead, we would like to use more general, unconstrained filters. To do so, we need to rely on group convolution.

Let $X$ be the space of grayscale images, $\psi \in X$ be a filter and $x \in x$ be an input image. The group convolution is

\[[\psi x](t, r) = \sum_{p} \psi((t, r)^{-1}p)x(p) = \sum_{p} \psi(r^{-1}(p - t))x(p)\]

The output of the convolution is not a grayscale image in $X$. It is now a function over the rotational group. The use of the filter $\psi$ in the group convolution maps the input space $X$ into a new larger space $Y$, where $Y$ is the space of all function $y: p_4 \to \mathbf{R}$.

This is the lifting convolution since it maps the space $X$ to the more complex space $Y$. Note that a function $y \in Y$ can be implemented as a 4-channel image, where the ith channel is defined as $y_i(t) = y(y, r=i) \in \mathbf{R}, i \in \{0, 1, 2, 3\}$

In the end of the day, we want to have a network

\[X \to H_1 \to H_2 \to ... \to Y\]

where $X$ is the grayscale image or the 3-channel image space and $H$’s are the group (hidden) space and $Y$ can be a pooled invariant output or equivariant output space.

def rotate_p4(y, r): 
    # y is (..., 4, h, w)
    # r = 0, 1, 2, 3
    
    assert len(y.shape) >= 3
    assert y.shape[-3] == 4
    assert r in [0, 1, 2, 3]

    ry = y.clone()
    # then we just rotate each of the 4 channels
    for i in range(4): ry[:, :, (i + r) % 4, :, :] = rotate(y[:, :, i, :, :], r)
    return ry

See the rotation p4 group by $r = 1$:

# Test the rotation by r = 1
torch.manual_seed(37)
y = torch.randn(1, 1, 4, 33, 33) ** 3
y[0, 0, :, 16, 16] = torch.ones(4)*10


ry = rotate_p4(y, 1)

fig, axes = plt.subplots(1, 4, sharex=True, sharey=True, squeeze=True, figsize=(16, 4))
for i in range(4):
  axes[i].imshow(y[0, 0, i].numpy())
fig.suptitle('Original y')
plt.show()

fig, axes = plt.subplots(1, 4, sharex=True, sharey=True, squeeze=True, figsize=(16, 4))
for i in range(4):
  axes[i].imshow(ry[0, 0, i].numpy())
fig.suptitle('Rotated y')
plt.show()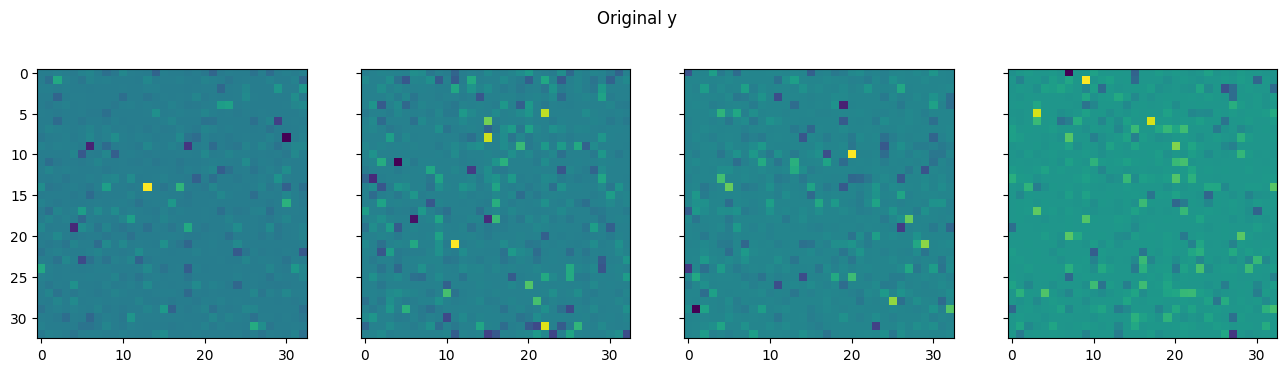

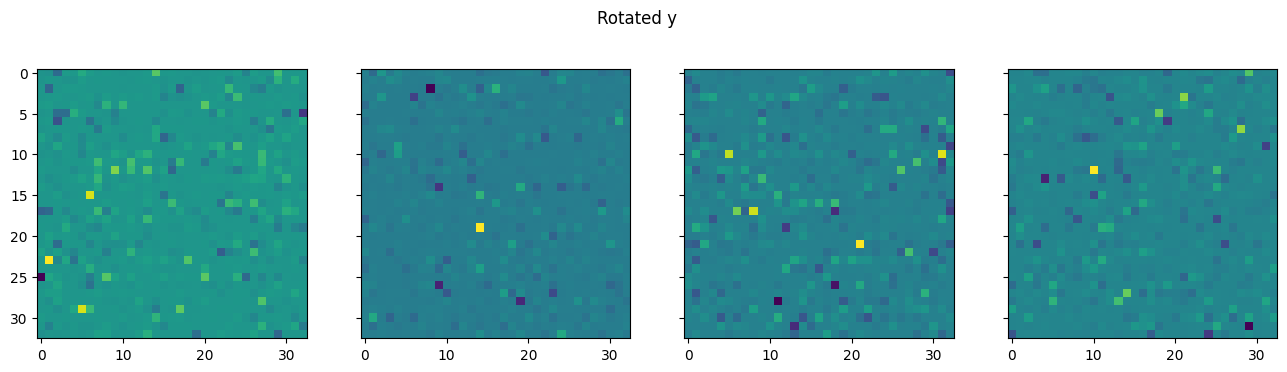
Next, we will build a lifting convoltuion. The input is a grayscale image $x \in X$ and the output is a function $y \in Y$. This can berealized by exploiting the usual convolution using 4 rotated copies of a SINGLE learnable filter. The image is colvolved with each copy independently by stacking 4 copies into a unique filter with 4 output channels.

Finally, a convolutional layer usually includes a bias term. In a normal convolutional network, it is common to share the same bias over all pixels, i.e. the same bias is summed to the features at each pixel. Similarly, when we use a lifting convolution, we share the bias over all pixels but also over all rotations, i.e. over the output channels.

# Lift conv of C4 Group

class LiftingConv2d(torch.nn.Module): 
    
    def __init__(self, in_channels: int, out_channels: int, kernel_size: int, padding: int = 0, bias: bool = True):
        super(LiftingConv2d, self).__init__()
        
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = kernel_size
        self.padding = padding
        self.stride = 1
        self.dilation = 1
        
        # learnable weights for `out_channels x in_channels` different learnable filters, each of shape `kernel_size x kernel_size`
        # later populate the larger C4 filters of shape `out_channels x 4 x in_channels x kernel_size x kernel_size` by rotating 4 times 
        self.weight = torch.nn.Parameter(torch.empty(self.out_channels, 
                                                     self.in_channels, 
                                                     self.kernel_size, 
                                                     self.kernel_size).normal_(mean=0, 
                                                                               std=1/np.sqrt(self.in_channels * self.out_channels)),
                                         requires_grad=True)
        
        self.bias = None
        if bias:
            self.bias = torch.nn.Parameter(torch.randn(self.out_channels), requires_grad=True)
    
    def _build_filter(self) -> torch.Tensor:
        # using the tensors of learnable parameters, build 
        # - the `out_channels x 4 x in_channels x kernel_size x kernel_size` filter
        # - the `out_channels x 4` bias
        _filter = torch.zeros(self.out_channels, 4, self.in_channels, self.kernel_size, self.kernel_size)
        for i in range(4): _filter[:, i, :, :, :] = rotate(self.weight, i)
        
        if self.bias is not None: 
            _bias = einops.repeat(self.bias, 'c -> c g', g=4)
        else: 
            _bias = torch.zeros(self.out_channels, 4)
        
        return _filter, _bias
    
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        
        _filter, _bias = self._build_filter()
        assert _filter.shape == (self.out_channels, 4, self.in_channels, self.kernel_size, self.kernel_size), f'lifting _filter has shape {_filter.shape}'
        assert _bias.shape == (self.out_channels, 4), f'lifting _bias has shape {_bias.shape}'
        
        _filter = einops.rearrange(_filter, 'o c i w h -> (o c) i w h')
        _bias = einops.rearrange(_bias, 'c g -> (c g)')
        
        out = torch.conv2d(x, _filter, stride=self.stride, padding=self.padding, dilation=self.dilation, bias=_bias)
        return einops.rearrange(out, 'b (o c) w h -> b o c w h', c=4)

Since this layer maps from input space $X$ to group space $Y$, so we define the following equivariance checker.

def check_equivariance_XY(layer, x, tol=TOL): 

    layer.eval()

    gx = rotate(x, 1) # rotate in X
    with torch.no_grad():
        psi_x = layer(x)
        psi_gx = layer(gx)
    g_psi_x = rotate_p4(psi_x, 1) # rotate in Y

    assert not torch.allclose(psi_x, torch.zeros_like(psi_x), atol=tol, rtol=tol)
    print('Equivariant' if torch.allclose(psi_gx, g_psi_x, atol=tol, rtol=tol) else 'Not equivariant!!')
    return psi_gx, g_psi_x

Let’s check if the LiftingConv2d is equivariant.

# Let's check if the layer is really equivariant

in_channels = 5
out_channels = 10
kernel_size = 3
batchsize = 6
S = 33

layer = LiftingConv2d(in_channels=in_channels, out_channels=out_channels, kernel_size = kernel_size, padding=1, bias=True)
# layer.to(DEVICE)
layer.eval()

x = torch.randn(batchsize, in_channels, S, S)
psi_gx, g_psi_x = check_equivariance_XY(layer, x)

Equivariant

The lifting convolution is only the first piece of building the $C_4$ equivariant neural network. Remember we are after

\[X \to H_1 \to H_2 \to ... \to Y\]

and lifting convolution is the first “$\to$”, we still need to build equivariant layers from $H_i \to H_j$.

As compared to the usual CNN: $X \to X \to X ... \to Y$.

We will construct the convolution on the OUTPUT from the lifting convolution.

\[[\psi x](t, r) = \sum_{s \in C_4}\sum_{p}[r \psi](p-t, s)x(p, s)\]

So we simply use additional 4-rotated filters for the convolution of the input, i.e. 4 rotated filters for 4 channels from lift convolution. The output of this group convolution is also 4 channels and we can stack this group convolution to build a deep G-CNN.

# GroupConv2d

class GroupConv2d(torch.nn.Module):
    
    def __init__(self, in_channels: int, out_channels: int, kernel_size: int, padding: int = 0, bias: bool = True):
        super(GroupConv2d, self).__init__()
        
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = kernel_size
        self.padding = padding
        self.stride = 1
        self.dilation = 1
        
        self.weight = torch.nn.Parameter(torch.empty(self.out_channels, 
                                                     self.in_channels, 
                                                     4,
                                                     self.kernel_size, 
                                                     self.kernel_size).normal_(mean=0, 
                                                                               std=1/np.sqrt(self.in_channels * self.out_channels)),
                                         requires_grad=True)
        
        self.bias = None
        if bias:
            self.bias = torch.nn.Parameter(torch.randn(self.out_channels), requires_grad=True)
    
    def _build_filter(self) -> torch.Tensor:
        # using the tensors of learnable parameters, build 
        # - the `out_channels x 4 x in_channels x 4 x kernel_size x kernel_size` filter
        # - the `out_channels x 4` bias
        _filter = torch.zeros(self.out_channels, 4, self.in_channels, 4, self.kernel_size, self.kernel_size)
        for i in range(4): _filter[:, i, :, :, :] = rotate_p4(self.weight, i)
        
        if self.bias is not None: 
            _bias = einops.repeat(self.bias, 'c -> c g', g=4)
        else: 
            _bias = torch.zeros(self.out_channels, 4)
        
        return _filter, _bias
    
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        
        _filter, _bias = self._build_filter()
        assert _filter.shape == (self.out_channels, 4, self.in_channels, 4, self.kernel_size, self.kernel_size), f'groupconv _filter has shape {_filter.shape}'
        assert _bias.shape == (self.out_channels, 4), f'groupconv _bias has shape {_bias.shape}'
        
        _filter = einops.rearrange(_filter, 'o c i s w h -> (o c) (i s) w h')
        _bias = einops.rearrange(_bias, 'c g -> (c g)')
        
        # x is `batch_size x in_channels x 4 x W x H`
        x = einops.rearrange(x, 'b i c w h -> b (i c) w h')
        
        out = torch.conv2d(x, _filter, stride=self.stride, padding=self.padding, dilation=self.dilation, bias=_bias)
        return einops.rearrange(out, 'b (o c) w h -> b o c w h', c=4)

Now, GroupConv2d maps from group space $Y$ to the same group space $Y$. We will define another equivariance checker.

def check_equivariance_YY(layer, x, tol=TOL): 

    layer.eval()

    gx = rotate_p4(x, 1) # rotate in Y
    with torch.no_grad():
        psi_x = layer(x)
        psi_gx = layer(gx)
    g_psi_x = rotate_p4(psi_x, 1) # rotate in Y

    assert not torch.allclose(psi_x, torch.zeros_like(psi_x), atol=tol, rtol=tol)
    print('Equivariant' if torch.allclose(psi_gx, g_psi_x, atol=tol, rtol=tol) else 'Not equivariant!!')
    return psi_gx, g_psi_x

And ckeck the equivariance.

# Let's check if the layer is really equivariant
torch.manual_seed(42)

in_channels = 5
out_channels = 10
kernel_size = 3
batchsize = 4
S = 33

layer = GroupConv2d(in_channels=in_channels, out_channels=out_channels, kernel_size = kernel_size, padding=1, bias=True)
layer.eval()

x = torch.randn(batchsize, in_channels, 4, S, S)**2
psi_gx, g_psi_x = check_equivariance_YY(layer, x)

Equivariant

3. Implement A Deep Rotation Equivariant CNN

Fianlly, you can combine the layers you have implemented earlier to build a rotation equivariant CNN. You model will take in input batches of $33 \times 33$ images with a single input channel.

The network performs a first lifting layer with $8$ output channels and is followed by $4$ group convolution with, respectively, $16$, $32$, $64$ and $128$ output channels. All convolutions have kernel size $3$, padding $1$ and stride $1$ and should use the bias. All convolutions are followed by torch.nn.MaxPool3d and torch.nn.ReLU. Note that we use MaxPool3d rather than MaxPool2d since our feature tensors have $5$ dimensions (there is an additional dimension of size $4$). In all pooling layers, we will use a kernel of size $(1, 3, 3)$, a stride of $(1, 2, 2)$ and a padding of $(0, 1, 1)$. This ensures pooling is done only on the spatial dimensions, while the rotational dimension is preserved. The last pooling layer, however, will also pool over the rotational dimension so it will use a kernel of size $(4, 3, 3)$, stride $(1, 1, 1)$ and padding $(0, 0, 0)$.

Finally, the features extracted from the convolutional network are used in a linear layer to classify the input in $10$ classes.

# Equivariant Networks

# Lifting Layers: X -> Y over p4
# GroupConv Layers: Y -> Y over p4

# So the idea is to have a lifting layer followed by groupconv layers and non linearities

# to make it invariant, make sure to use c4_pooling at the end
class C4CNN(torch.nn.Module): 
    
    def __init__(self, n_classes=10): 
        super(C4CNN, self).__init__()
        channels = [8, 16, 32, 64, 128]
        self.n_classes = n_classes
        
        self.liftingconv = LiftingConv2d(in_channels=1, out_channels=8, kernel_size=3, padding=1, bias=True)
        layers = []
        for i in range(4): 
            layers.append(GroupConv2d(in_channels=channels[i], out_channels=channels[i + 1], kernel_size=3, padding=1, bias=True))
            layers.append(torch.nn.ReLU())
            
            if i != 3: layers.append(torch.nn.MaxPool3d(kernel_size=(1, 3, 3), stride=(1, 2, 2), padding=(0, 1, 1)))
        self.groupconv_encoder = torch.nn.Sequential(*layers)
        self.flatten = torch.nn.Flatten(start_dim=1)
        self.head = torch.nn.Sequential(torch.nn.Linear(3200, 256), 
                                        torch.nn.ReLU(),
                                        torch.nn.Linear(256, 32), 
                                        torch.nn.ReLU(), 
                                        torch.nn.Linear(32, n_classes))
    
    def _c4_pool(self, x: torch.Tensor) -> torch.Tensor: 
        assert len(x.shape) == 5 # batch, channel, group, height, weight
        assert x.shape[2] == 4

        x_pre_pool = torch.concat([rotate(x, i) for i in range(4)], dim=2)
        x_pool = x_pre_pool.mean(2)
        return x_pool
    
    def forward(self, x: torch.Tensor): 
        lifted_x = self.liftingconv(x)
        gp_encoded_x = self.groupconv_encoder(lifted_x) # batch x channel x group x width x height

        # Before pooling, the network is equivariant and after pooling, the model is invariant
        # however, the hidden features are still equivariant 
        pooled_x = self._c4_pool(gp_encoded_x) # batch x channel x 1 x width x height
        flattened_x = self.flatten(pooled_x) # batch x 3200
        return self.head(flattened_x)

So C4CNN is invariant to $C_4$ rotation, meaning that it can recognize an image even though it’s rotated in $C_4$. the C4CNN, though invariant, it contains a lot to hidden features that are equivariant. In other words:

Rotated image -> rotated features -> rotated features -> … -> invariant output

Allowing the equivariant hidden features make the model more powerful and data efficient because the model is already symmetry-restricted.

Let’s check if the C4CNN is invariant.

net = C4CNN()

torch.manual_seed(37)
x = torch.randn(5, 1, 33, 33)
y = net(x)

assert y.shape == (5, 10) # batch x n_classes

# Let's check if the model is invariant!
gx = rotate(x, 1)
gy = net(gx)
assert torch.allclose(y, gy, atol=TOL, rtol=TOL)

4. Compare CNN to GCNN on rotated MNIST dataset

After buidling the C4CNN as $C_4$-invariant model with $C_4$-equivariant features, we want to compare it with typical CNN on the rotated MNIST dataset.

# dataset
# https://zenodo.org/record/3670627/files/mnist_rotation_new.zip?download=1
class MnistRotDataset(Dataset):
    
    def __init__(self, mode, transform=None):
        assert mode in ['train', 'test']
            
        if mode == 'train': file = './mnist_rotation_new/mnist_all_rotation_normalized_float_train_valid.amat'
        else: file = './mnist_rotation_new/mnist_all_rotation_normalized_float_test.amat'
        
        self.transform = transform

        data = np.loadtxt(file, delimiter=' ')
        
        self.labels = data[:, -1].astype(np.int64)
        self.num_samples = len(self.labels)    
        self.images = data[:, :-1].reshape(-1, 28, 28).astype(np.float32)

        # images in MNIST are only 28x28
        # we pad them to have shape 33 x 33
        self.images = np.pad(self.images, pad_width=((0,0), (2, 3), (2, 3)), mode='edge')

        assert self.images.shape == (self.labels.shape[0], 33, 33)
    
    def __getitem__(self, index):
        image, label = self.images[index], self.labels[index]
        image = Image.fromarray(image)
        if self.transform is not None:
            image = self.transform(image)
        return image, label
    
    def __len__(self):
        return len(self.labels)


train_set = MnistRotDataset('train', ToTensor())
test_set = MnistRotDataset('test', ToTensor())

We define functions to train and test models, which is typical pytorch forward pass with/without gradients.

def train_model(model: torch.nn.Module, nepoch: int=30):
    train_loader = torch.utils.data.DataLoader(train_set, batch_size=64)
    loss_function = torch.nn.CrossEntropyLoss()
    optimizer = torch.optim.AdamW(model.parameters(), lr=5e-5, weight_decay=1e-5)
    
    model.train()

    for epoch in tqdm(range(nepoch + 1)):
        for i, (x, t) in enumerate(train_loader):

            # x, t = x.to(DEVICE), t.to(DEVICE)
            y = model(x)

            loss = loss_function(y, t)
            loss.backward()
            optimizer.step()
            optimizer.zero_grad()
    
    return model


def test_model(model: torch.nn.Module):
    test_loader = torch.utils.data.DataLoader(test_set, batch_size=64)
    total = 0
    correct = 0
    with torch.no_grad():
        model.eval()
        for i, (x, t) in tqdm(enumerate(test_loader)):
            x = x.to(DEVICE)
            t = t.to(DEVICE)
          
            y = model(x)

            _, prediction = torch.max(y.data, 1)
            total += t.shape[0]
            correct += (prediction == t).sum().item()
    
    accuracy = correct/total*100.
    return accuracy

Next, we define a CNN model similar to C4CNN by recycling the code.

# Build a normal CNN 
class CNN(torch.nn.Module):

    def __init__(self, n_classes=10):
        super(CNN, self).__init__()
        
        channels = [8, 16, 32, 64, 128]
        self.first_conv = torch.nn.Conv2d(in_channels=1, out_channels=8, kernel_size=3)

        layers = []
        for i in range(4):
            layers.append(torch.nn.Conv2d(in_channels=channels[i], out_channels=channels[i + 1], kernel_size=3))
            layers.append(torch.nn.ReLU())
            if i != 3: layers.append(torch.nn.MaxPool2d(kernel_size=(3, 3), stride=(2, 2), padding=(1, 1)))
        self.convs = torch.nn.Sequential(*layers)
        self.flatten = torch.nn.Flatten(start_dim=1)
        self.head = torch.nn.Sequential(torch.nn.Linear(128, 32), 
                                        torch.nn.ReLU(), 
                                        torch.nn.Linear(32, n_classes))

    def forward(self, x):

        x = self.first_conv(x)
        # x = torch.nn.functional.layer_norm(x, x.shape[-3:])
        x = torch.nn.functional.relu(x)

        x = self.convs(x)
        x = self.flatten(x)

        # apply average pooling over remaining spatial dimensions
        # x = torch.nn.functional.adaptive_avg_pool2d(x, 1).squeeze()
        x = self.head(x)
        return x

Let’s finally get the models trained and report the accuracies.

# training and keep the stats

print('Training C4CNN')
c4cnn = train_model(C4CNN(), nepoch=50)

print('Training CNN')
cnn = train_model(CNN(), nepoch=50)


acc_c4cnn = test_model(c4cnn)
acc_cnn = test_model(cnn)

print(f'C4CNN Test Accuracy: {acc_c4cnn :.3f}')
print(f'CNN Test Accuracy: {acc_cnn :.3f}')

C4CNN Test Accuracy: 91.744
CNN Test Accuracy: 82.134

5. Final Note

The performance of C4CNN is significantly higher. I also did 25 repeated runs and C4CNN and CNN averaged 92% and 81% in accuracy. However, C4CNN took about 5x more time to train. Considering the (maybe) 4x data one needs to augment, this might not be beneficial in this case and also natural equivariance shows up in the trained filters.

However, equivariance makes a lot difference in the continuous group where one cannot just rotate the filters to achieve equivariance.